Vector: características y propiedades, elementos, tipos, ejemplos

Los vectores son entidades matemáticas que poseen una magnitud –positiva-, generalmente acompañada de una unidad de medida, además de dirección y sentido. Tales características son muy apropiadas para describir cantidades físicas como velocidad, fuerza, aceleración y muchas más.

Con los vectores es posible realizar operaciones como suma, resta y productos. La división no está definida para los vectores y en cuanto al producto, hay tres clases que describiremos más adelante: producto escalar o punto, producto vectorial o cruz y producto de un escalar por un vector.

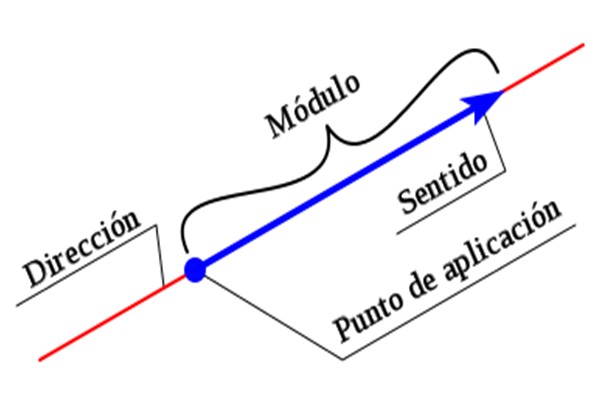
Para describir completamente un vector, es preciso indicar todas sus características. La magnitud o módulo es un valor numérico acompañado de una unidad, mientras que la dirección y el sentido se establecen con ayuda de un sistema de coordenadas.

Veamos un ejemplo: supongamos que un avión vuela de una ciudad a otra a razón de 850 km/h en dirección NE. Aquí tenemos un vector completamente especificado, pues se dispone de la magnitud: 850 km/h, mientras que la dirección y el sentido son NE.

Los vectores suelen representarse gráficamente mediante segmentos de recta orientados, cuya longitud es proporcional a la magnitud.

Mientras que para especificar la dirección y el sentido se requiere de una línea de referencia que suele ser el eje horizontal, aunque también puede tomarse el norte como referencia, tal es el caso de la velocidad del avión:

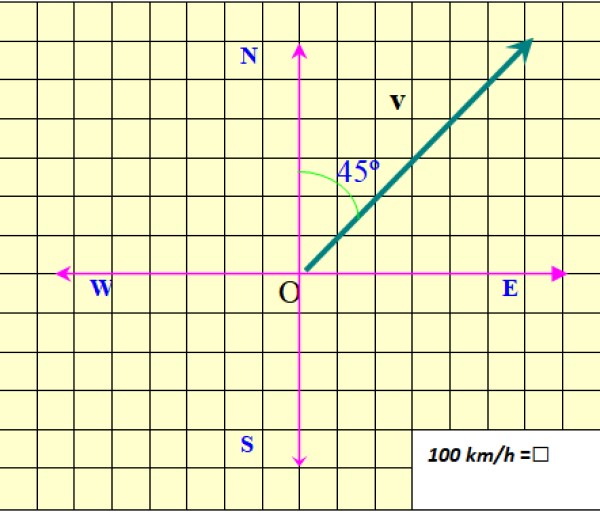
La figura muestra el vector velocidad del avión, al que se denota comov en letra negrita, para distinguirlo de una cantidad escalar, que solamente requiere de un valor numérico y alguna unidad para quedar especificada.

Índice del artículo

• 1 Elementos de un vector
  • 1.1 Componentes rectangulares de un vector
• 2 Tipos
  • 2.1 Vectores unitarios ortogonales
• 3 Suma de vectores
  • 3.1 Propiedades de la suma de vectores
• 4 Ejemplos de vectores
• 5 Otras operaciones entre vectores
  • 5.1 Producto de un escalar por un vector
  • 5.2 Producto escalar o producto punto entre vectores
  • 5.3 Producto cruz o producto vectorial entre vectores
• 6 Ejercicios resueltos
  • 6.1 – Ejercicio 1
  • 6.2 – Ejercicio 2
• 7 Referencias

Elementos de un vector

Tal como hemos dicho, los elementos del vector son:

-Magnitud o módulo, algunas veces también llamado valor absoluto o norma del vector.

-Dirección

-Sentido

En el ejemplo de la figura 2, el módulo de v es 850 km/h. El módulo se denota como v sin negritas, o como |v|, donde las barras representan el valor absoluto.

La dirección de v se especifica respecto al Norte. En este caso es 45º al Norte del Este (45º NE). Finalmente la punta de la flecha informa acerca del sentido de v.

En este ejemplo se ha dibujado el origen del vector coincidiendo con el origen O del sistema de coordenadas, a esto se le conoce como vector ligado. En cambio, si el origen del vector no coincide con el del sistema de referencia, se dice que es un vector libre.

Debe observarse que para precisar completamente el vector, hay que señalar estos tres elementos, de lo contrario la descripción del vector sería incompleta.

Componentes rectangulares de un vector

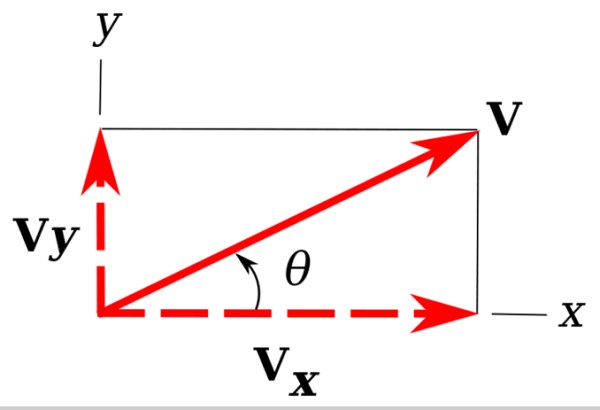
En la imagen tenemos de vuelta nuestro vector de ejemplo v, que se encuentra en el plano xy.

Es fácil advertir que las proyecciones de v sobre los ejes coordenados x e y determinan un triángulo rectángulo. Dichas proyecciones son v_y y v_x y se denominan componentes rectangulares de v.

Una forma de denotar a v mediante sus componentes rectangulares es así: v = x, v_y>. Se usan estos corchetes en vez de paréntesis para enfatizar el hecho de que se trata de un vector y no de un punto, ya que en este caso se usarían paréntesis.

Si el vector se encuentra en el espacio tridimensional, hace falta una componente más, de manera que:

v = x, v_y, v_z>

Conociendo las componentes rectangulares se calcula la magnitud del vector, equivalente a encontrar la hipotenusa del triángulo rectángulo cuyos catetos son v_x y v_y,. Mediante el teorema de Pitágoras se sigue que:

|v|² = (v_x)² +  (v_y)²

Forma polar de un vector

Cuando se conocen la magnitud del vector |v| y el ángulo θ que este forma con el eje de referencia, por lo general el eje horizontal, el vector queda igualmente especificado. Se dice entonces que el vector está expresado en forma polar.

Las componentes rectangulares en este caso se calculan fácilmente:

v_x = |v|.cos θ

v_y = |v|.sen θ

De acuerdo a lo anterior, las componentes rectangulares del vector velocidad v del avión serían:

v_x = 850 . cos 45º km/h= 601.04 km/h

v_y = 850 . sen 45º km/h= 601.04 km/h

Tipos

Existen diversos tipos de vectores. Hay vectores de velocidad, posición, desplazamiento, fuerza, campo eléctrico, cantidad de movimiento y muchos más. Como ya hemos dicho, en física hay una gran cantidad de magnitudes vectoriales.

En cuanto a vectores que poseen determinadas características, podemos mencionar los siguientes tipos de vectores:

-Nulos: se trata de vectores cuya magnitud es 0 y que se denotan como 0. Recuérdese que la letra negrita simboliza las tres características fundamentales de un vector, mientras que la letra normal representa únicamente al módulo.

Por ejemplo sobre un cuerpo en equilibrio estático, la sumatoria de fuerzas debe ser un vector nulo.

–Libres y ligados: los vectores libres son aquellos cuyos puntos de origen y de llegada son cualquier par de puntos del plano o del espacio, a diferencia de los vectores ligados, cuyo origen coincide con el del sistema de referencia empleado para describirlos.

El par o momento producido por un par de fuerzas es un buen ejemplo de vector libre, ya que el par no se aplica a algún punto en particular.

–Equipolentes: son dos vectores libres que comparten idénticas características. Por lo tanto tienen igual magnitud, dirección y sentido.

–Coplanares o coplanarios: vectores que pertenecen a un mismo plano.

–Opuestos: vectores con igual magnitud y dirección, pero sentidos opuestos. El vector opuesto a un vector v es el vector –v y la suma de ambos es el vector nulo: v + (-v) = 0.

–Concurrentes: vectores cuyas líneas de acción pasan todas por un mismo punto.

–Deslizantes: son aquellos vectores cuyo punto de aplicación puede deslizar a lo largo de una recta en particular.

–Colineales: vectores que se ubican sobre una misma recta.

–Unitarios: aquellos vectores cuyo módulo es 1.

Vectores unitarios ortogonales

Existe un tipo de vector muy útil en física llamado vector unitario ortogonal. El vector unitario ortogonal tiene módulo igual a 1 y las unidades pueden ser cualesquiera, por ejemplo las de velocidad, posición, fuerza u otras.

Existe un conjunto de vectores especiales que ayudan a representar fácilmente  a otros vectores y a realizar operaciones con ellos: son los vectores unitarios ortogonales i, j y k, unitarios y perpendiculares entre sí.

En dos dimensiones, estos vectores están dirigidos a lo largo del sentido positivo tanto del eje x como del eje y. Y en tres dimensiones se añade un vector unitario en dirección al eje z positivo. Se representan de la siguiente manera:

i = 1, 0,0>

j = 0,1,0>

k = 0,0,1>

Un vector se puede representar mediante los vectores unitarios i, j y k como sigue:

v = v_xi + v_yj + v_zk

Por ejemplo el vector velocidad v de los ejemplos anteriores se puede escribir como:

v = 601.04 i + 601.04 j km/h

La componente en k no es necesaria, ya que este vector está en el plano.

Suma de vectores

La suma de vectores aparece con mucha frecuencia en diversas situaciones, por ejemplo cuando se desea encontrar la fuerza resultante sobre un objeto que es afectado por diversas fuerzas. Para comenzar supongamos que se tienen dos vectores libres u y v sobre el plano, tal como lo muestra la siguiente figura la izquierda:

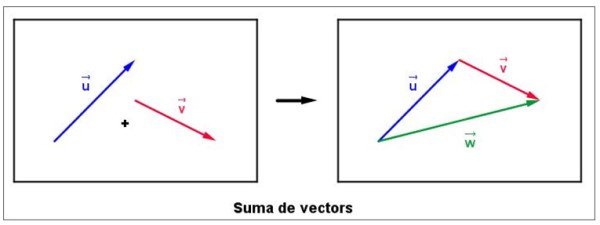
De inmediato se traslada cuidadosamente al vector v, sin modificar su magnitud, dirección ni sentido, para que se origen coincida con el extremo de u.

El vector suma se llama w y se dibuja partiendo de u terminando en v, de acuerdo a la figura derecha. Es importante destacar que la magnitud del vector w no necesariamente es la suma de las magnitudes de v y u.

Si se reflexiona cuidadosamente al respecto, la única ocasión en que la magnitud del vector resultante es la suma de las magnitudes de los sumandos, es cuando ambos sumandos están en la misma dirección y tienen el mismo sentido.

¿Y qué sucede si los vectores no son libres? También es muy sencillo sumarlos. La manera de hacerlo es sumando componente a componente, o método analítico.

Como ejemplo consideremos los vectores de la siguiente figura, lo primero es expresarlos de alguna de las formas cartesianas explicadas previamente:

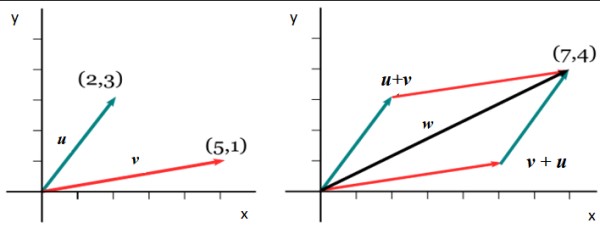
v = 5,1>

u = 2,3>

Para obtener la componente en x del vector suma w, se suman las respectivas componentes en x de v y u: w_x = 5+2 = 7. Y para obtener w_yse sigue un procedimiento análogo: w_y = 1+3. Por lo tanto:

u = 7,4>

Propiedades de la suma de vectores

-La suma de dos o más vectores da como resultado otro vector.

-Es conmutativa, el orden de los sumandos no altera la suma, de tal manera que:

u + v = v + u

–El elemento neutro de la suma de vectores es el vector nulo: v + 0 = v

–La resta de dos vectores se define como la suma del opuesto: v – u = v + (-u)

Ejemplos de vectores

Como hemos dicho, hay numerosas cantidades vectoriales en física. Entre las más conocidas están:

-Posición

-Desplazamiento

-Velocidad media y velocidad instantánea

-Aceleración

-Fuerza

-Cantidad de movimiento

-Torque o momento de una fuerza

-Impulso

-Campo eléctrico

-Campo magnético

-Momento magnético

Por otra parte no son vectores sino escalares:

-Tiempo

-Masa

-Temperatura

-Volumen

-Densidad

-Trabajo mecánico

-Energía

-Calor

-Potencia

-Voltaje

-Corriente eléctrica

Otras operaciones entre vectores

Además de la suma y la resta de vectores, hay otras tres operaciones entre vectores muy importantes, porque dan lugar a nuevas magnitudes físicas muy importantes:

-Producto de un escalar por un vector.

-El producto escalar o producto punto entre  vectores

-Y el producto cruz o vectorial entre dos vectores.

Producto de un escalar por un vector

Consideremos la segunda ley de Newton, que afirma que la fuerza F y la aceleración a son proporcionales. La constante de proporcionalidad es la masa m del objeto, por lo tanto:

F = m.a

La masa es un escalar; por su parte la fuerza y la aceleración son vectores. Como la fuerza se obtiene multiplicando la masa por la aceleración, es el resultado del producto de un escalar por un vector.

Este tipo de producto siempre da como resultado un vector. Acá otro ejemplo: la cantidad de movimiento. Sea P el vector cantidad de movimiento, v el vector velocidad y como siempre, m es la masa:

P = m.v

Producto escalar o producto punto entre vectores

Hemos colocado al trabajo mecánico en la lista de magnitudes que no son vectores. Sin embargo el trabajo en física es el resultado de una operación entre vectores llamada producto escalar, producto interior o producto punto.

Sean los vectores v y u, se define el producto punto o escalar entre ellos como:

v∙u =|v| ∙ |u |.cos θ

Siendo θ el ángulo entre ambos. De la ecuación mostrada se deduce de inmediato que el resultado del producto punto es un escalar y también que si ambos vectores son perpendiculares, su producto escalar es 0.

De vuelta al trabajo mecánico W, este es el producto escalar entre el vector fuerza F y el vector desplazamiento ℓ.

W = F∙ℓ                  

Cuando se dispone de los vectores en términos de sus componentes, el producto punto también es muy sencillo de calcular. Si v = x, v_y, v_z >y u = x, u_y, u_z >, el producto punto entre ambos es:

v∙u = v_x u_x + v_y u_y + v_z u_z

El producto punto entre vectores es conmutativo, por lo tanto:

v∙u = u∙v

Producto cruz o producto vectorial entre vectores

Si v y u son nuestros dos vectores de ejemplo, se define el producto vectorial como:

v x u = w

De inmediato se sigue que el producto cruz da como resultado un vector, cuyo módulo se define como:

|v x u| =|v| . |u|. sen θ

Donde θ es el ángulo entre los vectores.

El producto cruz no es conmutativo, por lo tanto v x u ≠ u x v. De hecho v x u = – (u x v).

Si los dos vectores de ejemplo se expresan en términos de los vectores unitarios, el cálculo del producto vectorial se facilita:

v = v_xi + v_yj + v_zk

u = u_xi + u_yj + u_zk

Productos cruz entre vectores unitarios

El producto cruz entre vectores unitarios idénticos es nulo, ya que el ángulo entre ellos es 0º. Pero entre vectores unitarios diferentes, el ángulo entre ellos es 90º y sen 90º = 1.

El siguiente esquema ayuda a encontrar estos productos. En sentido de la flecha tiene sentido positivo y en sentido contrario negativo:

i x j = k, j x k = i; k x i = j; j x i = -k; k x j = -i; i x k = -j

Aplicando la propiedad distributiva, que sigue siendo válida para los productos entre vectores más las propiedades de los vectores unitarios, se tiene:

vx u = (v_xi + v_yj + v_zk) x (u_xi + u_yj + u_zk) =  

= (v_yu_z − v_zu_y )i + (v_zu_x − v_xu_z )j + (v_xu_y − v_yu_x )k

Ejercicios resueltos

– Ejercicio 1

Dados los vectores:

v = -5 i + 4j + 1 k

u = 2 i -3 j + 7k

¿Cuál debe ser el vector w para que la suma v + u + w resulte 6 i +8 j -10k?

Solución

-5 i + 4j + 1 k

2 i -3 j + 7k

 w_xi + w_yj + w_zk  +

—————————-

6i + 8 j -10 k

Por lo tanto se debe cumplir que:

-5 +2 + w_x = 6 → w_x = 9

4-3 + w_y =  8→ w_y = 7

1+7 + w_z =  -10 → w_z = -18

La respuesta es: w = 9 i +7 j – 18k

– Ejercicio 2

¿Cuál es el ángulo entre los vectores v y u del ejercicio 1?

Solución

Usaremos el producto escalar. De la definición tenemos:

cos θ = v∙u / |v| ∙ |u|

v∙u= -10 -12+7 = -15

|v|=√(-5)² +4² +1²=√42 = 6.48

|u|=√2² +(-3)² +7²=√62 = 7.87 

Sustituyendo estos valores:

cos θ = -15 / 6.48 x 7.87= -0.2941→ θ = 107.1 º

Referencias

1. Figueroa, D. (2005). Serie: Física para Ciencias e Ingeniería. Volumen 1. Cinemática. Editado por Douglas Figueroa (USB).
2. Giancoli, D.  2006. Physics: Principles with Applications. 6th. Ed Prentice Hall.
3. Rex, A. 2011. Fundamentos de Física. Pearson.
4. Sears, Zemansky. 2016. University Physics with Modern Physics. 14th. Ed. Volume 1.
5. Serway, R., Jewett, J. 2008. Física para Ciencias e Ingeniería. Volumen 1. 7ma. Ed. Cengage Learning.