Física
2020-01-24T14:31:19+01:00

Base ortonormal: propiedades, ejemplos y ejercicios

---

Una base ortonormal se forma con vectores perpendiculares entre sí y cuyo módulo además vale 1 (vectores unitarios). Recordemos que una base B en un espacio vectorial V, se define como un conjunto de vectores linealmente independientes capaces de generar dicho espacio.

A su vez un espacio vectorial es una entidad matemática abstracta entre cuyos elementos están los vectores, generalmente asociados a magnitudes físicas como la velocidad, la fuerza y el desplazamiento o también a matrices, polinomios y funciones.

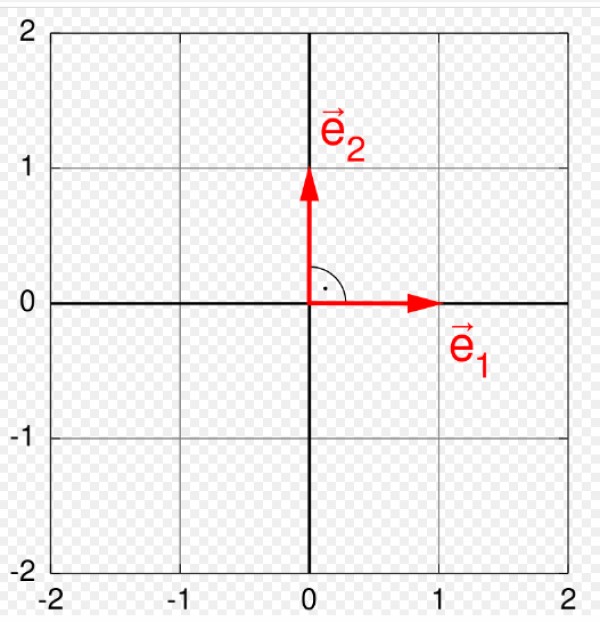
Los vectores tienen tres elementos distintivos: magnitud o módulo, dirección y sentido. Una base ortonormal es especialmente útil para representarlos y operar con ellos, pues cualquier vector que pertenezca a cierto espacio vectorial V, se puede escribir como una combinación lineal de los vectores que forman la base ortonormal.

De esta forma se ejecutan analíticamente las operaciones entre vectores, tales como suma, resta y los distintos tipos de productos definidos en dicho espacio.

Entre las bases más utilizadas de la física está la base formada por los vectores unitarios i, j y k que representan las tres direcciones distintivas del espacio tridimensional: alto, ancho y profundidad. Estos vectores también se conocen con el nombre de vectores canónicos unitarios.

Si en cambio se trabajan los vectores en un plano, bastaría con dos de estas tres componentes, mientras que para los vectores unidimensionales se requiere solo una.

Índice del artículo

• 1 Propiedades de las bases
• 2 Ejemplos de bases
  • 2.1 La base canónica en ℜ n
  • 2.2 La base canónica en ℜ3
  • 2.3 Otras bases ortonormales en ℜ3
• 3 Ejercicios resueltos
  • 3.1 – Ejercicio 1
  • 3.2 – Ejercicio 2
• 4 Referencias

Propiedades de las bases

1- Una base B es el conjunto más pequeño posible de vectores que generan el espacio vectorial V.

2- Los elementos de B son linealmente independientes.

3- Cualquier base B de un espacio vectorial V, permite expresar todos los vectores de V como combinación lineal de ella y esta forma es única para cada vector. Por ello a B se la conoce también como sistema generador.

4- Un mismo espacio vectorial V puede tener diferentes bases.

Ejemplos de bases

A continuación varios ejemplos de bases ortonormales y bases en general:

La base canónica en ℜ ⁿ

También llamada base natural o base estándar de ℜ ⁿ, donde ℜ ⁿ es el espacio n-dimensional, por ejemplo el espacio tridimensional es ℜ ³. Al valor de n se le denomina dimensión del espacio vectorial y se denota como dim (V).

Todos los vectores que pertenecen a  ℜ ⁿ se representan mediante n-adas ordenadas. Para el espacio ℜⁿ, la base canónica es:

e₁ = 1,0,. . . ,0>; e₂ = 0,1,. . . ,0>; …….. e_n = 0,0,. . . ,1>

En este ejemplo hemos utilizado la notación con corchetes o “brackets” y negritas para los vectores unitarios e₁, e₂, e₃…

La base canónica en ℜ³

Los familiares vectores i, j y k admiten esta misma representación y basta con ellos tres para representar los vectores en ℜ ³:

i = 1,0,0 >; j = 0,1,0 >;  k = 0,0,1 >

Significa que la base se puede expresar así:

B = {1,0,0 >; 0,1,0 >;  0,0,1 >}

Para verificar que son linealmente independientes, el determinante formado con ellos vectores es no nulo y además igual a 1:

También debe ser posible escribir cualquier vector que pertenezca a ℜ ³ como combinación lineal de ellos. Por ejemplo, una fuerza cuyas componentes rectangulares son F_x = 4 N, F_y = -7 N y F_z= 0 N quedaría escrita en forma vectorial así:

F = 4,-7,0 > N = 4i -7j + 0k N.

Por lo tanto i, j y k conforman un sistema generador de ℜ ³.

Otras bases ortonormales en ℜ³

La base estándar descrita en el apartado anterior no es la única base ortonormal en ℜ³. Aquí tenemos por ejemplo las bases:

B₁ = {; - sen θ, cos θ,0 >;  0,0,1 >}

B₂ = {3/5, 4/5,0 >; - 4/5, 3/5,0 >;  0,0,1 >}

Se puede demostrar que estas bases son ortonormales, para ello recordemos las condiciones que debe cumplir:

-Los vectores que forman la base deben ser ortogonales entre sí.

-Cada uno de ellos debe ser unitario.

Podemos verificarlo sabiendo que el determinante formado por ellos debe ser no nulo e igual a 1.

La base B₁ es precisamente la de coordenadas cilíndricas ρ, φ y z, otra manera de expresar vectores en el espacio.

Ejercicios resueltos

– Ejercicio 1

Demostrar que la base B = {3/5, 4/5,0 >; - 4/5, 3/5,0 >;  0,0,1 >} es ortonormal.

Solución

Para demostrar que los vectores son perpendiculares entre sí, utilizaremos el producto escalar, también llamado interno o producto punto de dos vectores.

Sean dos vectores cualesquiera u y v, su producto escalar está definido mediante:

u • v = u.v. cosθ

Para distinguir los vectores de sus módulos utilizaremos negritas para los primeros y letras normales para los segundos. θ es el ángulo entre u y v, por lo tanto si son perpendiculares, significa que θ = 90º y el producto escalar es nulo.

Alternativamente, si los vectores están dados en términos de sus componentes: u = x, u_y,u_z > y v = x, v_y,v_z >, el producto escalar de ambos, que es conmutativo, se calcula de esta forma:

 u • v = u_x .v_x + u_y .v_y + u_z .v_z

De esta manera, los productos escalares entre cada par de vectores son, respectivamente:

i) 3/5, 4/5,0 > • - 4/5, 3/5,0 > = (3/5).(-4/5) + (4/5).((3/5) + 0.0 = (-12/25) + (12/25) = 0

ii) 3/5, 4/5,0 > • 0, 0,1 > = 0

iii) - 4/5, 3/5,0 > • 0, 0,1 > = 0

Para la segunda condición se calcula el módulo de cada vector, el cual se obtiene mediante:

│u │= √ (u_x² + u_y² + u_z²)

Así, los módulos de cada vector son:

│3/5, 4/5,0 >│=√ [(3/5)² + (4/5)² + 0²)] = √[(9/25) + (16/25)] =√(25/25) = 1

│-4/5, 3/5,0 >│=√ [(-4/5)² + (3/5)² + 0²)] = √[(16/25) + (9/25)] =√(25/25) = 1

│0, 0,1 >│=√ [0² + 0² + 1²)] = 1

Por lo tanto los tres son vectores unitarios. Finalmente, el determinante que forman es no nulo e igual a 1:

– Ejercicio 2

Escribir las coordenadas del vector w = 2, 3,1 > en términos de la base anterior.

Solución

Para hacerlo se usa el siguiente teorema:

Sea B = {v₁, v₂, v₃, … v_n} una base ortonormal en el espacio V con producto interno, el vector w se representa mediante B de la siguiente forma:

w = w•v₁>v₁ + w•v₂>v₂ +w•v₃>v₃ +…w•v_n>v_n

Esto significa que podemos escribir el vector en la base B, mediante los coeficientes w•v₁>, w•v₂>, … w•v_n>, para lo cual hay que calcular los productos escalares indicados:

2, 3,1 > • 3/5, 4/5,0 > = (2).(3/5) + (3).(4/5) + 1.0 = (6/5) + (12/5) = 18/5

2, 3,1 > • - 4/5, 3/5,0 > = (2).(-4/5) + (3).(3/5) + 1.0 = (-8/5) + (9/5) = 1/5

2, 3,1 > • 0,0,1> = 1

Con los productos escalares obtenidos se construye una matriz, denominada matriz de coordenadas de w.

Por lo tanto las coordenadas del vector w en la base B se expresan mediante:

[w]_B= [(18/5); (1/5); 1]

La matriz de coordenadas no es el vector, puesto que un vector no es lo mismo que sus coordenadas. Estas solamente son un conjunto de números que sirven para expresar al vector en una base dada, no el vector como tal. Además dependen de la base seleccionada.

Por último, siguiendo el teorema, el vector w quedaría expresado así:

 w = (18/5) v₁ + (1/5) v₂ + v₃

Con: v₁ = 3/5, 4/5,0 >; v₂ = - 4/5, 3/5,0 >; v₃ =  0,0,1 >}, es decir, los vectores de la base B.

Referencias

1. Larson, R. Fundamentos de Álgebra Lineal. 6ta. Edición. Cengage Learning.
2. Larson, R. 2006. Cálculo. 7ma. Edición. Volumen 2. McGraw Hill.
3. Salas, J. Algebra Lineal. Tema 10. Bases ortonormales. Recuperado de: ocw.uc3m.es.
4. Universidad de Sevilla. Coordenadas cilíndricas. Base vectorial. Recuperado de: laplace.us.es.
5. Wikipedia. Base ortonormal. Recuperado de: es.wikipedia.org.