Sucesiones cuadráticas: ejemplos, regla y ejercicios resueltos

Las sucesiones cuadráticas, en términos matemáticos, consisten en secuencias de números que siguen una cierta regla aritmética. Es interesante conocer esta regla para determinar cualquiera de los términos de una sucesión.

Una manera de lograrlo es determinar la diferencia entre dos términos sucesivos y ver si el valor obtenido se repite siempre. Cuando es así, se dice que se trata de una sucesión regular.

Pero si no se repite, entonces se puede probar a examinar la diferencia entre las diferencias y ver si este valor es constante. De ser así, entonces se trata de una sucesión cuadrática. 

Índice del artículo

• 1 Ejemplos de sucesiones regulares y sucesiones cuadráticas
  • 1.1 Ejemplo de sucesión regular
  • 1.2 Ejemplo de sucesión no regular y cuadrática
• 2 Regla general para construir una sucesión cuadrática
  • 2.1 Diferencia entre dos términos consecutivos de una sucesión cuadrática
• 3 Ejercicios resueltos de sucesiones cuadráticas
  • 3.1 Ejercicio 1
  • 3.2 Ejercicio 2
  • 3.3 Ejercicio 3
• 4 Referencias

Ejemplos de sucesiones regulares y sucesiones cuadráticas

Los siguientes ejemplos ayudan a clarificar lo explicado hasta ahora:

Ejemplo de sucesión regular

Sea  la sucesión S={4, 7, 10, 13, 16, ……}

Esta sucesión, denotada por S, es un conjunto numérico infinito, en este caso de números enteros.

Se puede apreciar que se trata de una sucesión regular, porque cada término se obtiene sumando 3 al término o elemento anterior:

4

4 +3 = 7

7+3 = 10

10+3 = 13

13+3 = 16

Dicho de otra manera: esta sucesión es regular porque la diferencia entre el término siguiente y el anterior da un valor fijo. En el ejemplo dado este valor es el 3.

A las sucesiones regulares que se obtienen sumando una cantidad fija al término anterior, también se les denomina progresiones aritméticas. Y a la diferencia -constante- entre términos sucesivos se le denomina razón y se denota como R.

Ejemplo de sucesión no regular y cuadrática

Véase ahora la siguiente sucesión:

S={ 2, 6, 12, 20, 30, ….}

Cuando se calculan las diferencias sucesivas se obtienen los siguientes valores:

6-2 = 4

12-6 = 6

20-12 = 8

30-20 = 10

Sus diferencias no son constantes, por lo que se puede afirmar que es una sucesión NO regular.

Sin embargo, si consideramos el conjunto de las diferencias, se tiene otra sucesión, la cual se denotará como S_dif:

S_dif = {4, 6, 8, 10, ….}

Esta nueva sucesión sí es una sucesión regular, ya que cada término se obtiene sumando el valor fijo R=2 al anterior. Por eso podemos afirmar que S es sucesión cuadrática.

Regla general para construir una sucesión cuadrática

Hay una fórmula general para construir una sucesión cuadrática:

T_n = A∙n² + B∙n +C

En esta fórmula, T_n es el término de la posición n de la sucesión. A, B y C son valores fijos, mientras que n va variando de uno en uno, es decir 1, 2, 3, 4, …

En la sucesión S del ejemplo anterior A=1, B=1 y C=0. De allí se deduce que la fórmula que genera todos los términos es: T_n = n² + n

Es decir:

T₁ = 1² + 1 = 2

T₂ = 2² + 2 = 6

T₃ = 3² + 3 = 12

T₅ = 5² + 5 = 30

T_n = n² + n

Diferencia entre dos términos consecutivos de una sucesión cuadrática

T_n+1 – T_n = [A∙(n+1)² + B∙(n+1) + C] – [A∙n² + B∙n +C]

Desarrollando la expresión mediante producto notable queda:

T_n+1 – T_n = A∙n² + A∙2∙n + A + B∙n + B + C – A∙n² – B∙n – C

Al simplificarla se obtiene:

T_n+1 – T_n = 2∙A∙n + A + B

Esta es la fórmula que da la sucesión de las diferencias S_Dif que puede escribirse así:

Dif_n = A∙(2n+1)+B

Donde claramente el término siguiente es 2∙A veces el anterior. Es decir, la razón de la sucesión de las diferencias S_dif es:  R= 2∙A.

Ejercicios resueltos de sucesiones cuadráticas

Ejercicio 1

Sea la sucesión S={1, 3, 7, 13, 21, ……}. Determine si:

i) Es regular o no

ii) Es cuadrática o no

iii) Fuese cuadrática, la sucesión de las diferencias y su razón

Respuestas

i) Calculemos la diferencia el término siguiente y el anterior:

3-1= 2

7-3= 4

13-7= 6

21-13= 8

Podemos afirmar que la sucesión S no es regular, porque la diferencia entre términos sucesivos no es constante.

ii) La sucesión de las diferencias sí es regular, porque la diferencia entre sus términos es el valor constante 2. Por lo tanto la sucesión original S es cuadrática.

iii) Ya determinamos que S es cuadrática, la sucesión de las diferencias es:

S_dif ={2, 4, 6, 8, …} y su razón es R=2.

Ejercicio 2

Sea la sucesión S={1, 3, 7, 13, 21, ……} del ejemplo anterior, donde se verificó que es cuadrática. Determine:

i) La fórmula que determina el término general T_{n .}

ii) Verifique el tercero y quinto término.

iii) El valor del décimo término.

Respuestas

i) La fórmula general de T_n es  A∙n² + B∙n +C. Entonces queda conocer los valores de A, B y C.

La sucesión de las diferencias tiene razón 2. Además para cualquier sucesión cuadrática la razón R es 2∙A según se demostró en los apartados anteriores.

R= 2∙A=2  lo que nos lleva a concluir que A=1.

El primer término de la sucesión de diferencias S_Dif es 2 y debe cumplir A∙(2n+1)+B, con n=1 y A=1, es decir:

2=1∙(2∙1+1)+B

despejando B se obtiene: B = -1

Luego el primer término de S (n=1) vale 1, es decir: 1 = A∙1² + B∙1 + C. Como ya sabemos que A=1 y B=-1, sustituyendo nos queda:

1=1∙1² + (-1)∙1 +C

Despejando C se obtiene su valor:  C = 1.

En resumen:

A=1, B=-1 y C=1

Entonces el término n-esimo será T_n = n² – n + 1

ii) El tercer término T₃ = 3² – 3 + 1 = 7 y se verifica. El quinto T₅ = 5² – 5 + 1 = 21 que también se verifica.

iii)  El décimo término será T₁₀ = 10² – 10 + 1 = 91.

Ejercicio 3

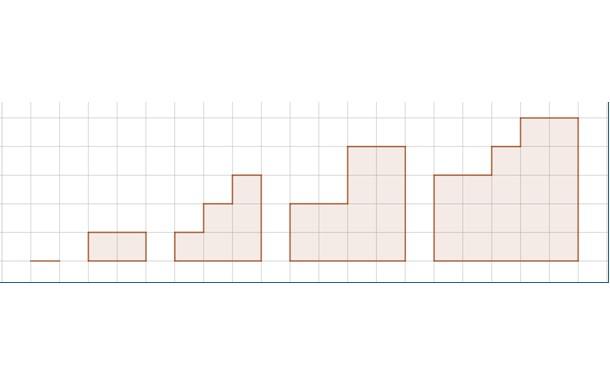
La figura muestra una secuencia de cinco figuras. El reticulado representa la unidad de longitud.

i) Determine la sucesión para el área de las figuras.

ii) Demuestre que se trata de una sucesión cuadrática.

iii) Encuentre el área de la figura # 10 (no mostrada).

Respuestas

i) La sucesión S correspondiente al área de la secuencia de figuras es:

S={0, 2, 6, 12, 20, . . . . . }

ii) La sucesión correspondiente a las diferencias consecutivas de los términos de S es:

S_dif = {2, 4, 6, 8, . . . . . }

Como la diferencias entre términos consecutivos no es constante, entonces S no es una sucesión regular. Falta saber si es cuadrática, para lo cual nuevamente hacemos la secuencia de las diferencias, obteniendo:

{2, 2, 2, …….}

Ya que todos los términos de la secuencia se repiten, se confirma que S es una sucesión cuadrática.

iii) La sucesión S_dif es regular y su razón R es 2. Utilizando la ecuación demostrada anteriormente R = 2∙A, queda:

2 = 2∙A, lo que implica que  A = 1.

El segundo término de la sucesión de diferencias S_Dif es 4 y el término n-ésimo de S_Dif es

A∙(2n+1)+B.

El segundo término tiene n=2. Además ya se determinó que A=1, así que usando  la ecuación anterior y sustituyendo se tiene:

4=1∙(2∙2+1)+B

Despejando B se obtiene: B = -1.

Se sabe que el segundo término de S vale 2, y que debe cumplir la fórmula del término general con n=2:

T_n = A∙n² + B∙n +C ;  n=2  ;  A=1  ;  B=-1    ;  T₂ = 2

Es decir

2 = 1∙2² – 1∙2 + C

Se concluye que C=0, es decir que la fórmula que da el término general de la sucesión S es:

T_n = 1∙n² – 1∙n +0 = n² – n

Ahora se verifica el quinto término:

T₅ = 5² – 5  = 20

iii) La figura #10, que no se ha dibujado aquí, tendrá el área correspondiente al décimo término de la sucesión S:

T₁₀ = 10² – 10  = 90

Referencias

1. https://www.geogebra.org