Inverso multiplicativo: explicación, ejemplos, ejercicios resueltos
Se entiende por inverso multiplicativo de un número, otro número que multiplicado por el primero da como resultado el elemento neutro del producto, es decir la unidad. Si se tiene un número real a entonces su inverso multiplicativo se denota por a-1, y se cumple que:
a a-1 = a-1 a = 1
Por lo general, el número a pertenece a conjunto de los números reales.
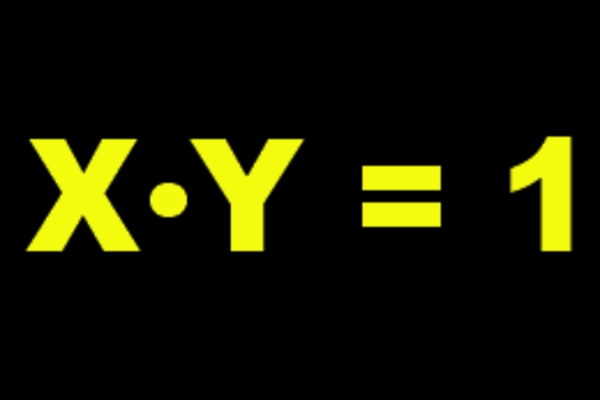
Si por ejemplo tomamos a = 2, entonces su inverso multiplicativo es 2-1 = ½ ya que se verifica lo siguiente:
2 ⋅ 2-1 = 2-1⋅ 2 = 1
2⋅ ½ = ½ ⋅ 2 = 1
Al inverso multiplicativo de un número también se le llama el recíproco, debido a que el inverso multiplicativo se obtiene intercambiando numerador y denominador, por ejemplo el inverso multiplicativo de 3/4 es 4/3.
Como regla general puede decirse que para un número racional (p/q) su inverso multiplicativo (p/q)-1 es recíproco (q/p) como puede verificarse a continuación:
(p/q) ⋅ (p/q)-1 = (p/q)⋅ (q/p) = (p⋅ q)/ (q⋅ p) = (p⋅ q)/(p⋅ q) = 1
El inverso multiplicativo no existe en el conjunto numérico de los enteros, por ejemplo si se toma el número entero 2 su inverso multiplicativo de acuerdo a lo visto anteriormente sería ½, pero un ½ no es un número entero.
Tampoco existe el inverso multiplicativo del elemento nulo de la multiplicación. En otras palabras, el número cero (0), que es el elemento nulo de la operación de multiplicación, no tiene inverso multiplicativo, ya que no existe ningún número que multiplicado por cero de la unidad.
El inverso multiplicativo existe en los números racionales, en los números reales y en los números complejos.
Ejemplos de inverso multiplicativo
Ejemplo 1
Hallar el inverso multiplicativo de 3/2 y verificar que cumple la propiedad de los enteros multiplicativos.
De acuerdo a la regla dada más arriba, se intercambia numerador y denominador de este modo el inverso multiplicativo de (3/2) es (2/3). Para verificar se realiza la multiplicación de los dos números:
(3/2) ⋅ (2/3) = (3 ⋅ 2) / (2 ⋅ 3) = 6/6 = 1.
Para multiplicar dos números fraccionarios simplemente se multiplica el numerador del primero por el numerador del segundo para obtener el numerador del resultado.
Para obtener el denominador de un producto de números fraccionarios se procede de forma similar, es decir se multiplican los denominadores entre sí y el resultado es el denominador del producto. En nuestro ejemplo se verifica que el numerador del producto del número y de su recíproco es 6 y el denominador es 6, quedando la fracción 6/6 que es 1.
Ejemplo 2
El inverso multiplicativo de -5 no debe confundirse con su simétrico (+5) que a veces se denomina inverso aritmético. El inverso multiplicativo se obtendrá de la siguiente manera:
(-5) ⋅ X = 1
Donde X es el inverso multiplicativo a ser obtenido. Un procedimiento posible consiste en despejar la incógnita X. Como (-5) multiplica a la incógnita X en el miembro izquierdo, entonces pasa dividiendo al miembro derecho:
X = 1 / (-5)
Como se sabe que + entre – es -, entonces finalmente se obtiene X:
X = – ⅕ .
En conclusión – ⅕ es el inverso multiplicativo de -5.
Ejemplo 3
Obtener el inverso multiplicativo de -√2. Supongamos que el inverso multiplicativo es X, entonces -√2 multiplicado por X debe ser la unidad, condición que imponemos a continuación:
-√2 ⋅ X = 1
A continuación se dividen ambos miembros por -√2 para obtener:
(-√2 ⋅ X) / (-√2) = 1 / (-√2)
En el primer miembro se simplifica -√2 quedando:
X = 1 / (-√2)
Esta expresión puede racionalizarse, es decir eliminar la raíz del denominador, multiplicando en el numerador por (-√2) y en el denominador por la misma cantidad para que no se altere el resultado:
X = (-√2) / [(-√2)(-√2)] = – (√2/2)
En conclusión – (√2/2) es el inverso multiplicativo de (-√2).
Ejemplo 4
Suponga un número cualquiera x, obtenga su inverso multiplicativo y represéntelo gráficamente.
En este caso se trata de una función f(x) = x, obtener el inverso multiplicativo es hallar la función g(x) tal que multiplicada por la primera nos de la unidad. La función g es la función recíproca de f y no debe confundirse de ninguna manera con su función inversa.
Dicho de otra manera el inverso multiplicativo de x es un y tal que se cumpla lo siguiente:
x ⋅ y = 1
de donde despejando y se tiene:
y = 1/x.
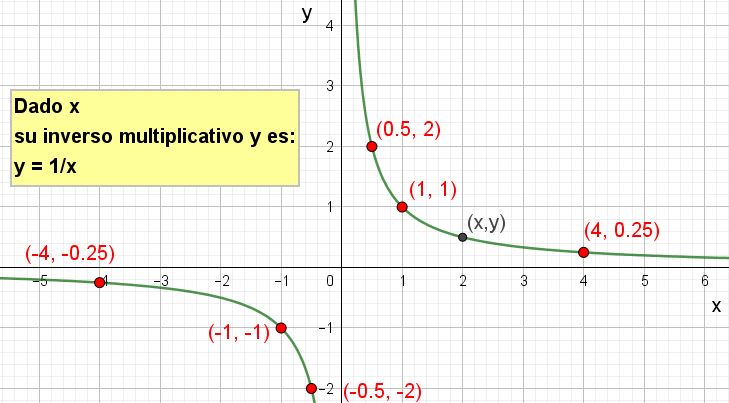
Lo anterior se interpreta así dado un valor de x, la fórmula anterior nos da su inverso multiplicativo.
Es posible hacer su representación gráfica como se muestra en la figura siguiente:
Ejercicios
Ejercicio 1
Dado x = 2 – √2, obtenga su inverso multiplicativo y.
Solución:
Para que y sea inverso multiplicativo de x debe cumplirse la siguiente igualdad:
x ⋅ y = 1
Se sustituye x por su valor:
(2 – √2) ⋅ y = 1
A continuación se despeja y:
y = 1 / (2 – √2)
Para racionalizar el resultado se multiplica numerador y denominador por su binomio conjugado:
y = (2 + √2) / ((2 + √2)(2 – √2))
En el denominador se reconoce un producto notable llamado el producto de una suma por una diferencia, el cual es la diferencia de los cuadrados. De esta manera desaparece la raíz en el denominador.
y = (2 + √2) / (2^2 – (√2)^2)
Resolviendo las potencias:
y = (2 + √2) / (4 – 2)
Simplificando:
y = (2 + √2) / 2
Ejercicio 2
Obtener el inverso multiplicativo de (1/a + 1/b) donde a y b son números reales diferentes de cero.
Solución:
Llamamos Y al inverso multiplicativo de (1/a + 1/b), de modo que debe cumplirse la siguiente ecuación:
Y ⋅ (1/a + 1/b) = 1
Se despeja la variable Y:
Y = 1 / (1/a + 1/b)
Se resuelve el denominador:
Y = 1 /( (b + a) / a b)
Como se sabe de las reglas del álgebra el denominador del denominador pasa al numerador:
Y = (a b) / (b + a)
Se ordena para finalmente obtener:
(a b) / (a + b) que es el inverso multiplicativo de (1/a + 1/b).
Ejercicio 3
Obtener el inverso multiplicativo de ( a – b) / ( a^2 – b^2 ).
Solución:
Recordemos que el inverso multiplicativo se denomina también el recíproco porque se obtiene justamente intercambiando numerador y denominador.
Entonces el inverso multiplicativo de ( a – b) / ( a^2 – b^2 ) será:
( a^2 – b^2 ) / ( a – b)
Pero esta expresión puede simplificarse si reconocemos, de acuerdo a las reglas del álgebra, que el numerador es una diferencia de cuadrados que puede factorizarse como el producto de una suma por una diferencia:
(( a + b )( a – b )) / ( a – b)
Como hay un factor común ( a – b ) en el numerador y en el denominador se procede a simplificar, obteniendo finalmente:
(a + b) que es el inverso multiplicativo de ( a – b) / ( a^2 – b^2 ).
Referencias
- Fuentes, A. (2016). MATEMÁTICAS BÁSICAS. Una Introducción al Cálculo. Lulu.com.
- Garo, M. (2014). Mathematics: quadratic equations: How solve a quadratic equation. Marilù Garo.
- Haeussler, E. F., & Paul, R. S. (2003). Matemáticas para administración y economía. Pearson Educación.
- Jiménez, J., Rofríguez, M., & Estrada, R. (2005). Matematicas 1 SEP. Umbral.
- Preciado, C. T. (2005). Curso de Matemáticas 3o. Editorial Progreso.
- Rock, N. M. (2006). Algebra I Is Easy! So Easy. Team Rock Press.
- Sullivan, J. (2006). Álgebra y Trigonometría. Pearson Educación.
