Prueba de hipótesis: qué es, ejemplo y ejercicio resuelto

¿Qué es la prueba de hipótesis?

La prueba de hipótesis, en estadística, es un procedimiento usado para comprobar cuán acertada es una conjetura acerca de una población. Dichas conjeturas se llaman hipótesis, que en principio se toman como verdaderas, hasta que alguna evidencia lo confirme o desmienta.

Esta evidencia es suministrada por los datos muestrales, aquellos que provienen de una porción significativa de la población, llamada muestra. La teoría de probabilidades suministra las técnicas necesarias para contrastar la veracidad de las hipótesis.

Ejemplos de hipótesis son:

-La temperatura promedio del cuerpo humano es 36.1 ºC.

-En promedio, una bolsa de maní salado producida en una fábrica de snacks pesa 50 g.

-Un 80% de los habitantes de una localidad, realizaron compras por Internet durante los últimos 6 meses.

-Las puntuaciones de test IQ para los estudiantes universitarios de una conocida institución, tiene una desviación estándar de 15.

-Una determinada variable aleatoria X sigue una distribución de Poisson.

Las cuatro primeras son del tipo de hipótesis paramétrica, pues se trata de afirmaciones acerca de algún parámetro de la población, como la media, la desviación estándar o alguna proporción.

En cambio, la última hipótesis establece la distribución de una variable aleatoria, y puesto que no hace referencia a algún parámetro o propiedad de la población, se dice que es una hipótesis no paramétrica.

Hipótesis nula e hipótesis alternativa

Hay dos clases de hipótesis con las cuales realizar una prueba, la cual servirá para contrastarlas:

-Hipótesis nula, denotada como H₀, establece que el parámetro bajo estudio tiene un valor establecido, o bien que la variable aleatoria sigue una determinada distribución. Por lo tanto, al expresar simbólicamente la hipótesis nula, siempre se utiliza el símbolo de la igualdad.

-Hipótesis alternativa: llamada H₁, afirma que el parámetro o la distribución son distintos a lo que asegura la hipótesis nula, de allí que, para expresar simbólicamente la hipótesis alternativa, se utilizan los símbolos: , > o ≠, pero nunca la igualdad.

Cuando se acepta la hipótesis nula, se rechaza la hipótesis alternativa, de manera que ambas son mutuamente excluyentes.

Nivel de significancia

Es una medida para el error que se puede cometer al realizar una prueba de hipótesis. Se define como la probabilidad de rechazar la hipótesis nula, siendo que es verdadera. Se denota usualmente con la letra griega α:

α = P (rechazar H₀ cuando es verdadera)

Los valores comúnmente usados para α son 0.01, 0.05, y 0.10; siendo el segundo el de uso más frecuente. Equivalen respectivamente a 1%, 5 % y 10% de probabilidad de equivocarse al rechazar H₀, pero en todo caso, cuanto menor sea el nivel de significancia, más confiable el resultado de la prueba.

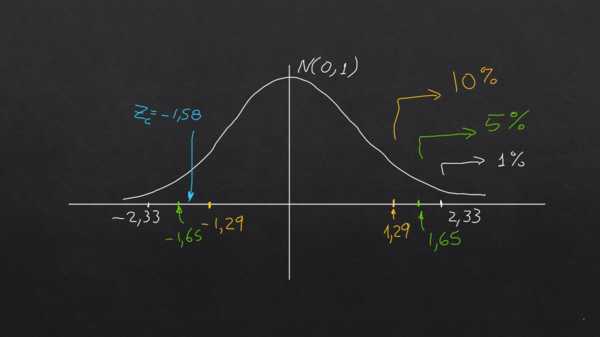
El valor alfa (α), puede entenderse como la fracción porcentual de área de la cola derecha (o izquierda), en una distribución normal tipificada (μ=0 y σ =1) y estos valores ocurren siempre en z= 2,33 para α= 0.01; en z= 1,65 para α= 1,65 y en z= 1,29 para α= 0,1.

Pasos para realizar una prueba de hipótesis

Paso 1

Definir respectivamente las hipótesis nula y alternativa. La hipótesis nula establece que el parámetro bajo estudio, llamado θ, es igual a un valor de referencia, denotado como θ₀:

H₀: θ = θ₀

Por ejemplo, si se investigan los efectos de un fármaco sobre cierta característica de una población de ratones de laboratorio, la hipótesis nula contempla que dicho fármaco no hace diferencia alguna en tal característica y que esta tiene un valor constante θ₀.

Para simbolizar la hipótesis nula siempre se emplea el signo de igualdad, en cambio, la hipótesis alternativa hace uso de alguno de los símbolos , > o ≠.

En el ejemplo del fármaco, la hipótesis alternativa establece que el compuesto sí tiene algún efecto sobre la característica en cuestión. Por lo tanto, esta es mayor, menor, o simplemente diferente del valor de referencia θ₀.

Paso 2

Escoger el nivel de significancia adecuado, que por lo general se establece en 5 %, tal como se indicó previamente.

Paso 3

Determinar la población y extraer de ella la muestra, o muestras, cuyo análisis servirá para contrastar las hipótesis y determinar la aceptación o el rechazo de la hipótesis nula.

Paso 4

Elegir y calcular el valor del estadístico de prueba para los datos recolectados, del cual se obtiene la evidencia necesaria para tomar la decisión de aceptar o rechazar la hipótesis nula. La elección del estadístico de prueba depende del parámetro seleccionado: media, desviación, proporción u otro.

El estadístico de prueba se obtiene al convertir un parámetro muestral en una puntuación z, un estadístico t de Student, r de Pearson o chi cuadrado, según el diseño experimental seleccionado. Existen fórmulas para ello.

Usualmente, si el parámetro poblacional es la media μ, “x barra” es la media muestral, se conoce la desviación estándar σ y el tamaño de muestra es n > 30, el estadístico de prueba z_C se calcula con la puntuación z:

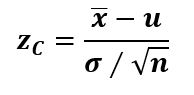
Y cuando n 30, pero σ es desconocida, se usa la t de Student.

Paso 5

Establecer criterios de aceptación o rechazo de la hipótesis nula, lo cual puede hacerse mediante dos procedimientos:

• A través de los valores de P.
• Por comparación con los valores críticos.

Los valores de P equivalen a la probabilidad de obtener los resultados encontrados, dado que la hipótesis nula es verdadera. Si estos valores son pequeños, se rechaza la hipótesis nula, si no lo son, se acepta. En todo caso, los valores de P no constituyen la prueba de que la hipótesis alternativa sea verdadera.

Se debe tener en cuenta que en una prueba de hipótesis es posible cometer dos tipos de error:

• Error tipo I: rechazar H₀ cuando es verdadera. Su probabilidad es α y equivale al nivel de significancia de la prueba.
• Error tipo II: aceptar H₀ cuando en realidad es falsa. Su probabilidad se denota como β.

Paso 6

Tomar la decisión de aceptar o rechazar la hipótesis nula. Si se usan los valores de P, cuando P α, se rechaza H₀ y se acepta H₁, y en caso contrario, se acepta H₀. El conjunto de valores P α se conoce como región crítica. Si el estadístico está en este intervalo se rechaza H₀.

Análogamente, se selecciona un valor crítico, según el parámetro poblacional elegido. Si este es la media, se procede como sigue:

• Prueba de una cola: θ θ₀ o θ > θ₀
• Prueba de dos colas: |θ| θ₀

Ejemplo resuelto

Una máquina fabrica tornillos cuyo valor nominal debe ser de 800 milímetros de largo, con una desviación estándar de 5%.

Se toma una muestra aleatoria, es decir en distintos días de la semana de producción, que totaliza unos 40 tornillos. Cuando se calcula la longitud promedio de la muestra, se obtiene el valor 790 milímetros.

Determinar si el largo promedio está en la tolerancia con niveles de significancia respectivamente de 1%, 5% y 10%.

Solución

Lo primero es calcular el estadístico de prueba del promedio, el cual en este caso es la desviación del promedio dividida entre el error estándar poblacional:

Zc= (790 – 800) / (40/√40) = -1,58

Donde se ha tomado en cuenta que un 5% de desviación estándar corresponde a 40 de 800.

La hipótesis nula es que el promedio de la muestra está dentro de la tolerancia permitida al nivel de significancia requerido, siempre que |Zc| sea menor que el valor tipificado |Zt|, de lo contrario se rechaza la hipótesis nula.

Para significancias de 1% y 5% se cumple la hipótesis nula, ya que |Zc| 2,33 y |Zc| 1,65 respectivamente.

Sin embargo, para significancia de 10% ocurre que |Zc| > 1,29. Es decir, que a este nivel de significancia no se cumple la hipótesis nula.

El siguiente gráfico aclara la conclusión: