Trapecio isósceles: propiedades, relaciones y fórmulas, ejemplos

Un trapecioisósceles es un cuadrilátero en el cual dos de los lados son paralelos entre sí y además, los dos ángulos adyacentes a uno de esos lados paralelos tienen la misma medida.

En la figura 1 se tiene el cuadrilátero ABCD, en el que los lados AD y BC son paralelos. Adicionalmente, los ángulos ∠DAB y ∠ADC adyacentes al lado paralelo AD tienen la misma medida α. 

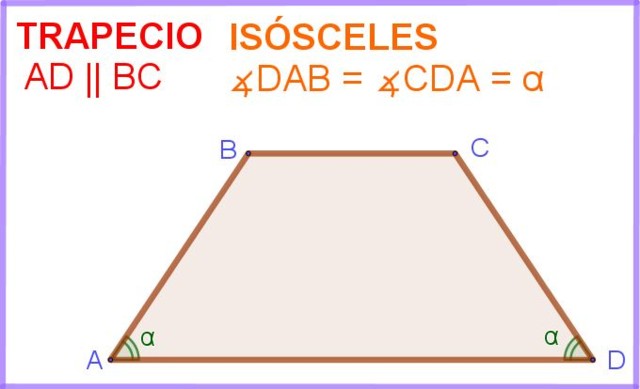
Así pues, este cuadrilátero, o polígono de cuatro lados es, en efecto, un trapecio isósceles.

En un trapecio, los lados paralelos se llaman bases y los no-paralelos se denominan laterales. Otra característica importante es la altura, que es la distancia que separa a los lados paralelos.

Además del trapecio isósceles hay otros tipos de trapecio:

-Trapecio escaleno, que tiene todos sus ángulos y lados diferentes.

-Trapecio rectángulo, en el que una lateral tiene ángulos adyacentes rectos.

La forma trapezoidal es frecuente en diversos ámbitos del diseño, la arquitectura, la electrónica, el cálculo y muchas más, como se verá más adelante. De allí la importancia de familiarizarse con sus propiedades.

Índice del artículo

• 1 Propiedades
  • 1.1 Exclusivas del trapecio isósceles
  • 1.2 Para todo trapecio
• 2 Relaciones y fórmulas
  • 2.1 Relaciones exclusivas del trapecio isósceles
  • 2.2 Relaciones para un trapecio cualquiera
  • 2.3 Relaciones para trapecio isósceles con circunferencia inscrita
  • 2.4 Fórmulas para determinar un lado, conocidos los otros y un ángulo
  • 2.5 Determinación de un lado, conocidos los otros y una diagonal
  • 2.6 Base a partir de la altura, el área y la otra base
  • 2.7 Lateral conocidas las bases, el área y un ángulo
  • 2.8 Lateral conocidas la mediana, el área y un ángulo
  • 2.9 Altura conocidos los lados
  • 2.10 Altura conocidos un ángulo y dos lados
  • 2.11 Diagonales conocidos todos los lados, o dos lados y un ángulo
  • 2.12 Perímetro del triángulo isósceles 
  • 2.13 Área del trapecio isósceles
  • 2.14 Radio de la circunferencia circunscrita
• 3 Ejemplos de uso del trapecio isósceles
  • 3.1 En arquitectura y construcción
  • 3.2 En diseño
• 4 Ejercicios resueltos
  • 4.1 – Ejercicio 1
  • 4.2 – Ejercicio 2
• 5 Referencias

Propiedades

Exclusivas del trapecio isósceles

Si un trapecio es isósceles entonces cumple las siguientes propiedades características:

1.- Las laterales tienen la misma medida.

2.- Los ángulos adyacentes a las bases son iguales.

3.- Los ángulos opuestos son suplementarios.

4.- Las diagonales tienen igual longitud, siendo las mismas los dos segmentos que unen los vértices opuestos.

5.- El ángulo formado entre las bases y las diagonales son todos de la misma medida.

6.- Tiene circunferencia circunscrita.

Recíprocamente, si un trapecio cumple alguna de las propiedades anteriores, entonces es un trapecio isósceles.

Si en un trapecio isósceles uno de los ángulos es recto (90º), entonces todos los otros ángulos también lo serán, formando un rectángulo. Es decir, un rectángulo es un caso particular de trapecio isósceles.

Para todo trapecio

El siguiente conjunto de propiedades son válidas para cualquier trapecio:

7.- La mediana del trapecio, es decir el segmento que une los puntos medios de sus lados no paralelos, es paralelo a cualquiera de las bases.

8.- La longitud de la mediana es igual a la semisuma (suma dividida entre 2) de la de sus bases.

9.- La mediana de un trapecio corta a sus diagonales en el punto medio.

10.- Las diagonales de un trapecio se intersectan en un punto que las dividen en dos secciones proporcionales a los cocientes de las bases.

11.- La suma de los cuadrados de las diagonales de un trapecio es igual a la suma de los cuadrados de sus laterales más el doble producto de sus bases.

12.- El segmento que une los puntos medios de las diagonales tiene longitud igual a la semidiferencia de las bases.

13.- Los ángulos adyacentes a las laterales son suplementarios.

14.- Un trapecio tiene circunferencia inscrita si y solo si la suma de sus bases es igual a la suma de sus laterales.

15.- Si un trapecio tiene circunferencia inscrita, entonces los ángulos con vértice en el centro de dicha circunferencia y lados que pasen por los extremos de una misma lateral, son ángulos rectos.

Relaciones y fórmulas

El siguiente conjunto de relaciones y fórmulas están referidas a la figura 3, donde además del trapecio isósceles se muestran otros segmentos importantes ya mencionados, como diagonales, altura y mediana.

Relaciones exclusivas del trapecio isósceles

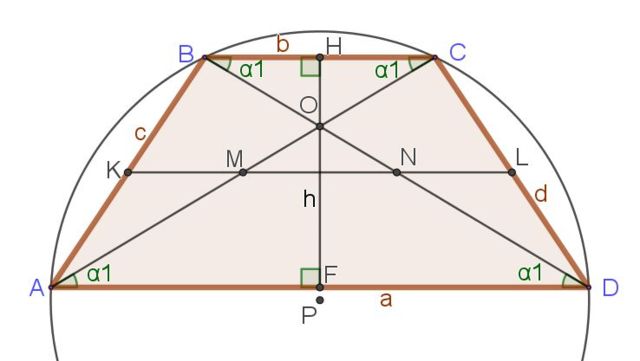
1.- AB = DC = c = d

2.- ∡DAB = ∡CDA y ∡ABC= ∡BCD

3.- ∡DAB + ∡BCD = 180º y ∡CDA + ∡ABC = 180º

4.- BD = AC

5.- ∡CAD = ∡BDA = ∡CBD = ∡BCA = α₁

6.- A, B, C y D pertenecen  a la circunferencia circunscrita.

Relaciones para un trapecio cualquiera

1. Si AK = KB y DL = LC ⇒ KL || AD y KL || BC

8.- KL = (AD + BC)/2

9.- AM = MC = AC/2 y DN = NB = DB/2

10.- AO/OC = AD/BC y DO/OB = AD/BC

11.- AC² + DB² = AB² + DC² + 2⋅AD⋅BC

12.- MN = (AD – BC)/2

13.- ∡DAB + ∡ABC = 180º y ∡CDA + ∡BCD = 180º

14.- Si AD + BC = AB + DC ⇒ ∃ R que equidista de AD, BC, AB y DC

15.- Si ∃ R que equidista de AD, BC, AB y DC, entonces:

∡BRA = ∡DRC = 90º

Relaciones para trapecio isósceles con circunferencia inscrita

Si en un trapecio isósceles la suma de las bases es igual al doble de una lateral, entonces existe la circunferencia inscrita.

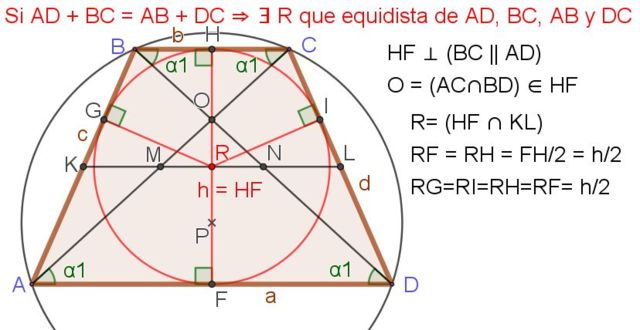
Las siguientes propiedades se aplican cuando el trapecio isósceles tiene circunferencia inscrita (ver figura 4 arriba):

16.- KL = AB = DC = (AD + BC)/2

17.- Las diagonales se cortan en ángulo recto: AC ⊥ BD

18.- La altura mide igual que la mediana: HF = KL, es decir h = m.

19.- El cuadrado de la altura es igual al producto de las bases: h² = BC⋅AD

20.- En estas condiciones específicas, el área del trapecio es igual al cuadrado de la altura o el producto de las bases: Área= h² = BC⋅AD.

Fórmulas para determinar un lado, conocidos los otros y un ángulo

Conocida una base, la lateral y un ángulo, la otra base puede determinarse mediante:

a = b + 2c Cos α

b = a – 2c Cos α

Si se da como dato conocido la longitud de las bases y un ángulo entonces las longitudes de ambas laterales es:

c = (a – b) / ( 2 Cos α)

Determinación de un lado, conocidos los otros y una diagonal

a = (d₁² – c²)/ b;

b = (d₁² – c²)/ a 

c = √( d₁² – a⋅b )

Donde d₁ es la longitud de las diagonales.

Base a partir de la altura, el área y la otra base

a = (2 A)/h – b

b = (2 A)/h – a

Lateral conocidas las bases, el área y un ángulo

c = (2A) /[(a + b) sen α]

Lateral conocidas la mediana, el área y un ángulo

c = A / (m.sen α)

Altura conocidos los lados

h = √[4 c² – (a – b)²]

Altura conocidos un ángulo y dos lados

h = tg α⋅(a – b)/2 = c . sen α

Diagonales conocidos todos los lados, o dos lados y un ángulo

d₁ = √(c²+ a b)

d₁ = √(a²+ c² – 2 a c Cos α)

d₁ = √(b² + c²– 2 b c Cos β)

Perímetro del triángulo isósceles 

P = a + b + 2c

Área del trapecio isósceles

Hay varias fórmulas para calcular el área, dependiendo de los datos que se conozcan. La siguiente es la más conocida, en función de las bases y la altura:

A = h⋅(a + b)/2

Y también se pueden usar estas otras:

-Si se conocen los lados

A = [(a +b)/4] √[4c² – (a – b)²]

-Cuando se tienen dos lados y un ángulo

A = (b + c Cos α) c Sen α = (a – c Cos α) c Sen α

-Si se conoce el radio de la circunferencia inscrita y un ángulo

A = 4 r² / Sen α = 4 r² / Sen β

-Cuando se conocen las bases y un ángulo

A = a⋅b / Sen α = a⋅b / Sen β 

-Si el trapecio se puede inscribir una circunferencia

A = c⋅√(a⋅b) = m⋅√(a⋅b) = r⋅(a + b)/2

-Conocida las diagonales y el ángulo que forman entre sí

A = (d₁²/2) Sen γ = ( d₁² / 2) Sen δ 

-Cuando se tiene la lateral, la mediana y un ángulo

A = mc.sen α = mc.sen β

Radio de la circunferencia circunscrita

Solo los trapecios isósceles tienen circunferencia circunscrita. Si se conoce la base mayor a, la lateral c  y la diagonal d₁, entonces el radio R de la circunferencia que pasa por los cuatro vértices del trapecio es:

R = a⋅c⋅d₁ / 4√[p (p -a) (p -c) (p – d₁)]

Donde p = (a + c + d₁) / 2

Ejemplos de uso del trapecio isósceles

El trapecio isósceles aparece en el campo del diseño, como se observa en la figura 2. Y aquí tenemos algunos ejemplos adicionales:

En arquitectura y construcción

Los antiguos incas conocían al trapecio isósceles y lo usaron como elemento de construcción en esta ventana de Cuzco, Perú:

Y aquí aparece de nuevo el trapecio en la llamada chapa trapezoidal, un material de uso frecuente en construcción:

En diseño

Ya vimos que el trapecio isósceles aparece en objetos cotidianos, inclusivo alimentos como esta barra de chocolate:

Ejercicios resueltos

– Ejercicio 1

Un trapecio isósceles tiene base mayor de 9 cm, base menor de 3 cm y sus diagonales 8 cm cada una. Calcular:

a) Laterales

b) Altura

c) Perímetro

d) Ärea

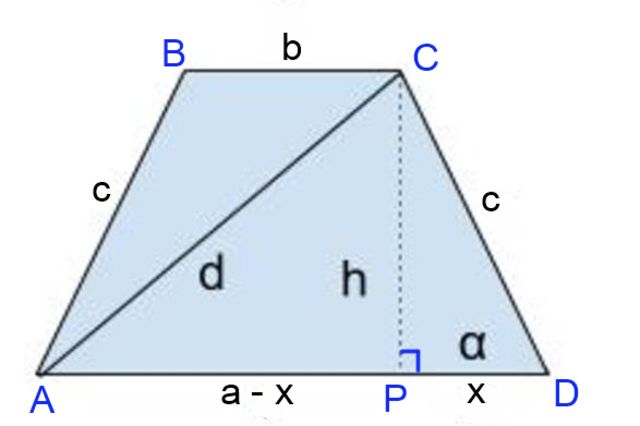
Solución a

Se traza la altura CP = h, donde el pie de la altura define los segmentos:

PD = x = (a-b)/2 y 

AP = a – x = a – a/2 + b/2 = (a+b)/2.

Mediante el teorema de Pitágoras al triángulo rectángulo DPC:

c² = h² + (a – b)² /4

Y también al triángulo rectángulo APC:

d² = h² + AP² = h² + (a+b)² /4

Por último se resta miembro a miembro, la segunda ecuación de la primera y se simplifica:

d² – c² = ¼ [(a+b)² – (a-b)²] = ¼ [(a+b+a-b)(a+b-a+b)]

d² – c² = ¼ [2a 2b] = a b

c²= d² – a b ⇒ c= √(d² – a b)= √(8² – 9⋅3)= √37= 6,08 cm

Solución b

h² = d² – (a+b)² /4= 8² – (12² / 2² )= 8² – 6² = 28

h = 2 √7 = 5,29 cm

Solución c

Perímetro= a + b + 2 c= 9 + 3 + 2⋅6,083= 24,166 cm

Solución d

Área= h (a+b)/2 = 5,29 (12)/2= 31,74 cm

– Ejercicio 2

Se tiene un trapecio isósceles cuya base mayor es el doble de la menor y su base menor es igual a la altura, la cual es 6 cm. Determinar:

a) La longitud de la lateral

b) Perímetro

c) Área

d) Ángulos

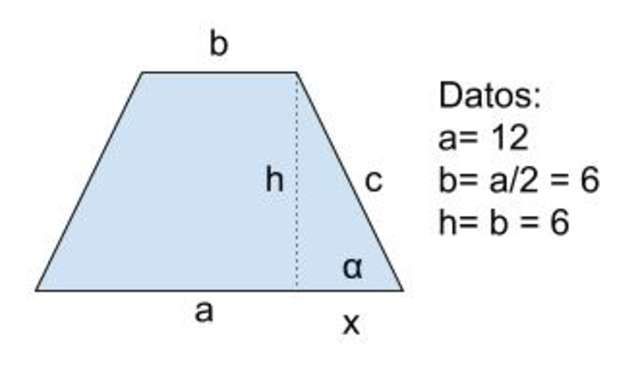
Solución a

Datos: a= 12, b= a/2 = 6 y h= b = 6

Se procede de esta forma: se traza la altura h y se aplica el teorema de Pitágoras al triángulo de hipotenusa “c” y catetos h y x:

c² = h²+xc²

Luego hay que calcular el valor de la altura a partir de los datos (h = b) y el del cateto x: 

a = b + 2 x ⇒ x= (a-b)/2

Sustituyendo las expresiones anteriores se tiene:

c² = b²+(a-b)²/2²

Ahora se introducen los valores numéricos y se simplifica:

c² = 62+(12-6)2/4

c² = 62(1+¼)= 62(5/4)

Obteniéndose:

c = 3√5 =6,71 cm

Solución b

El perímetro P = a + b + 2 c

P= 12 + 6 + 6√5 = 6(8+√5) = 61,42 cm

Solución c

El área en función de la altura y la longitud de las bases es:

A = h⋅(a + b)/2 = 6⋅(12 + 6)/2 = 54 cm²

Solución d

El ángulo α que forma la lateral con la base mayor se obtiene por trigonometría:

Tan(α) = h / x = 6/3 = 2

α = ArcTan(2) = 63,44º

El otro ángulo, el que forma la lateral con la base menor es β, que es suplementario de α:

β = 180º – α = 180º – 63,44º= 116,56º

Referencias

1. E. A. 2003. Elementos de geometría: con ejercicios y geometría del compás. Universidad De Medellín.
2. Campos, F. 2014. Matemáticas 2. Grupo Editorial Patria.
3. Freed, K. 2007. Discover Polygons. Benchmark Education Company.
4. Hendrik, V. 2013. Generalized Polygons. Birkhäuser.
5. IGER. Matemática Primer Semestre Tacaná. IGER.
6. Jr. geometry. 2014. Polygons. Lulu Press, Inc.
7. Miller, Heeren, & Hornsby. 2006. Matemática: Razonamiento Y Aplicaciones. 10ma.  Edición. Pearson Educación.
8. Patiño, M. 2006. Matemáticas 5. Editorial Progreso.
9. Wikipedia. Trapecio. Recuperado de: es.wikipedia.com