Ley de Ampère: fórmula y ecuaciones, demostración, ejercicios
La ley de Ampère establece que la circulación del vector inducción magnética B es proporcional a la intensidad I de la corriente que fluye por el mismo.
A su vez la circulación de B es la suma de todos los productos entre la componente tangencial B║ y la longitud de un pequeño segmento Δℓ de una curva cerrada C, alrededor de un circuito. En términos matemáticos se escribe así:
∑ B║ .Δℓ ∝ I
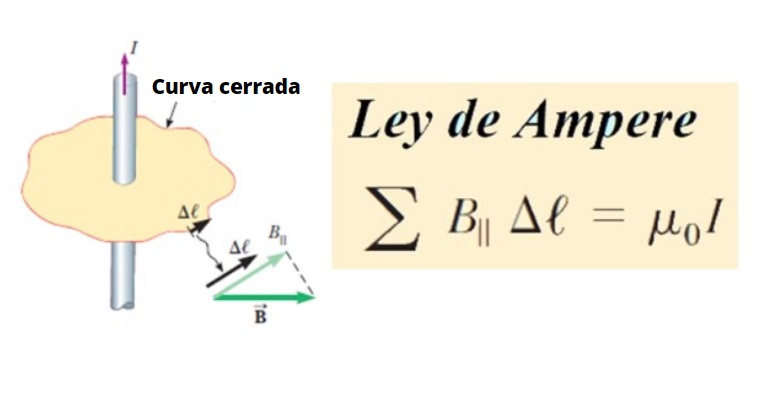
Como una línea o curva arbitraria C, se puede dividir en pequeños segmentos Δℓ, y estos a su vez pueden ser infinitesimales, pasan entonces a llamarse dℓ.
En tal caso, la sumatoria se convierte en una integral de línea del producto escalar entre los vectores B y ds. Dicho producto contiene la componente tangencial de B, que es B cosθ, donde θ es el ángulo entre los vectores:
El pequeño círculo que atraviesa la integral significa que la integración se lleva a cabo sobre una trayectoria cerrada C, la que en este caso envuelve la corriente que fluye a través de la sección transversal del conductor.
La constante de proporcionalidad necesaria para establecer la igualdad es μo, la permeabilidad del vacío. De esta forma, la ley de Ampère queda:
La ley de Ampère nos dice que la integral de línea ∫CB ∙ ds vale exactamente μoI, pero no nos ofrece los detalles acerca de cómo se orienta el campo magnético B respecto a la curva C en cada punto, ni sobre la forma de calcular la integral. Solamente nos dice que el resultado de la misma siempre es μoI.
Índice del artículo
La ley de Ampère se verifica experimentalmente comprobando el campo magnético producido por un conductor rectilíneo muy largo. Antes de abordar el problema, hay que resaltar dos casos de especial interés en la ecuación anterior:
-El primero es cuando B y ds son paralelos, lo que significa que B es tangencial a C. Entonces el ángulo entre ambos vectores es 0º y el producto escalar es simplemente el producto de las magnitudes B.ds.
-El segundo ocurre si B y ds son perpendiculares, en cuyo caso el producto escalar es 0, ya que el ángulo entre los vectores es 90º, cuyo coseno es 0.
Otro detalle importante es la elección de la curva C sobre la cual se evalúa la circulación del campo. La ley de Ampère no especifica cuál puede ser, pero sí debe envolver a la distribución de corriente. Tampoco dice en qué sentido recorrer la curva y hay dos posibilidades para esto.
La solución está en asignar signos según la regla del pulgar derecho. Los cuatro dedos se curvan en la dirección en la que se quiere integrar, usualmente esta será la misma en que el campo B circula. Si la corriente apunta en el sentido del pulgar derecho se le asigna signo + y si no, signo -.
Esto se aplica cuando hay una distribución con varias corrientes, algunas pueden ser positivas y otras negativas. La suma algebraica de ellas es la que vamos a colocar en la ley de Ampère, la cual se suele nombrar como corriente encerrada (por la curva C).
En la figura 2 se muestra un alambre que transporta una corriente I fuera del plano. La regla del pulgar derecho asegura que B circula en sentido contrario al reloj, describiendo circunferencias como lo muestran las flechas rojas.
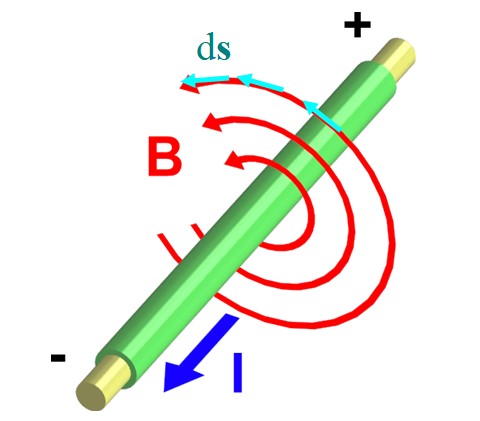
Tomemos una de ellas, cuyo radio es r. La dividimos en pequeños segmentos diferenciales ds, representados mediante los vectores en azul. Ambos vectores, B y ds, son paralelos en cada punto de la circunferencia, y de esta forma la integral ∫CB ∙ ds se transforma en:
∫C Bds
Ello se debe a que, como dijimos antes, el producto escalar B ∙ ds es el producto de las magnitudes de los vectores por el coseno de 0º. El resultado de la integral lo conocemos gracias a la ley de Ampère, por lo tanto escribimos:
∫C Bds = μoI
Puesto que la magnitud del campo es constante sobre toda la trayectoria, sale de la integral:
B ∫C ds = μoI
La integral ∫C ds representa la sumatoria de todos los segmentos infinitesimales que componen la circunferencia de radio r, equivalente a la longitud de la misma, el producto de su radio por 2π:
B.2πr = μoI
Y de allí encontramos que la magnitud de B es:
B = μoI / 2πr
Es preciso recalcar que aun si la trayectoria seleccionada (o circuito amperiano) no fuese circular, el resultado de la integral continúa siendo μoI, sin embargo ∫CB ∙ ds ya no sería B.2πr.
Por eso la utilidad de la ley de Ampère para determinar el campo magnético radica en escoger distribuciones con alta simetría, tales que la integral sea fácil de evaluar. Las trayectorias circulares y rectilíneas cumplen con este requisito.
Considere las curvas a, b, c y d mostradas en la figura 3. Ellas envuelven tres corrientes, dos que salen del plano, simbolizadas con un punto ( . ), cuyas intensidades son 1 A y 5 A, y una corriente que entra al plano, lo cual se denota con una cruz y cuya magnitud es 2 A.
Encuentre la corriente encerrada por cada curva.
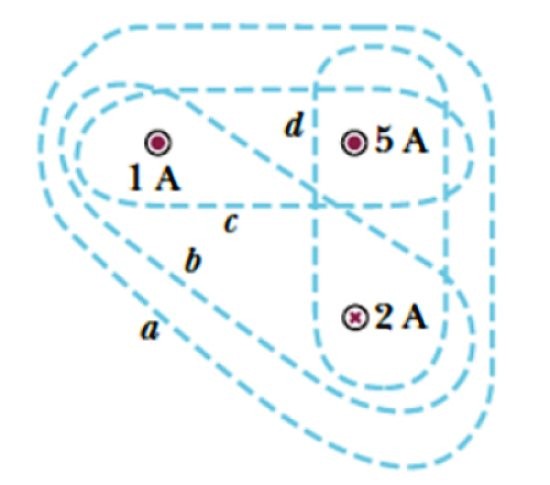
Solución
A las corrientes que salen del papel se les asigna signo +. De acuerdo a esto:
Curva a
Encierra las tres corrientes, por lo tanto la corriente encerrada es + 1 A + 5 A – 2 A = 4 A.
Curva b
Solamente las corrientes de 1 A y – 2 A están dentro de esta curva, por lo tanto la corriente encerrada es de – 2 A.
Curva c
Encierra las corrientes salientes 1A y 5 A, por lo tanto la corriente encerrada es 6 A.
Curva d
Las corrientes en su interior son +5 A y – 2 A, entonces encierra una corriente neta de 3 A.
Calcular la magnitud del campo magnético producido por un alambro rectilíneo muy largo, en un punto situado a 1 metros del mismo, si el alambre transporta una corriente de 1 A.
Solución
Según la ley de Ampère, el campo del alambre viene dado por:
B = μoI / 2πr = (4π x 10-7 x 1 / 2π x 1) T = 2 x 10-7 T.
- Figueroa, D. (2005). Serie: Física para Ciencias e Ingeniería. Volumen 6. Electromagnetismo. Editado por Douglas Figueroa (USB).
- Knight, R. 2017. Physics for Scientists and Engineering: a Strategy Approach. Pearson.
- Sears, Zemansky. 2016. University Physics with Modern Physics. 14th. Ed. Volume 2.
- Serway, R. 2009. College Physics. Cengage Learning.
- Tipler, P. (2006) Física para la Ciencia y la Tecnología. 5ta Ed. Volumen 2. Editorial Reverté.
