Mínimos cuadrados: qué es, método, ejercicios resueltos

¿Qué es el método de mínimos cuadrados?

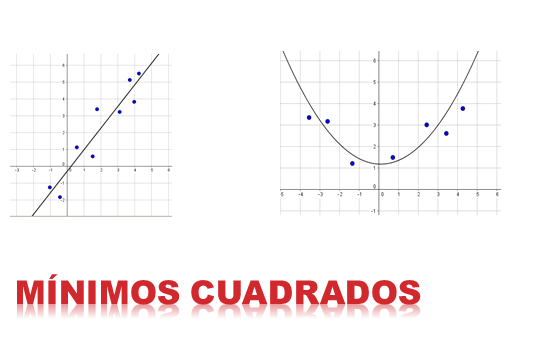
El método de mínimos cuadrados es una de las aplicaciones más importantes en la aproximación de funciones. La idea es encontrar una curva tal que, dado un conjunto de pares ordenados, dicha función se aproxime mejor a los datos. La función puede ser una recta, una curva cuadrática, una cúbica, etc.

La idea del método consiste en minimizar la suma de cuadrados de las diferencias en las ordenadas (componente Y), entre los puntos generados por la función elegida y los puntos pertenecientes al conjunto de datos.

Método de mínimos cuadrados

Antes de dar el método, primero debemos tener claro lo que significa “se aproxime mejor”. Supongamos que se busca una recta y=b+mx que sea la que mejor represente a un conjunto de n puntos, a saber {(x1,y1),(x2,y2)…,(xn,yn)}.

Como se muestra en la figura anterior, si las variables x y y estuvieran relacionadas por la recta y=b+mx, entonces para x=x1 el valor correspondiente de y sería b+mx1. Sin embargo, este valor es diferente del verdadero valor de y, que es y=y1.

Recordemos que en el plano, la distancia entre dos puntos viene dada por la siguiente fórmula:

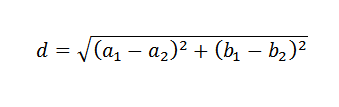
Con esto en mente, para determinar la manera de escoger la recta y=b+mx que mejor se aproxime a los datos dados, suena lógico usar como criterio la selección de la recta que minimice la suma de los cuadrados de las distancias entre los puntos y la recta.

Como la distancia entre los puntos (x1,y1) y (x1,b+mx1) es y1-(b+mx1), nuestro problema se reduce a encontrar números m y b tales que la siguiente suma sea mínima:

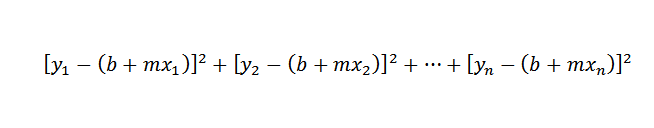
La recta que cumple con esta condición se conoce como la “aproximación de la recta de mínimos cuadrados a los puntos (x1,y1),(x2,y2),…,(xn,yn)”.

Una vez obtenido el problema, solo queda escoger un método para encontrar la aproximación por  mínimos cuadrados. Si los puntos (x1,y1),(x2,y2),…,(xn,yn) están todos en la recta y=mx+b, tendríamos que son colineales y:

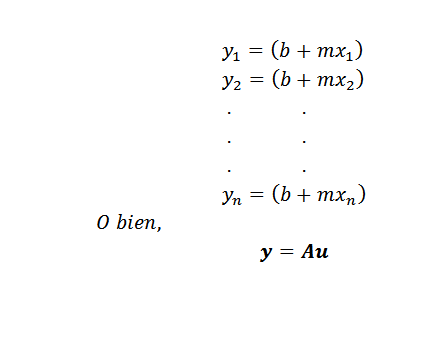
En esta expresión:

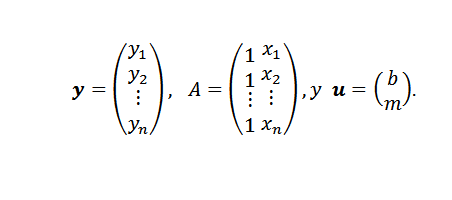
Finalmente, si los puntos no son colineales, entonces y-Au=0 y el problema se puede traducir en encontrar un vector u tal que la norma euclidiana sea mínima.

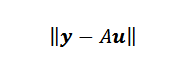
Encontrar el vector minimizante u no es tan difícil como se podría llegar a pensar. Como A es una matriz nx2 y u es una matriz 2×1, tenemos que  el vector Au es un vector en Rⁿ y pertenece a la imagen de A, la cual es un subespacio de Rⁿ con una dimensión no mayor que dos.

Supondremos que n=3 para mostrar cuál es el procedimiento que se debe seguir. Si n=3, la imagen de A será un plano o una recta que pasa por el origen.

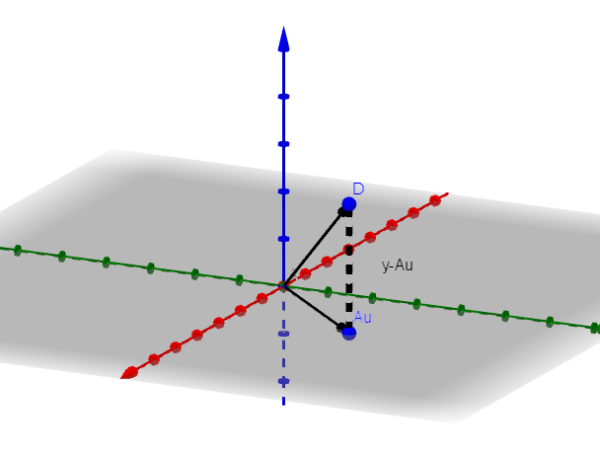
Sea v el vector minimizante. En la figura observamos que y-Au se minimiza cuando es ortogonal a la imagen de A. Es decir, si v es el vector minimizante, entonces ocurre que:

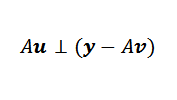
Luego, podemos expresar lo anterior de esta forma:

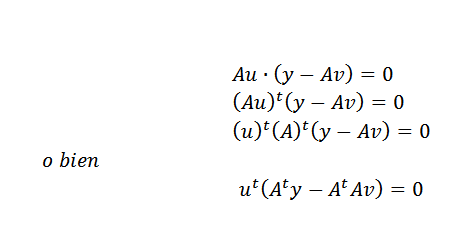
Esto solo puede ocurrir si:

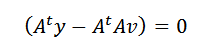
Finalmente, despejando v, tenemos que:

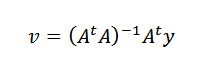
Es posible hacer esto ya que A^tA es invertible siempre que los n puntos dados como datos no sean colineales.

Ahora, si en vez de buscar una recta deseáramos hallar una parábola (cuya expresión sería  de la forma y=a+bx+cx²) que fuera una mejor aproximación a los n puntos datos, el procedimiento sería el descrito a continuación.

Si los n puntos datos estuvieran en dicha parábola, se tendría que:

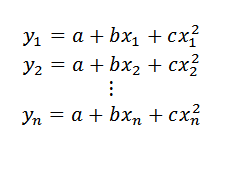
Luego:

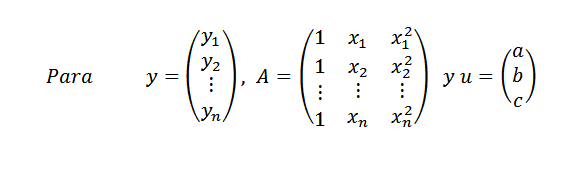
De manera similar podemos escribir y=Au. Si todos los puntos no están en la parábola, tenemos que y-Au es distinto de cero para cualquier vector u y nuestro problema vuelve a ser: encontrar un vector u en R3 tal que su norma ||y-Au|| sea lo menor posible.

Repitiendo el procedimiento anterior, podemos llegar a que el vector buscado es:

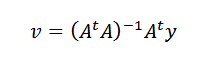
Ejercicios resueltos

Ejercicio 1

Encontrar la recta que mejor se ajuste a los puntos (1,4), (-2,5), (3,-1) y (4,1).

Solución

Tenemos que:

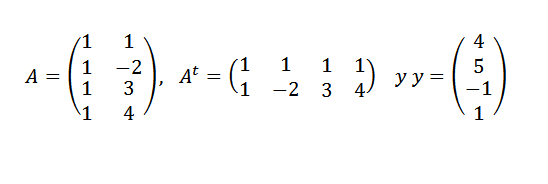
Luego:

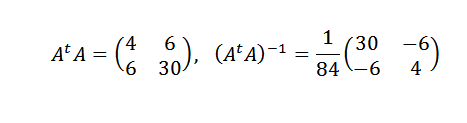
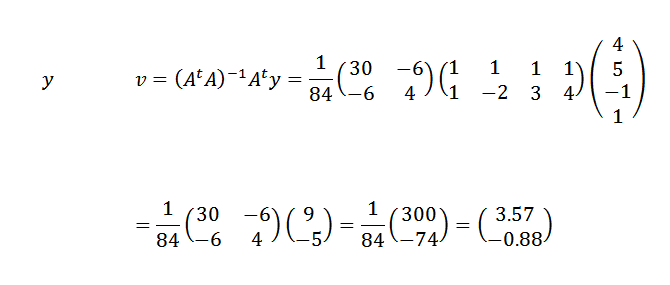
Por lo tanto, concluimos que la recta que mejor se ajusta a los puntos está dada por:

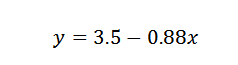
Ejercicio 2

Supongamos que se deja caer un objeto desde una altura de 200 m. Mientras cae, se toman las siguientes medidas:

Sabemos que la altura de dicho objeto, después de haber transcurrido un tiempo t, viene dada por:

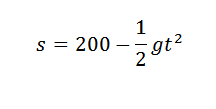
Si deseáramos obtener el valor de g, podemos buscar una parábola que sea una mejor aproximación a los cinco puntos dados en la tabla, y así tendríamos que el coeficiente que acompaña a t² será una aproximación razonable a (-1/2)g si las mediciones son exactas.

Tenemos que:

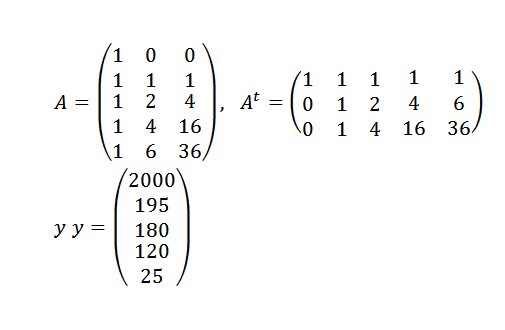
Y luego:

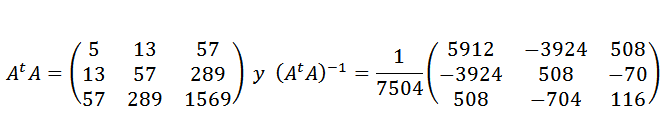
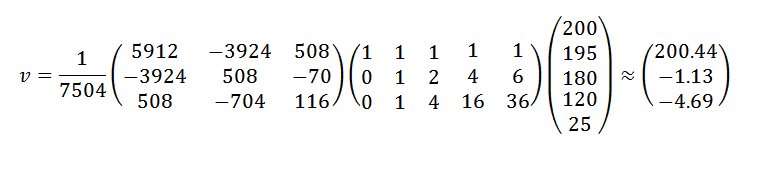
Así que los puntos de datos se ajustan por la siguiente expresión cuadrática:

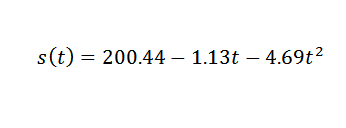
Entonces, se tiene que:

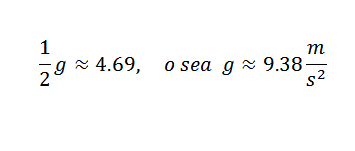
Este es un valor que está razonablemente cerca del correcto, que es g=9,81 m/s². Para poder obtener una aproximación más exacta de g sería necesario partir de observaciones más precisas.

¿Para qué sirve el método de mínimos cuadrados?

En los problemas que se dan en las ciencias naturales o sociales es conveniente escribir las relaciones que se dan entre diferentes variables por medio de alguna expresión matemática.

Por ejemplo, podemos relacionar en economía el costo (C), los ingresos (I) y las utilidades (U) por medio de una sencilla fórmula:

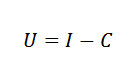
En física, podemos relacionar la aceleración causada por la gravedad, el tiempo en que un objeto ha estado cayendo y la altura del objeto por la ley:

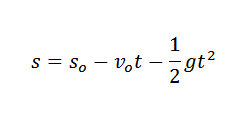
En la expresión anterior s_o es la altura inicial de dicho objeto y v_o es su velocidad inicial.

Sin embargo, encontrar fórmulas como estas no es una tarea sencilla; por lo general le corresponde al profesional de turno trabajar con muchos datos y realizar repetidamente varios experimentos (a fin de verificar que los resultados obtenidos son constantes) para encontrar relaciones entre los diferentes datos.

Una manera común de lograr esto es representar los datos obtenidos en un plano como puntos y buscar una función continua que se aproxime de manera óptima a dichos puntos.

Una de las maneras de encontrar la función que “mejor se aproxime” a los datos dados es por el método de los mínimos cuadrados.

Además, como vimos también en el ejercicio, gracias a este método podemos conseguir aproximaciones bastantes cercanas a constantes físicas.