Fórmula general: ecuaciones cuadráticas, ejemplos, ejercicios

La fórmula general, que también se conoce como la fórmula resolvente en algunos textos, se utiliza para resolver ecuaciones de segundo grado: ax² + bx + c = 0.

En ellas a, b y c son números reales, con la condición de que a sea diferente de 0, siendo x la incógnita. Entonces, la fórmula general presenta el despeje de la incógnita mediante una expresión que involucra los valores de a, b y c de la siguiente manera:

Y mediante esta fórmula se puede encontrar la solución de cualquier ecuación de segundo grado o cuadrática, siempre que dicha solución exista.

Según los historiadores, la fórmula general era conocida ya por los antiguos matemáticos babilonios. Posteriormente fue transmitida a otros pueblos, como los egipcios y los griegos, mediante intercambios culturales.

La fórmula y sus variantes llegaron a Europa gracias a los matemáticos musulmanes asentados en la península ibérica. Sin embargo, ellos no utilizaban la notación algebraica que empleamos en la actualidad. Esta notación se debe al matemático francés y experto criptógrafo del siglo XVI Francois Viete.

Índice del artículo

• 1 Ecuaciones cuadráticas por la fórmula general
  • 1.1 Demostración de la fórmula general
• 2 Ejemplos de uso de la fórmula general
  • 2.1 – Ejemplo 1
  • 2.2 – Ejemplo 2
• 3 Ejercicio resuelto
  • 3.1 Solución
• 4 Referencias

Ecuaciones cuadráticas por la fórmula general

Vamos a ver cómo surge la fórmula general, para así comprobar su validez. Partiendo de una ecuación cuadrática general:

ax² + bx + c = 0

Pongamos en práctica algunas manipulaciones algebraicas simples, para lograr el despeje de la incógnita. Hay varias formas de llevar esto a cabo, por ejemplo completando cuadrados, como se muestra seguidamente.

Demostración de la fórmula general

Comenzamos por sumar (–c) a ambos lados de la igualdad:

ax² + bx = – c

Y ahora se multiplica por 4a, siempre a ambos lados de la igualdad, para no alterar la expresión:

4a² x² + 4ab x = – 4ac

Sumando b²:

4a²⋅x² + 4ab⋅x + b² = – 4ac + b²

La finalidad de esto es completar cuadrados en el lado izquierdo de la igualdad, el que contiene la incógnita, de esta manera se facilita su despeje. De esta forma:

-El primer término: 4a² x² es el cuadrado perfecto de 2ax

-El último, que es b², es el cuadrado perfecto de b.

-Y el término central es el doble producto de 2ax y b: 2⋅2ax⋅b = 4abx

Por lo tanto tenemos un binomio al cuadrado:

4a²⋅x² + 4ab⋅x + b² = (2ax + b)²

Y podemos escribir:

(2ax + b)² = – 4ac + b²

Estamos a un paso de despejar la incógnita x:

Y ya obtenemos la fórmula general que conocemos:

Hay otras formas de manipular algebraicamente la ecuación cuadrática y obtener este mismo resultado.

Ejemplos de uso de la fórmula general

Para aplicar la fórmula general se determinan cuidadosamente los valores de a, b y c y se sustituyen en la fórmula. Nótese el símbolo más/menos en el numerador; esto indica que debemos considerar dos posibilidades en cuanto a la operación, una con el signo + y otra con el signo -.

La ecuación cuadrática puede tener las siguientes soluciones, de acuerdo al valor de la cantidad sub-radical, conocida como discriminante:

-Si b² – 4ac > 0, la ecuación cuadrática tiene dos soluciones reales y diferentes.

-Cuando b² – 4ac = 0, la ecuación tiene solución única, dada por:

x = -b/2a

-Finalmente, si b² – 4ac 0, la ecuación no tiene soluciones reales, pero sí tiene soluciones complejas.

Veamos algunos ejemplos en los cuales se aplica la fórmula general, notando que si alguno de los coeficientes que acompañan a la incógnita no aparece, se entiende que vale 1. Y si el término independiente es el que no se encuentra, entonces vale 0.

– Ejemplo 1

Resolver las siguientes ecuaciones cuadráticas:

a) 6x² + 11x -10 = 0

b) 3x² -5x -1 = 0

Respuesta a

Escribimos los coeficientes de cada término: a = 6, b = 11, c = -10 y sustituimos los valores en la fórmula general:

El resultado conduce a las siguientes dos soluciones reales:

x₁ = (-11 + 19)/12 = 8/12 = 2/3

x₂ = (-11 – 19)/12= -5/2

Respuesta b

Nuevamente se determinan los coeficientes: a = 3, b = -5 y c = -1. Al sustituir en la fórmula:

A diferencia del caso anterior, la raíz cuadrada de 37 no es un número entero, pero igualmente podemos plantear las dos soluciones y dejar la raíz o bien encontrar el valor decimal correspondiente con la ayuda de la calculadora:

x₁ = (-5 + √37)/6 ≈ 0.18

x₂ = (-5 – √37)/6 ≈ – 1.85

– Ejemplo 2

Resolver la ecuación de segundo grado x² – 4x +13 = 0.

Respuesta

Como siempre, identificamos los valores de los coeficientes y sustituimos en la fórmula general: a = 1, b = – 4, c = 13. Ello conduce a:

Tenemos una raíz negativa, por lo tanto las soluciones de esta ecuación son números complejos. La raíz se puede expresar en términos de i, la unidad imaginaria:

√(36i²) = 6i

Ya que i² = -1, por lo tanto las soluciones complejas son:

x₁ = (4 + 6i)/2 = 2 + 3i

x₂ = (4 – 6i)/2 = 2 – 3i

Ejercicio resuelto

Una escalera de 10 m de largo reposa apoyada contra una pared vertical, con el pie a 6 m de dicha pared. La escalera resbala y el pie se separa 3 m más de la base.

Hallar la distancia vertical que recorre el tope de la escalera.

Solución

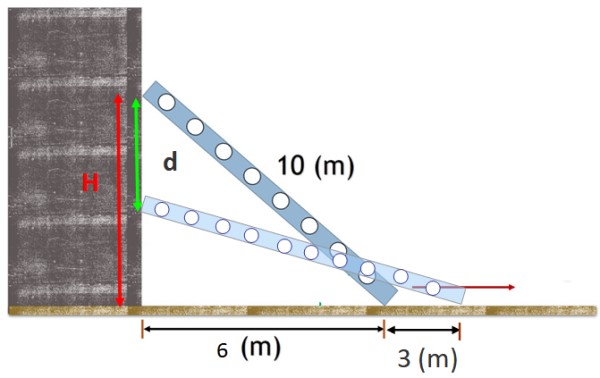
Para encontrar la distancia vertical que desliza el tope de la escalera, hay que encontrar la posición en que este se encontraba originalmente respecto al suelo. Lo podemos hacer con el teorema de Pitágoras, pues la figura que se forma es la de un triángulo rectángulo:

H = (10² – 6²) ^½ = 8 m

Una vez que la escalera resbala, se desplaza una distancia d, medida desde que el tope se encontraba a 8 m de altura, hasta llegar a su nueva posición, a (H-d) metros de altura sobre el suelo. La incógnita a despejar es d.

Para encontrarla planteamos un nuevo triángulo rectángulo, el que se forma después de que la escalera resbaló un poco. Este triángulo sigue teniendo hipotenusa igual a 10 m y el cateto paralelo al suelo mide ahora 6m + 3m = 9 m, por lo tanto:

(H-d)² = 10² – 9² = 100 – 81 = 19

Sustituimos H = 8m, calculado previamente:

(8-d)² = 19

La ecuación se puede resolver de varias maneras, incluyendo por supuesto el uso la fórmula general, el cual mostraremos a continuación con estos pasos:

Paso 1

Desarrollar el producto notable de la izquierda:

64 -16d + d² = 19

Paso 2

Establecer la ecuación de segundo grado para la incógnita d:

d² – 16d + 45 = 0

Paso 3

-Los coeficientes son: a = 1, b = -16 y c = 45, los sustituimos en la fórmula general:

Las soluciones de la ecuación son:

d₁ = (16 + √76)/2 ≈ 12.36 m

d₂ = (16 – √76)/2 ≈ 3.64 m

Paso 4

Se analizan las soluciones obtenidas: la primera de ellas no tiene sentido físico, ya que no es posible que la escalera resbale 12.36 m, si originalmente el tope estaba a 8 m de altura sobre el suelo.

Por lo tanto, la respuesta correcta es la segunda solución: el tope de la escalera resbala d = 3.64 m.

¿Puede el lector resolver el problema aplicando otro método?

Referencias

1. Baldor. 1977. Álgebra Elemental. Ediciones Cultural Venezolana.
2. Hoffman, J. Selección de temas de Matemática. Volumen 2.
3. Jiménez, R. 2008. Álgebra. Prentice Hall.
4. Stewart, J. 2006. Precálculo: Matemáticas para el Cálculo. 5ta. Edición. Cengage Learning.
5. Zill, D. 1984. Álgebra y Trigonometría. McGraw Hill.