Ley de los signos: qué es, suma, resta, multiplicación, división

¿Qué es la ley de los signos?

La ley de los signos es el conjunto de reglas utilizado en los cálculos aritméticos y algebraicos con números reales para asignar correctamente el signo al resultado, cuando están involucradas cantidades tanto positivas como negativas.

Hay reglas adecuadas según la operación que se lleve a cabo: suma, resta, multiplicación y división, que son las más básicas, y también existen reglas de signos relativas a las operaciones de potenciación y radicación.

En una operación dada, ya sea a mano o con calculadora, es preciso aplicar correctamente la ley de los signos para asegurar un resultado correcto, ya que apenas un pequeño cambio en los signos altera significativamente las cantidades.

A continuación se examina la ley de los signos para cada operación aritmética básica y los casos que se pueden presentar.

Ley de los signos en la suma

1) Si los números a sumar tienen igual signo

Los números se suman como de costumbre y al resultado se le agrega el signo de los números, sin importar si este es positivo o negativo.

Es importante tener presente que a los números positivos por lo general no se les antepone el signo, sino que se escriben directamente. En cambio, los números negativos se escriben entre paréntesis, sobre todo cuando van precedidos del símbolo de una operación aritmética, a fin de evitar confusiones.

Ejemplos de sumas de números con igual signo:

3 + 9 = 12
4 + 7 + 1 + 6 = 18
(−3) + (−8) = −11
(−5) + (−10) + (−6) = −21

2) Si los números a sumar tienen diferente signo

Los números se restan y al resultado se le agrega el signo del número que tenga mayor valor absoluto, ya sea positivo o negativo.

A modo de ejemplo efectuar la operación 5 + (−14). Como el valor absoluto de (−14) es mayor que el valor absoluto de 5, se le restan 5 unidades a 14, lo cual da 9 y a este resultado se le coloca signo negativo:

5 + (−14) = −9

Más ejemplos de esta regla aplicada a la suma de dos números de distinto signo son:

(−27) + 12 = −15

12 + (−7) = 5

Si en la operación hay más de dos sumandos con distintos signos, se puede aplicar la propiedad asociativa de la suma:

(−20) + 9 + (−7) = [(−20) + 9] + (−7)

Se realiza primero la operación en corchete, que consiste en la suma de dos números de diferente signo, para lo cual se aplica la regla descrita: se restan y el resultado lleva el signo del número con mayor valor absoluto:

(−20) + 9 = −11

La operación queda así:

(−20) + 9 + (−7) = (−11) + (−7)

Ahora se tiene la suma de dos números de igual signo, entonces se suman normalmente y al resultado se coloca un signo negativo:

(−20) + 9 + (−7) = (−11) + (−7) = −18

Ley de los signos en la resta

La resta de dos números se define como la suma del opuesto. A su vez el opuesto a un número es dicho número con el signo cambiado. Por ejemplo, el opuesto de 2 es (−2), el opuesto de (−5) es 5 y así sucesivamente.

Con esto en mente, cuando se tiene la resta de dos números:

a − b

Simplemente se transforma en la suma del opuesto de b:

a + (− b)

Y se procede tal como se describió en la sección anterior. Nótese que anteponer un signo + a un número negativo no lo altera, pero mucho cuidado, lo contrario no es cierto.

Cuando el número “a”, que es el minuendo, es mayor que el número “b”, que es el sustraendo, se opera como en la resta de números naturales. No hay problema, puesto que a un número grande se le está restando una cantidad menor:

25 − 8 = 17

Con los ejemplos que siguen, el método de sumar el opuesto para restar es muy conveniente:

(−5) − 24 = (−5) +(−24) = − 29
32 − (−23) = 32 + 23 = 55

Ley de los signos en la multiplicación

La ley de los signos en la multiplicación se aplica de esta forma:

• Al multiplicar dos números del mismo signo el resultado siempre es positivo.
• El producto de dos números de signo contrario siempre es negativo.

El resumen de la regla de los signos para la multiplicación se muestra en la imagen:

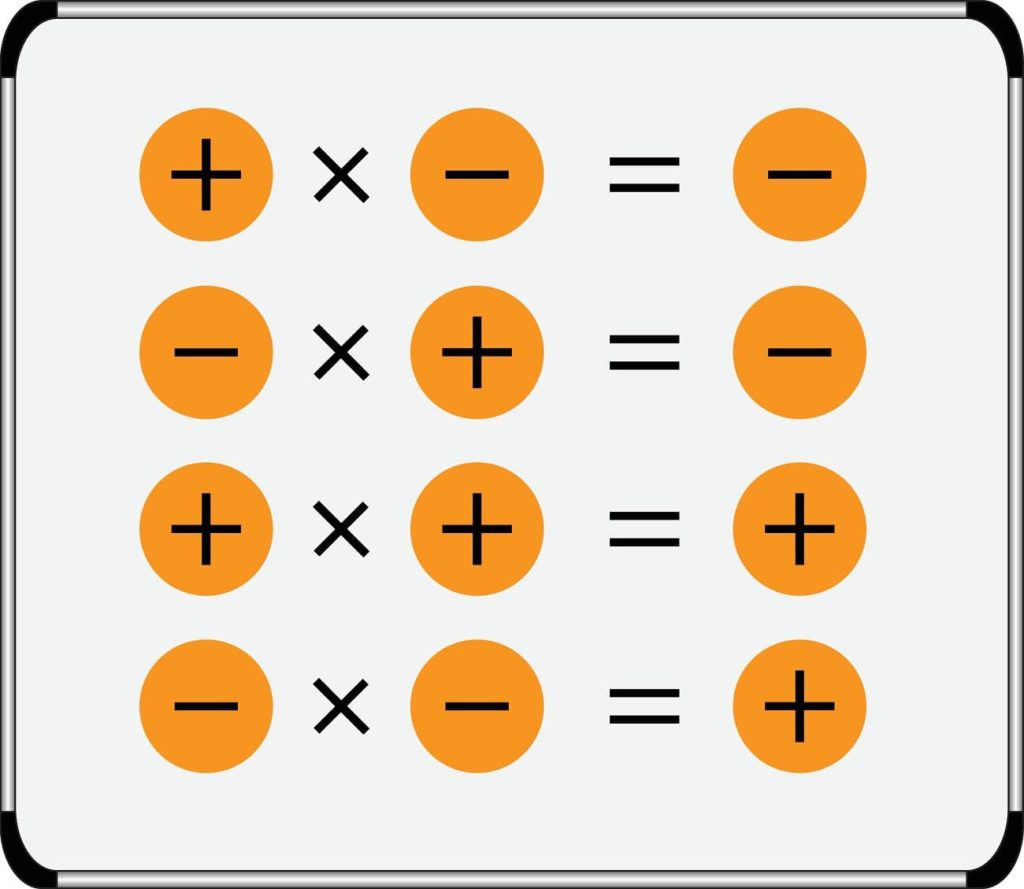
Obsérvese que los números positivos se pueden escribir sin el signo precedente, pero los números negativos siempre lo tienen, además dos símbolos aritméticos nunca se escriben uno seguido del otro, siempre deben estar separados por un paréntesis, por ejemplo:

Incorrecto: 3 × −4
Correcto: 3 × (−4)= −12

(−5) × 6 = −5 × 6 = −30
(−3) × (−11) = 33
10 × 27 = 270

Para multiplicar más de dos números, se hace uso de la propiedad asociativa de la multiplicación, ya que el orden de los factores no altera el producto, por ejemplo, al efectuar:

(−2) × (−14) ×16

Se puede multiplicar los dos primeros factores, o los dos últimos si se quiere, y luego multiplicar el resultado por el factor restante. En este caso se multiplicarán primero los dos factores comenzando por la izquierda:

[(−2) × (−14)] ×16

El producto de dos números negativos es positivo, luego (−2) × (−14) = 28 y queda:

28 ×16 = 448

Ley de los signos en la división

Es análoga a la regla de los signos para la multiplicación:

• El cociente de dos números del mismo signo siempre es positivo.
• Al dividir dos números de signo contrario, el resultado siempre es negativo.

Por ejemplo:

24 ÷ 8 = 3
−36 ÷ 3 = −12
162 ÷ (−9) = −18
−216 ÷ (−6) = 36

Ley de los signos en la potenciación y la radicación

Un número escrito con forma de exponente es:

aⁿ

Donde “a” es la base y “n” es el exponente. Se distinguen dos casos, de acuerdo a la paridad del exponente:

Caso 1: a es positiva

Cuando la base es positiva, el resultado es positivo sin importar si el exponente es par o impar, como en:

2³ = 8 
3⁴ = 81

Caso 2: a es negativa

Aquí se presentan dos casos:

• Cuando el exponente es par, entonces el resultado es positivo.
• Si el exponente es impar, es negativo.

Ejemplos

3² = 3∙3 = 9
2³ = 2∙2∙2 = 8
(−2)⁴ = (−2) ∙ (−2) ∙(−2) ∙(−2) = 16
(−3)³ = (−3)∙ (−3)∙ (−3) = −27

Operaciones con símbolos de agrupación

Con frecuencia aparecen operaciones separadas con símbolos de agrupación: paréntesis, corchetes y llaves. Estos se eliminan desde dentro hacia afuera teniendo en cuenta lo siguiente:

• Si un símbolo de agrupación está precedido por un signo positivo, se puede retirar sin cambiar los signos del contenido, por ejemplo: + (−3 + 5 − 1) = −3 + 5 − 1 = 1.
• Si al símbolo de agrupación le precede un signo negativo, se retira invirtiendo el signo del contenido, por ejemplo: − (−3 + 5 −1) = 3 − 5 + 1 = −1.
• Cuando existan operaciones combinadas de suma, resta, multiplicación y división, se puede hacer uso de las propiedades asociativa y distributiva a conveniencia.

Ejercicios resueltos

a) 10 + 10

Solución: 20

b) (-8) + (-3)

Solución: -11

c) (3) + (-10) 

Solución: -7

d) (5) x (-3)

Solución: -15

e) (-10) x (-10)

Solución: 100

f) (18)÷(-3)

Solución: -6

g) (-10)÷(-2)

Solución: 5

h) 4 − (− 7 + 9)

Solución: 4 − (− 7 + 9) = 4 + 7 − 9 = 11− 9 = 2