Historia de la trigonometría desde sus orígenes
La historia de la trigonometría se refiere al conjunto de hechos y avances que ocurrieron en torno a esta rama de las matemáticas desde sus orígenes hasta los acontecimientos más recientes.
Al realizar un breve viaje a través de su historia, se evidencia que esta ciencia nació como respuesta a los problemas que enfrentaron los antiguos astrónomos y navegantes para analizar el desplazamiento de las estrellas en el firmamento.

Así mismo, la palabra trigonometría surge de la composición de dos vocablos griegos: trigonon (triángulo) y metron (medida). El término aparece por primera vez en el libro Trigonometriae libri quinque, escrito por el matemático y científico alemán Pitiscus Bartolomé (1561-1613).
De esta forma, la etimología de la palabra muestra que la trigonometría es el estudio las relaciones existentes entre los ángulos de un triángulo y los segmentos o líneas que lo forman.
Índice del artículo
Los primeros pasos de la trigonometría fueron realizados por el hombre al verse impulsado por la necesidad de conocer y analizar el movimiento de las estrellas.
Es decir, el ser humano ideó la trigonometría porque se halló en situaciones donde era imposible hacer mediciones de manera directa, ya que para calcular los astros se requería de herramientas matemáticas más complejas.

Los estudios muestran que hace más de 3.000 años los babilonios ya manejaban el concepto de ángulo y de razones trigonométricas, es decir, eran capaces de establecer las relaciones entre los lados y los ángulos de los triángulos.
Por ejemplo, una tablilla de barro −escrita por los de babilonios− denominada Plimpton 322 (1800 a. C.) muestra una sucesión de columnas y filas que contienen números en escritura cuneiforme. Según las investigaciones realizadas por algunos expertos, esta tablilla representa lo que parecen ser una serie de funciones trigonométricas.
Los babilonios estaban familiarizados con los conceptos que dieron origen al teorema de Pitágoras (569-474 a.C) y entendían su principio.
De igual forma, conocían también el teorema atribuido a Tales de Mileto (695-546 a.C), el cual indica que toda recta, trazada de forma paralela a un lado de un triángulo, forma con los otros dos lados otro triángulo que es parecido al triángulo inicial.

Aunque no es apropiado hablar de trigonometría en el ámbito general de la matemática egipcia, no cabe duda que esta civilización manejaba ciertos conceptos trigonométricos.
Esto sucede porque al contemplar las grandes edificaciones que realizaron los egipcios, como son las pirámides, se puede concluir que disponían de algunos conocimientos sobre trigonometría.
Una dificultad de ingeniería básica que enfrentaron los egipcios −y que resolvieron asombrosamente− fue mantener la pendiente de forma uniforme en cada una de las caras de las pirámides (vale recordar que las caras de las pirámides tienen forma triangular).
Para esto utilizaban un concepto que llamaron “seqt” y que equivale a lo que entendemos hoy como pendiente de una superficie plana inclinada.
Además, los egipcios para realizar mediciones en las superficies verticales utilizaban como unidad el “codo” y en las horizontales la “mano”, que correspondía a 1/7 del codo. De esta manera calcularon los seqt o pendientes en las distintas edificaciones. Por ejemplo, en la pirámide de Jufú (Queope) el seqt es 5 1/2 manos por codo.
Todos los conocimientos de los babilonios y los antiguos egipcios pasaron a Grecia, donde se destacó el matemático y astrónomo Hiparco de Nicea (190-120 a. C), el cual es considerado como el padre de la trigonometría. Hiparco creó las tablas de “cuerdas”, con las cuales lograba resolver los problemas de triángulos planos.
Para confeccionarlas utilizó una circunferencia con un radio determinado (un radio es la distancia entre el centro de un círculo y cualquier punto de la circunferencia).
Luego, fue desplazando el radio para definir distintos ángulos; mientras hacía esto iba apuntando en la tabla la longitud de la línea que quedaba delimitada por los lados del ángulo y la circunferencia.
Estas “cuerdas” resultaron ser las precursoras de las tablas de las funciones trigonométricas que utilizamos en la actualidad.
Al igual que los estudiosos de Grecia, los astrónomos de la India también desarrollaron un sistema trigonométrico, pero a diferencia de los griegos estos astrónomos basaron sus análisis en la función “seno” en vez de utilizar las cuerdas.
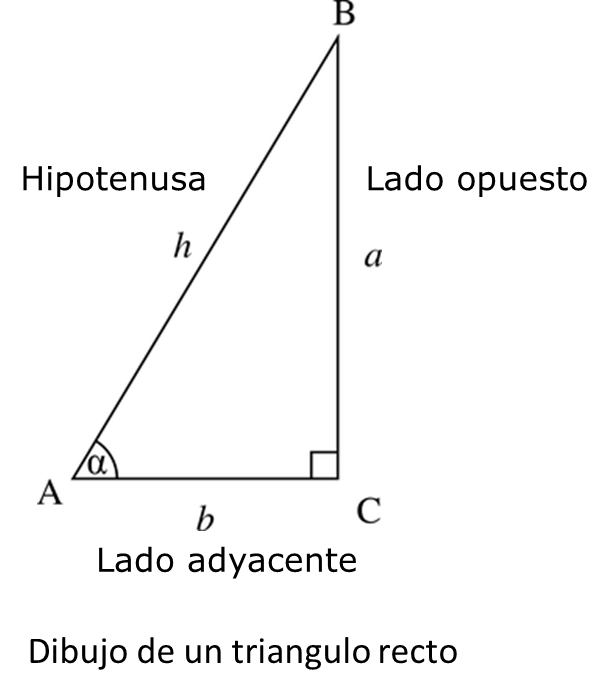
Sin embargo, la función “seno” expresada por estos astrónomos no es la utilizada en la actualidad; esta función no era una proporción (como se usa hoy en día), sino la longitud del lado opuesto a un ángulo de un triángulo rectángulo cuya hipotenusa se conoce.
A finales del siglo VIII los astrónomos árabes, influenciados por los estudios de trigonometría realizados por los pueblos de Grecia y la India, iniciaron importantes estudios sobre las relaciones entre los ángulos y sus lados.
De esta forma, a finales del siglo X plantearon las conocidas funciones de seno, coseno, tangente, cotangente, secante y cosecante.
También descubrieron y comprobaron teoremas primordiales de la trigonometría, los cuales son utilizados en los análisis de los triángulos planos y esféricos. Además, los matemáticos árabes sugirieron el uso del valor uno (“1”) para el radio (r = 1), lo cual dio lugar a los valores modernos de las funciones trigonométricas.

Las matemáticas de Occidente, específicamente entre los siglos XII y XV, estuvieron fuertemente influenciadas por los postulados de la Antigua Grecia, de la India y de los árabes.
Durante este tiempo fueron determinantes −en el área de la trigonometría− los aportes de Johann Müller, también conocido como Regiomontanus (1436-1476). Este matemático logró la sistematización y la generalización de métodos trigonométricos utilizados en el área de la geometría.
Regiomontanus elaboró y publicó un tratado que llamó De Triangulis Omnimodis Libri Quinque, el cual estaba constituido por cinco libros y un total de 131 páginas.
En este libro reglamentó todos los conceptos de trigonometría plana y esférica, los cuales fueron utilizados posteriormente por importantes astrónomos como: Nicolás Copérnico (1473-1543), Georg Joachim von Lauchen Réticos (1514-1574) y Pedro Nunes (1502-1578).
Durante el siglo XVII prosperaron los estudios sobre los cálculos trigonométricos gracias a los aportes de matemáticos como el escocés John Napier (1550-1617), quien planteó diversos métodos para la resolución de triángulos esféricos.

Más tarde, en el siglo XVIII fueron determinantes los aportes del matemático suizo Leonhard Euler (1707-1783), ya que sus estudios sentaron las bases de la trigonometría moderna al introducir la notación que se utiliza actualmente para las funciones trigonométricas.
Además, Euler logró definir la función exponencial y descubrió su relación con las funciones trigonométricas, lo cual le permitió describir las características de la trigonometría.
Posteriormente, Sir Isaac Newton (1643-1727), al inventar el cálculo diferencial e integral, facilitó la representación de un gran número de funciones matemáticas, entre las cuales están las trigonométricas. De esta manera la trigonometría pasó a formar parte del análisis matemático, donde hoy juega un papel fundamental.
- Mansfield, Daniel. Wildberger, N. (2017). Plimpton 322 is Babylonian exact sexagesimal trigonometry. Recuperado el 20 de mayo 2020 de: sciencedirect.com
- Jimenez S. (2017). Historia de la trigonometría y sus aplicaciones. Recuperado el 23 de mayo 2020 deedu
- Pérez, V. (2010). Historia de la trigonometría. Recuperado el 22 de mayo 2020 de: laguia2000.com
- S.A. (s.f.) Trigonometria. Recuperado el 23 de mayo 2020 de: blogspot.com
- Merlet, Jean-Pierre (2004). A Note on the History of Trigonometric Functions. Recuperado el 22 de mayo 2020 de: net
- Adamek, T., Penkalski, K., Valentine, G. (2005). The History of Trigonometry. Recuperado el 23 de mayo 2020 de: citeseerx.ist.psu.edu/
