Frecuencia absoluta: fórmula, cálculo, distribución, ejemplo
La frecuencia absoluta se define como la cantidad de veces que un mismo dato se repite dentro del conjunto de observaciones de una variable numérica. La suma de todas las frecuencias absolutas equivale a totalizar los datos.
Cuando se tienen muchos valores de una variable estadística, conviene organizarlos apropiadamente para extraer información sobre su comportamiento. Tal información viene dada por las medidas de tendencia central y las medidas de dispersión.
En los cálculos de estas medidas, los datos son representados a través de la frecuencia con que aparecen en la totalidad de las observaciones.
El ejemplo siguiente muestra lo reveladora que es la frecuencia absoluta de cada dato. Durante la primera quincena de mayo, estas fueron las tallas de trajes de cocktail más vendidas, de un conocido almacén de ropa para damas:
8; 10; 8; 4; 6; 10; 12; 14; 12; 16; 8; 10; 10; 12; 6; 6; 4; 8; 12; 12; 14; 16; 18; 12; 14; 6; 4; 10; 10; 18
¿Cuántos vestidos se venden de una talla en particular, por ejemplo la talla 10? A los dueños les interesa saberlo para hacer los pedidos.
Ordenando los datos resulta más fácil contar, hay exactamente 30 observaciones en total, que ordenadas de la talla menor a la mayor quedan así:
4;4; 4; 6; 6; 6; 6; 8; 8; 8; 8; 10; 10; 10; 10; 10; 10; 12; 12; 12; 12; 12; 12;14; 14; 14;16;16; 18; 18
Y ahora es evidente que la talla 10 se repite 6 veces, por lo tanto su frecuencia absoluta es igual a 6. El mismo procedimiento se lleva a cabo para averiguar la frecuencia absoluta de las restantes tallas.
Índice del artículo
- 1 Fórmulas
- 2 ¿Cómo sacar la frecuencia absoluta?
- 3 Distribución de frecuencias
- 4 Ejemplo
- 5 Ejercicio resuelto
- 6 Referencias
La frecuencia absoluta, denotada como fi, es igual al número de veces que determinado valor Xi está dentro del grupo de observaciones.
Suponiendo que el total de observaciones es de N valores, la sumatoria de todas las frecuencias absolutas debe ser igual a dicho número:
∑fi = f1 + f2 + f3 +… fn = N
Si cada valor de fi se divide entre el número total de datos N, se tiene la frecuencia relativa fr del valor Xi:
fr = fi / N
Las frecuencias relativas son valores comprendidos entre 0 y 1, porque N siempre es mayor a cualquier fi, pero la suma debe ser igual a 1.
Multiplicando por 100 a cada valor de fr se tiene la frecuencia relativa porcentual, cuya suma es 100%:
Frecuencia relativa porcentual = (fi / N) x 100%
También es importante la frecuencia acumulada Fi hasta una determinada observación, esta es la suma de todas las frecuencias absolutas hasta dicha observación inclusive:
Fi = f1 + f2 + f3 + … fi
Si la frecuencia acumulada se divide entre el número total de datos N, se tiene la frecuencia relativa acumulada, que multiplicada por 100 da como resultado la frecuencia relativa acumulada porcentual.
Para encontrar la frecuencia absoluta de un determinado valor que pertenece a un conjunto de datos, se organizan todos ellos de menor a mayor y se cuenta cuántas veces aparece el valor.
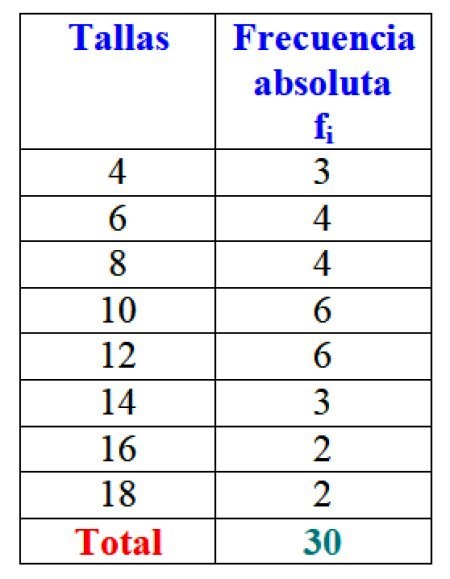
En el ejemplo de las tallas de los vestidos, la frecuencia absoluta de la talla 4 es de 3 vestidos, es decir f1 = 3. Para la talla 6, se vendieron 4 vestidos: f2 = 4. En la talla 8 también se vendieron 4 vestidos, f3 = 4 y así sucesivamente.
El total de resultados se puede representar en una tabla que muestre las frecuencias absolutas de cada una:
Evidentemente es ventajoso ordenar la información y poder acceder de un vistazo a ella, en vez de trabajar con los datos sueltos.
Importante: obsérvese que al sumar todos los valores de la columna fi siempre se obtiene el número total de datos. Si no es así hay que revisar la contabilidad, ya que hay un error.
La tabla anterior se puede extender agregando los otros tipos de frecuencia en sucesivas columnas a la derecha:
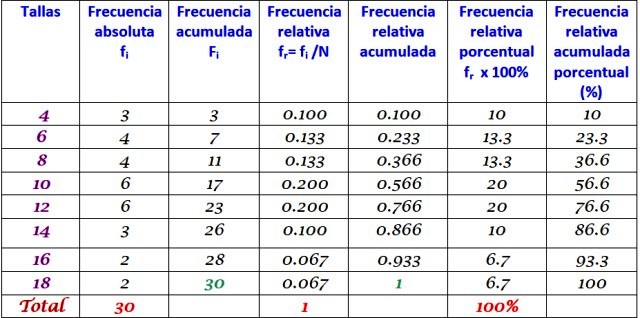
La distribución de frecuencias es el resultado de organizar los datos en términos de sus frecuencias. Cuando se trabaja con muchos datos, es conveniente agruparlos en categorías, intervalos o clases, cada una de ellas con sus respectivas frecuencias: absoluta, relativa, acumulada y porcentual.
El objetivo de hacerlas es acceder más fácilmente a la información que contienen los datos, así como interpretarlos adecuadamente, lo cual no es posible cuando se presentan sin orden.
En el ejemplo de las tallas, los datos no están agrupados, ya que no son demasiadas tallas y se pueden manipular y contabilizar fácilmente. Las variables cualitativas también se pueden trabajar de esta manera, pero cuando los datos son muy numerosos, se trabaja mejor agrupándolos en clases.
Para agrupar los datos en clases de igual tamaño, hay que considerar lo siguiente:
-Tamaño, ancho o amplitud de clase: es la diferencia entre el mayor valor de la clase y el menor.
El tamaño de la clase se decide dividiendo el rango R entre el número de clases a considerar. El rango es la diferencia entre el máximo valor de los datos y el menor, así:
Tamaño de clase = Rango / Número de clases.
-Límite de clase: intervalo que va desde el límite inferior hasta el límite superior de la clase.
-Marca de clase: es el punto medio del intervalo, que se considera representativo de la clase. Se calcula con la semisuma del límite superior y el límite inferior de la clase.
–Cantidad de clases: se puede emplear la fórmula de Sturges:
Número de clases = 1 + 3,322 log N
Donde N es el número de clases. Como suele ser un número decimal se redondea al entero siguiente.
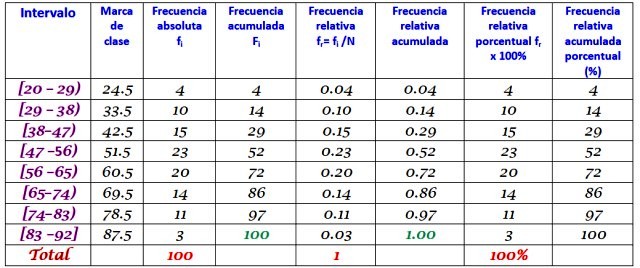
Una máquina de una gran fábrica está fuera de operación, ya que presenta fallas recurrentes. Los lapsos de tiempo consecutivos de inactividad en minutos, de dicha máquina, se registran a continuación, con un total de 100 datos:
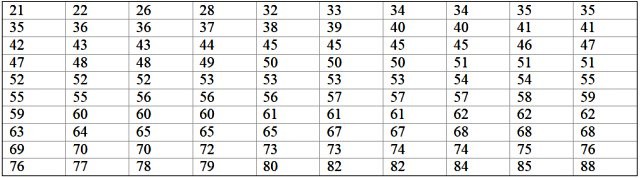
Primero se determina el número de clases:
Número de clases = 1 + 3,322 log N = 1 + 3.32 log 100 = 7.64 ≈ 8
Tamaño de clase = Rango / Número de clases = (88-21) / 8 = 8.375
También es un número decimal, por lo que se toma 9 como tamaño de clase.
La marca de clase es el promedio entre el límite superior y el inferior de la clase, por ejemplo para la clase [20-29) se tiene una marca de:
Marca de clase = (29 + 20) / 2 = 24.5
Se procede del mismo modo para encontrar las marcas de clase de los intervalos restantes.
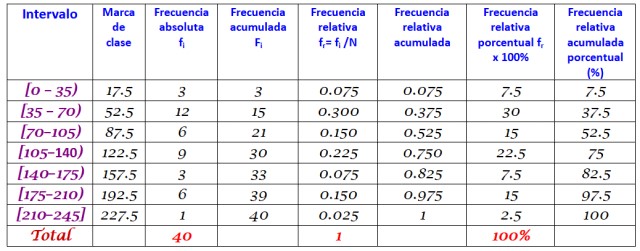
40 jóvenes indicaron que el tiempo en minutos que pasaron en internet el domingo pasado fue el siguiente, ordenado de forma creciente:
0; 12; 20; 35; 35; 38; 40; 45; 45, 45; 59; 55; 58; 65; 65; 70; 72; 90; 95; 100; 100; 110; 110; 110; 120; 125; 125; 130; 130; 130; 150; 160; 170; 175; 180; 185; 190; 195; 200; 220.
Se pide construir la distribución de frecuencias de estos datos.
El rango R del conjunto de N = 40 datos es:
R = 220 – 0 = 220
La aplicación de la fórmula de Sturges para determinar la cantidad de clases arroja el resultado siguiente:
Número de clases = 1 + 3,322 log N = 1 + 3.32 log 40 = 6.3
Como es un decimal, el entero inmediato es 7, por lo tanto los datos se agrupan en 7 clases. Cada clase tiene un ancho de:
Tamaño de clase = Rango / Número de clases = 220/7 = 31.4
Un valor cercano y redondo es 35, por lo tanto se elige un ancho de clase de 35.
Las marcas de clase se calculan promediando el límite superior y el inferior de cada intervalo, por ejemplo, para el intervalo [0,35):
Marca de clase = (0+35)/2 = 17.5
Se procede del mismo modo con las restantes clases.
Por último, las frecuencias se calculan según el procedimiento descrito antes, resultando en la siguiente distribución:
- Berenson, M. 1985. Estadística para administración y economía. Interamericana S.A.
- Devore, J. 2012. Probability and Statistics for Engineering and Science. 8th. Edition. Cengage.
- Levin, R. 1988. Estadística para Administradores. 2da. Edición. Prentice Hall.
- Spiegel, M. 2009. Estadística. Serie Schaum. 4 ta. Edición. McGraw Hill.
- Walpole, R. 2007. Probabilidad y Estadística para Ingeniería y Ciencias. Pearson.
