Simetría central: propiedades, ejemplos y ejercicios
Dos puntos A y A’ tienen simetría central respecto de un punto O cuando el segmento AA’ pasa por él y además es el punto medio de AA’. Al punto O se le denomina centro de simetría.
El simétrico central de un triángulo ABC respecto de un punto O, es otro triángulo A’B’C’ que tiene las siguientes características:
-Los segmentos homólogos son de igual longitud
-Sus ángulos correspondientes tienen la misma medida.
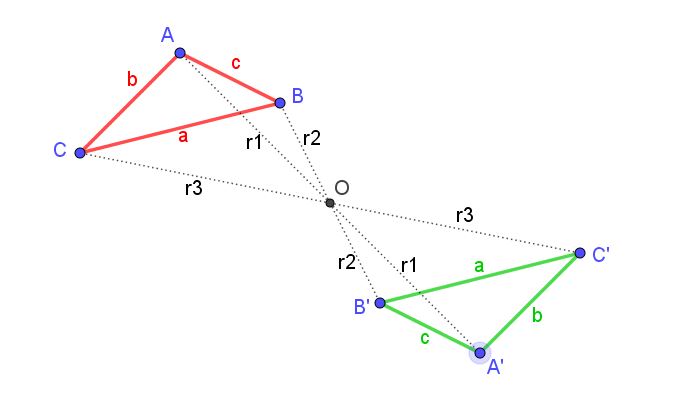
En la figura 1 puede verse un triángulo ABC (de color rojo) y su simétrico central A’B’C’ (de color verde), respecto al centro de simetría O.
En esta misma figura, un observador atento se daría cuenta de que se obtiene el mismo resultado aplicando una rotación del triángulo original, con tal de que sea de 180º y esté centrada en O.
Por lo tanto, una simetría central es equivalente a un giro de 180º respecto al centro de simetría.
Índice del artículo
Una simetría central tiene las siguientes propiedades:
-El centro de simetría es el punto medio del segmento que une un punto con su simétrico.
-Un punto simétrico de otro que esté ubicado en el centro de simetría, coincide con el centro de simetría.
-El simétrico central de un triángulo es un triángulo congruente (igual) al original.
-La imagen por simetría central de una circunferencia es otra circunferencia de igual radio.
-Una circunferencia tiene simetría central respecto a su propio centro.

-La elipse tiene simetría central respecto a su centro.
-Un segmento posee simetría central respecto de su punto medio.
-El triángulo equilátero no tiene simetría central respecto de su centro, porque su simétrico, aunque congruente al primero, da un triángulo equilátero girado.
-Los cuadrados tienen simetría central respecto de su centro.
-Un pentágono carece de simetría central respecto de su centro.
-Polígonos regulares tienen simetría central cuando tienen número de lados par.
Los criterios de simetría tienen muchas aplicaciones en ciencias e ingeniería. La simetría central está presente en la naturaleza, por ejemplo cristales de hielo y telarañas tienen esta clase de simetría.
Además, muchos problemas se resuelven fácilmente cuando se aprovecha la existencia de la simetría central y otras clases de simetría. Por ello es conveniente identificar rápidamente cuando se presenta.

Dado un punto P de coordenadas (a, b), hay que hallar las coordenadas de su simétrico P´ respecto del origen O de coordenadas (0, 0).
Lo primero es construir el punto P’, para lo cual se traza una recta que pase por el origen O y por el punto P. La ecuación de dicha recta es y = (b/a) x.
Ahora llamemos (a’, b’) las coordenadas del punto simétrico P’. El punto P’ debe estar sobre la recta que pasa por O y por lo tanto se cumple: b’ = (b/a) a’. Además la distancia OP debe ser igual a OP’, lo que en forma analítica se escribe así:
√( a2 + b2) = √( a’2 + b’2 )
Lo siguiente es sustituir b’ = [(b/a).a’] en la expresión anterior y elevar al cuadrado a ambos lados de la igualdad para eliminar la raíz cuadrada: (a2 + b2) = [a’2 + (b2/a2).a’2]
Al extraer factor común y simplificar, se llega a que a’2 = a2. Esta ecuación tiene dos soluciones reales: a’ = +a o bien a’ = -a.
Para obtener b’, usamos nuevamente b’ = (b/a) a’. Si se sustituye la solución positiva de a’ se llega a que b’ = b. Y cuando se sustituye la solución negativa, entonces b’ = -b.
La solución positiva da para P’ el mismo punto P, por lo que queda descartada. La solución negativa ofrece definitivamente las coordenadas del punto simétrico:
P’: (-a, -b)
Se requiere demostrar que un segmento AB y su simétrico central A’B’ tienen la misma longitud.
Comenzando con las coordenadas del punto A, que son (Ax, Ay) y las del punto B: (Bx, By), la longitud del segmento AB viene dada por:
d(AB) = √( (Bx – Ax)2 + (By – Ay)2 )
Por analogía, el segmento simétrico A’B’ tendrá longitud dada por:
d(A’B’) = √( (Bx’ – Ax’)2 + (By’ – Ay’)2 )
Las coordenadas del punto simétrico A’ son Ax’ = -Ax y Ay’ = -Ay. Similarmente las de B’ son Bx’ = -Bx y By’ = -By. Si estas coordenadas se sustituyen en la ecuación de la distancia d(A’B’) se tiene:
d(A’B’) = √( (-Bx + Ax)2 + (-By + Ay)2) que es equivalente a:
√( (Bx – Ax)2 + (By – Ay)2) = d(AB)
Quedando demostrado así que ambos segmentos tienen la misma longitud.
Demuestre en forma analítica que el simétrico central O de una circunferencia de radio R y centro O, es la misma circunferencia original.
Solución
La ecuación de una circunferencia de radio R y centro O(0,0) es:
x2 + y2 = R2 (Ecuación de la circunferencia C)
Si a cada punto P de la circunferencia y de coordenadas (x, y) se le encuentra su simétrico P’ de coordenadas (x’, y’), la ecuación de la circunferencia simétrica es:
x’2 + y’2 = R2 (Ecuación de la circunferencia simétrica C’)
Ahora nos remitimos al resultado del ejemplo 1, en el que se concluye que las coordenadas de un punto P’, simétrico a P y de coordenadas (a,b), es (-a,-b).
Pero en este ejercicio, el punto P tiene coordenadas (x, y), por lo que su simétrico P’ tendrá coordenadas x’ = -x e y’ = -y. Sustituyendo esto en la ecuación de la circunferencia simétrica se tiene:
(-x)2 + (-y)2 = R2
Lo cual es equivalente a: x2+ y2 = R2, concluyendo que el simétrico central de una circunferencia respecto a su centro es la propia circunferencia.
Demostrar en forma geométrica que la simetría central preserva los ángulos.
Solución
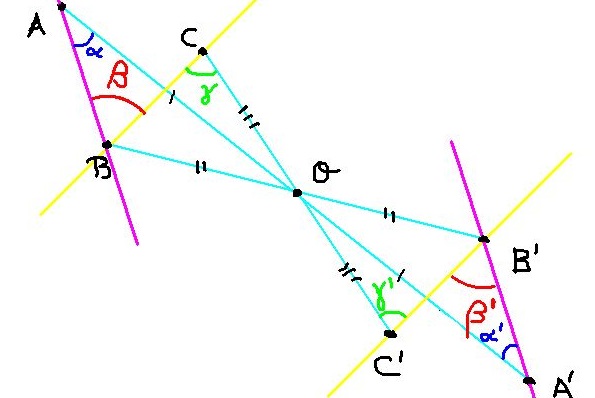
Se tienen tres puntos A, B y C sobre el plano. Se construyen sus simétricos A’, B’ y C’ con respecto al centro de simetría O, tal como se muestra en la figura 4.
Ahora hay que demostrar que el ángulo ∡ABC = β tiene la misma medida que el ángulo ∡A’B’C’ = β’.
Como C y C’ son simétricos, entonces OC = OC’. Similarmente OB = OB’ y OA = OA’. Por otra parte, el ángulo ∡BOC = ∡B’OC’ por ser opuestos por el vértice.
Luego los triángulos BOC y B’OC’ son congruentes por tener un ángulo igual entre dos lados iguales.
Debido a que BOC es congruente a B’OC’ entonces los ángulos γ y γ’ son iguales. Pero estos ángulos, además de cumplir γ = γ’ son alternos internos entre las rectas BC y B’C’ lo que implica que la recta BC es paralela a B’C’.
Similarmente BOA es congruente a B’OA’ de lo que se sigue que α = α’ . Pero α y α’ son ángulos alternos internos entre las rectas BA y B’A’, de lo que se concluye que la recta BA es paralela a B’A’.
Como el ángulo ∡ABC = β tiene sus lados paralelos con el ángulo ∡A’B’C’ = β’ y además ambos son agudos se concluye que:
∡ABC = ∡A’B’C’ = β = β’
Demostrándose de esta forma, que la simetría central conserva la medida de los ángulos.
- Baldor, J. A. 1973.Geometría plana y del espacio. Cultural Centroamericana.
- Leyes y fórmulas matemáticas. Sistemas de medida de ángulos. Recuperado de: ingemecanica.com.
- Wentworth, G. Plane Geometry. Recuperado de: gutenberg.org.
- Wikipedia. Simetría central. Recuperado de: es.wikipedia.com
- Wikipedia. Transportador. Recuperado de: es.wikipedia.com
- Zapata F. Ángulos conjugados internos y externos. Recuperado de: lifeder.com
