Triángulos oblicuángulos: características, ejemplos, ejercicios

Los triángulos oblicuángulos son los que no tienen ningún ángulo recto, por lo tanto ninguno de sus ángulos internos es igual a 90º. Entonces, un triángulo oblicuángulo puede ser acutángulo u obtusángulo.

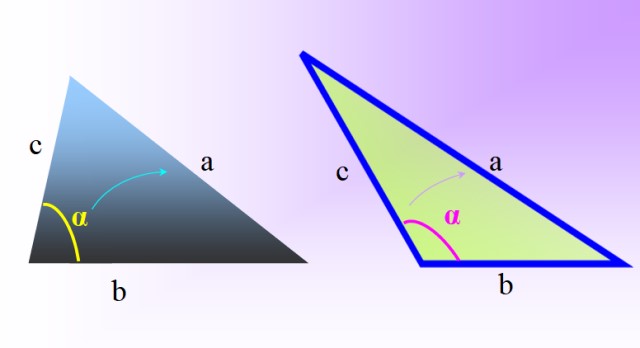
En el primer caso, los ángulos internos del triángulo son agudos o lo que es igual: menores a 90º, mientras que en el segundo, hay siempre un ángulo mayor a 90º, o sea, un ángulo obtuso. Veamos un ejemplo de cada uno en la siguiente figura:

Para encontrar las longitudes de los lados y las medidas de los ángulos internos de esta clase de triángulos, en ausencia de ángulos rectos no es posible aplicar el teorema de Pitágoras.

Sin embargo, existen alternativas para resolver el triángulo: los teoremas del coseno y del seno y el hecho de que la suma de los ángulos internos es igual a 180º.

Índice del artículo

• 1 Ejemplos de triángulos oblicuángulos
  • 1.1 Triángulo acutángulo
  • 1.2 Triángulo obtusángulo
• 2 Teoremas del seno y del coseno
  • 2.1 Teorema del seno
  • 2.2 Teorema del coseno
• 3 Ejercicios resueltos
  • 3.1 – Ejercicio 1
  • 3.2 – Ejercicio 2
  • 3.3 – Ejercicio 3
  • 3.4 – Ejercicio 4
  • 3.5 – Ejercicio 5
  • 3.6 – Ejercicio 6
• 4 Referencias

Ejemplos de triángulos oblicuángulos

Guiándonos por la figura 1, podemos reconocer fácilmente los triángulos oblicuángulos mediante dos criterios que daremos a continuación.

Triángulo acutángulo

Sea el triángulo de lados a, b y c, con α el ángulo frente al lado a.

Si el cuadrado del lado a opuesto al ángulo agudo α, es menor que la suma de los cuadrados de los lados restantes, el triángulo es acutángulo. Algebraicamente:

a² b² + c²; α 90º

El familiar triángulo equilátero, aquel que tiene sus tres lados de la misma medida, es acutángulo y por ende oblicuángulo, ya que sus ángulos internos son iguales y miden 60º.

Triángulo obtusángulo

En cambio, si el cuadrado del lado opuesto a al ángulo obtuso α es mayor que la suma de los cuadrados de los otros dos, estamos en presencia de un triángulo obtusángulo. Por lo tanto:

a² > b² + c²; α > 90º

Por ejemplo, un triángulo cuyos ángulos internos sean 105º, 60º y 15º es un triángulo oblicuángulo obtusángulo. Nótese que 105º + 60º + 15º = 180º.

Teoremas del seno y del coseno

Para resolver los triángulos oblicuángulos, es decir, encontrar las medidas de todos sus lados y todos sus ángulos, se requieren los teoremas del seno y del coseno.

Sean a, b y c los lados de un triángulo, y α, β y γ sus ángulos internos. Entonces:

Teorema del seno

El teorema del seno establece lo siguiente:

Donde α es el ángulo opuesto al lado a, β es el ángulo opuesto al lado b y γ es el ángulo que está enfrente al lado c.

De manera equivalente:

Escogemos aplicar el teorema del seno cuando vamos a resolver un triángulo del que se conocen más ángulos que lados.

Teorema del coseno

De acuerdo al teorema del coseno:

c² = a² + b² – 2⋅a⋅b⋅cos γ

Nuevamente el ángulo γ se encuentra enfrente del lado c. Asimismo, podemos escribir expresiones equivalentes para los lados a y b, de la siguiente manera:

a² = b² + c² – 2⋅b⋅c⋅cos α

Y

b² = a² + c² – 2⋅a⋅c⋅cos β

El teorema del coseno se aplica de preferencia cuando se conoce el valor de dos lados y el ángulo entre ellos. Asimismo, una vez conocidos los tres lados de un triángulo, el teorema nos permite calcular el coseno del ángulo entre dos de ellos.

Ejercicios resueltos

– Ejercicio 1

Comprobar que el triángulo cuyos lados miden 20, 10 y 12 unidades arbitrarias es obtusángulo.

Solución

No conocemos ninguno de los ángulos internos, pero atendiendo al criterio que sirve para reconocer triángulos obtusángulos, podemos plantear las desigualdades con los cuadrados de los lados para observar si se cumple.

Primero hallamos los cuadrados de cada lado:

20² = 400

10² = 100

12² = 144

Y vemos que en efecto: 400 > 100 + 144, ya que 400 > 244. Por lo tanto, el triángulo contiene un ángulo mayor a 90º, ubicado frente al lado que mide 20. En consecuencia, este triángulo, además de ser oblicuángulo, también es obtusángulo.

– Ejercicio 2

Dado el triángulo oblicuángulo mostrado en la figura 2, cuyas medidas están dadas en unidades arbitrarias, determinar:

a) El valor de x. ¿Es un triángulo acutángulo u obtusángulo?

b) Los restantes ángulos internos del triángulo

c) Perímetro

d) Área.

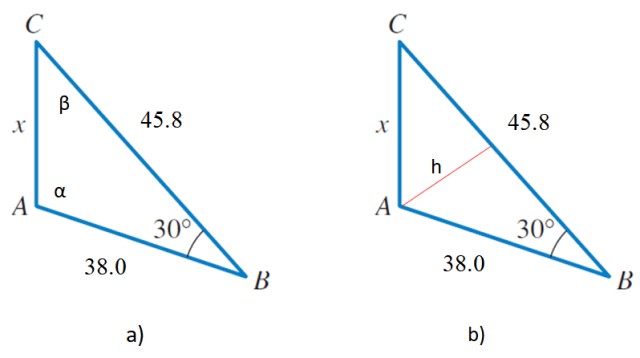
Solución a

Del triángulo se conocen dos lados adyacentes, cuyas medidas son 38.0 y 45.8 y el ángulo entre ellos, que es 30º, por lo tanto el teorema del coseno es de aplicación inmediata:

x² = 38.0² + 45.8² – 2 x 38.0 x 45.8 x cos 30º = 527.18

Por lo tanto:

x = (527.18)^1/2 = 22.96

El dibujo sugiere que α > 90º y el triángulo es obtusángulo, además de oblicuángulo. Para comprobarlo, hallamos los cuadrados de los lados, como se hizo en el ejercicio anterior:

22.96² = 527.18

38.0² = 1444.00

45.8² =  2097.64

El ángulo α es mayor que 90º si se cumple que el cuadrado del lado opuesto: 45.8²  es mayor que la suma de los cuadrados de los otros lados, la cual es 22.96² + 38.0².

Veamos si ocurre así:

527.18 + 1444.00 = 1971.2

En efecto:

2097.64 >1971.2

Por consiguiente el ángulo α es mayor a 90º.

Solución b

Ahora podemos aplicar el teorema del seno para encontrar uno de los ángulos faltantes. Vamos a plantearlo para el ángulo β:

sen 30º / 22.96 = sen β / 38

sen β = 38 x (sen 30º / 22.96) = 0.8275

β = arcsen (0.8275) = 55.84º

El ángulo faltante lo podemos encontrar sabiendo que la suma de los ángulos internos de cualquier triángulo es 180º. Por lo tanto:

55.84º  + 30º + α = 180º

α = 94.16º

Si se prefiere, también se puede emplear el teorema del coseno para encontrar el coseno del ángulo que se encuentra entre dos lados adyacentes cualesquiera. Una vez obtenido, se utiliza la función arco coseno para determinar el ángulo.

Los resultados pueden diferir un poco en los decimales, según el redondeo llevado a cabo.

Solución c

El perímetro P es el contorno de la figura, equivalente a la suma de las medidas de los tres lados:

P = 22.96 + 38.00 + 45.80 = 106.76 unidades arbitrarias.

Solución d

La fórmula para calcular el área de un triángulo cualquiera es:

A = (1/2) x base x altura

Necesitamos escoger uno de los lados como base y determinar la altura. Por ejemplo, escogiendo el lado que mide 45.8, trazamos la altura h hasta el vértice A, que es la línea roja en la figura 2b.

Al hacer esto dividimos el triángulo original en dos triángulos rectángulos, ambos con h como cateto en común. Cualquiera de ellos sirve, ya que conocemos un lado y un ángulo agudo.

Vamos a tomar el que tiene hipotenusa igual a 38, un cateto que mide h, que es la altura buscada y el ángulo agudo igual a 30º.

Con ayuda de las razones trigonométricas del ángulo agudo 30º determinamos el valor de h:

sen 30º = cateto opuesto a 30º / hipotenusa = h / 38

h = 38 x sen 30º = 19

Por lo tanto:

A = (1/2) x 45.8 x 19 = 435.1 unidades arbitrarias de área.

Pudimos haber escogido otro de los lados como base, por ejemplo el lado 38, en tal caso, la altura h es diferente, ya que se forma otro triángulo rectángulo, pero el resultado del área es el mismo. Queda como ejercicio para el lector comprobarlo.

– Ejercicio 3

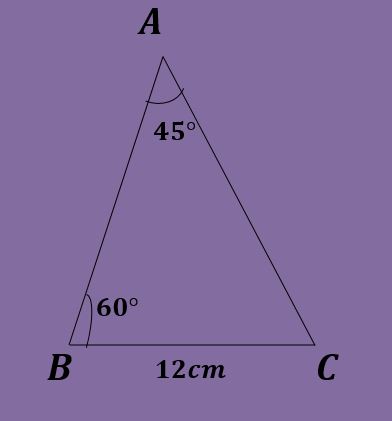
Dado un triángulo ABC tal que A=45º, B=60º y a=12 cm, calcule los demás datos del triángulo.

Solución

Utilizando que la suma de los ángulos internos de un triángulo es igual a 180º se tiene que:

C = 180º-45º-60º = 75º.

Ya son conocidos los tres ángulos. A continuación se procede a utilizar la ley de los senos para calcular los dos lados que faltan.

Las ecuaciones que se plantean son 12/ sin(45º) = b / sin(60º)  = c / sin(75º).

De la primera igualdad se puede despejar “b” y obtener que:

b = 12*sin(60º)/sin(45º) = 6√6 ≈ 14.696cm.

También se puede despejar “c” y obtener que:

c = 12*sin(75º)/sin(45º) = 6(1+√3) ≈ 16.392cm.

– Ejercicio 4

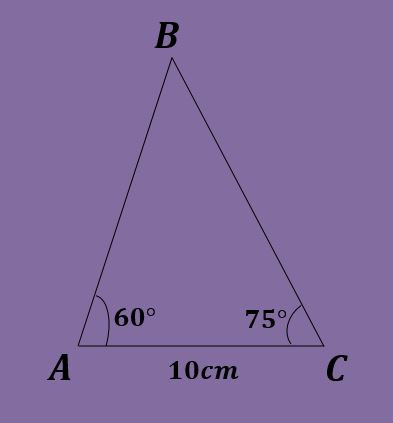
Dado el triángulo ABC tal que A=60º, C=75º y b=10cm, calcule los demás datos del triángulo.

Solución

Al igual que en el ejercicio anterior se tiene que B = 180º-60º-75º = 45º. Además, utilizando la ley de los senos se tiene que a/ sin(60º) = 10 / sin(45º)  = c / sin(75º), de donde se obtiene que a = 10*sin(60º)/sin(45º) = 5√6 ≈ 12.247 cm y c = 10*sin(75º)/sin(45º) = 5(1+√3) ≈ 13.660 cm.

– Ejercicio 5

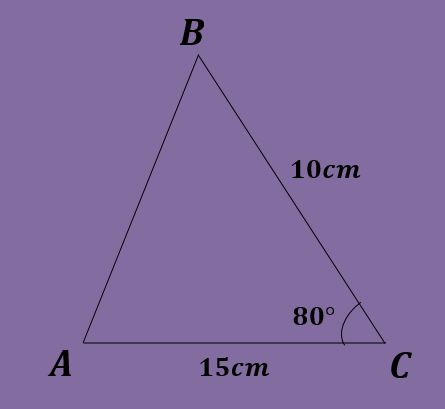
Dado el triángulo ABC tal que a=10cm, b=15cm y C=80º, calcule los demás datos del triángulo.

Solución

En este ejercicio solo es conocido un ángulo, por lo tanto no se puede comenzar como se hizo en los dos ejercicios anteriores. Además, no se puede aplicar la ley de los senos porque ninguna ecuación podría resolverse.

Por lo tanto, se procede a aplicar la ley de los cosenos. Se tiene entonces que:

c² = 10²+15² – 2(10)(15)cos(80º) = 325 – 300*0.173 ≈ 272.905 cm,

De modo que c ≈ 16.51 cm. Ahora, conociendo ya los 3 lados, se utiliza la ley de los senos y se obtiene que:

10 / sin(A) = 15 / sin(B) = 16.51cm /sin(80º).

De aquí, al despejar B resulta sin(B) = 15*sin(80º)/ 16.51 ≈ 0.894, lo que implica que B ≈ 63.38º.

Ahora, se puede obtener que A = 180º – 80º – 63.38º ≈ 36.62º.

– Ejercicio 6

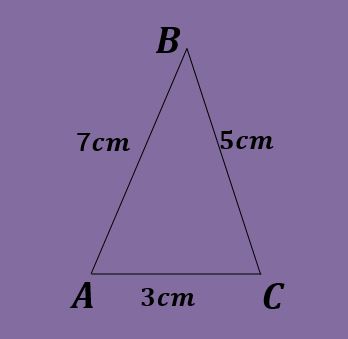
Los lados de un triángulo oblicuángulo son a=5cm, b=3cm y c=7cm. Calcule los ángulos del triángulo.

Solución

Nuevamente, no se puede aplicar la ley de los senos directamente, puesto que ninguna ecuación serviría para obtener el valor de los ángulos.

Utilizando la ley del coseno se tiene que c² = a² + b² – 2ab cos(C), de donde al despejar se tiene que cos (C) = (a² + b² – c²)/2ab = (5²+3²-7²)/2*5*3 = -15/30 = -1/2 y por lo tanto C=120º.

Ahora sí se puede aplicar la ley de los senos y así obtener 5/sin(A) = 3/sin(B) = 7/sin(120º), de donde se puede despejar B y obtener que sin(B) = 3*sin(120º)/7 = 0.371, de modo que B=21.79º.

Finalmente se calcula el último ángulo usando que A= 180º-120º-21.79º = 38.21º.

Referencias

1. Clemens, S. Geometría con Aplicaciones. Addison Wesley.
2. Ibáñez, P. 2010. Matemáticas III. Cengage Learning.
3. Jiménez, R. Matemáticas II: Geometría y Trigonometría. 2da. Edición. Pearson.
4. Matemáticas Para Ti. Triángulo obtusángulo. Recuperado de: matematicasparaticharito.wordpress.com.
5. Stewart, J. 2007. Precálculo. 5ta. Edición. Cengage Learning.