Ley de Beer-Lambert: aplicaciones y ejercicios resueltos
La ley de Beer-Lambert (Beer-Bouguer) es aquella que relaciona la absorción de la radiación electromagnética de una o varias especies químicas, con su concentración y la distancia que recorre la luz en las interacciones partícula-fotón. Esta ley reúne dos leyes en una sola.
La ley de Bouguer (aunque el reconocimiento ha recaído más sobre Heinrich Lambert), establece que una muestra absorberá mayor radiación cuando las dimensiones del medio absorbente o material sean mayores; específicamente, su grosor, que viene a ser la distancia l que recorre la luz al entrar y salir.
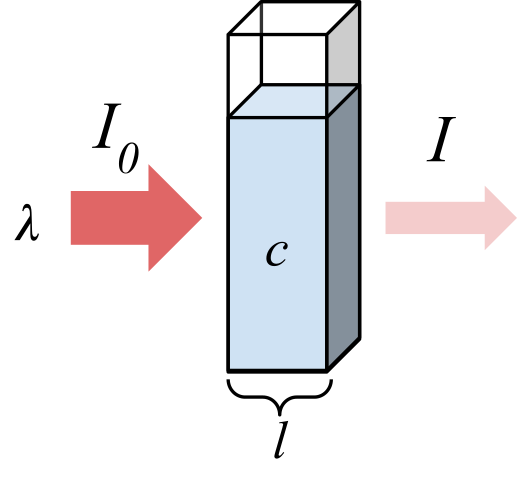
En la imagen superior se muestra la absorción de una radiación monocromática; es decir, conformada por una sola longitud de onda, λ. El medio absorbente está dentro de una celda óptica, cuyo grosor es l, y contiene especies químicas con una concentración c.
El haz de luz tiene una intensidad inicial y final, designada con los símbolos I0 y I, respectivamente. Notese que después de interaccionar con el medio absorbente, I es menor que I0, lo cual demuestra que hubo absorción de radiación. Mientras mayor sean c y l, más pequeña será I respecto a I0; es decir, habrá más absorción y menos transmitancia.
Índice del artículo
La imagen superior engloba a la perfección esta ley. La absorción de radiación en una muestra aumenta o disminuye exponencialmente en función de c o l. Para dejar entendido por completo y de manera sencilla la ley, es necesario bordear sus aspectos matemáticos.
Como recién se mencionó, I0 y I son las intensidades del haz de luz monocromática antes y después de la luz, respectivamente. Algunos textos prefieren utilizar los símbolos P0 y P, los cuales aluden a la energía de la radiación y no a su intensidad. Aquí, se continuará la explicación empleando las intensidades.
Para linealizar la ecuación de esta ley, debe aplicarse el logaritmo, generalmente el de base 10:
Log(I0/I)= εlc
El término (I0/I) indica cuánto disminuye la intensidad de la radiación producto de la absorción. La ley de Lambert considera solo a l (εl), mientras que la de Beer ignora a l, pero coloca a c en su lugar (εc). La ecuación superior es la unión de ambas leyes, y por lo tanto es la expresión matemática general para la ley de Beer-Lambert.
La absorbancia viene definida por el término Log(I0/I). Así, la ecuación se expresa como sigue:
A= εlc
Donde ε es el coeficiente de extinción o absortividad molar, la cual es una constante a una determinada longitud de onda.
Notese que si el grosor del medio absorbente se mantiene constante, al igual que ε, la absorbancia A dependerá únicamente de la concentración c, de las especies absorbentes. Además, se trata de una ecuación lineal, y=mx, donde y es A, y x es c.
A medida que aumenta la absorbancia, disminuye la transmitancia; esta es, cuánta radiación logra ser transmitida después de la absorción. Son por tanto inversos. Si I0/I indica el grado de absorción, I/I0 es igual a la transmitancia. Sabiendo esto:
I/I0 = T
(I0/I) = 1/T
Log(I0/I) = Log(1/T)
Pero, Log(I0/I) también es igual a la absorbancia. Así que la relación entre A y T es:
A= Log(1/T)
Y aplicando las propiedades de los logaritmos y sabiendo que Log1 es igual a 0:
A= -LogT
Usualmente las transmitancias se expresan en porcentajes:
%T= I/I0∙100
Como se dijo anteriormente, las ecuaciones corresponden a una función lineal; por lo tanto, se espera que al graficarlas den una recta.
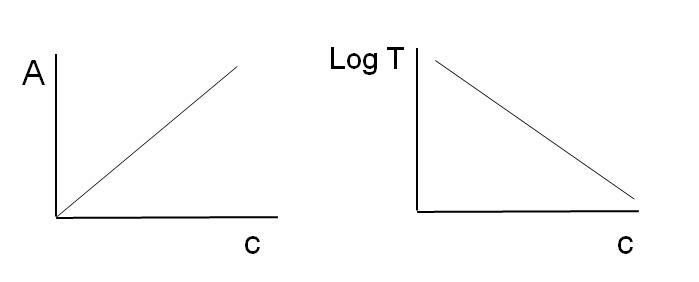
Notese que a la izquierda de la imagen de arriba se tiene la recta obtenida al graficar A contra c, y a la derecha la recta correspondiente a la gráfica de LogT contra c. Una tiene pendiente positiva, y la otra negativa; mientras mayor sea la absorbancia, menor es la transmitancia.
Gracias a esta linealidad se puede determinar la concentración de las especies químicas absorbentes (cromóforos) si se conoce cuánta radiación absorben (A), o cuánta radiación logra transmitirse (LogT). Cuando no se observa dicha linealidad, se dice que está ante una desviación, positiva o negativa, de la ley de Beer-Lambert.
En términos generales, se mencionan a continuación algunas de las aplicaciones más importantes de esta ley:
-Si una especie química presenta color, es candidato ejemplar para ser analizada por técnicas colorimétricas. Estas se fundamentan en la ley de Beer-Lambert, y permite determinar la concentración de los analitos en función de las absorbancias obtenidas con un espectrofotómetro.
-Permite construir las curvas de calibración, con las cuales tomando en cuenta el efecto matriz de la muestra, se determina la concentración de la especie de interés.
-Se usa ampliamente para analizar proteínas, ya que varios aminoácidos presentan absorciones importantes en la región ultravioleta del espectro electromagnético.
-Las reacciones químicas o fenómenos moleculares que impliquen un cambio en la coloración, pueden analizarse mediante los valores de absorbancias, a una o más longitudes de onda.
-Haciendo uso de análisis multivariante, puede analizarse mezclas complejas de cromóforos. De esta manera se puede determinar la concentración de todos los analitos, y además, clasificar las mezclas y diferenciarlas unas de otras; por ejemplo, descartar si dos minerales idénticos proceden de un mismo continente o país en específico.
¿Cuál es la absorbancia de una disolución que presenta una transmitancia del 30% a una longitud de onda de 640 nm?
Para resolverlo, basta con acudir a las definiciones de absorbancia y transmitancia.
%T= 30
T= (30/100)= 0,3
Y sabiendo que A=-LogT, el cálculo es directo:
A= -Log 0,3= 0,5228
Notese que carece de unidades.
Si la disolución del ejercicio anterior consiste de una especie W cuya concentración es 2,30∙10-4 M, y suponiendo que la celda tiene un grosor de 2 cm: ¿cuál debe ser su concentración para obtener una transmitancia del 8%?
Se pudiera resolver directamente con esta ecuación:
-LogT= εlc
Pero, se desconoce el valor de ε. Por lo tanto, hay que calcularlo con los datos anteriores, y se asume que permanece constante en un amplio rango de concentraciones:
ε = -LogT/lc
= (-Log 0,3)/ (2 cm x 2,3∙10-4 M)
=1136,52 M-1∙cm-1
Y ahora, sí se puede proceder al cálculo con %T=8:
c = -LogT/εl
= (-Log 0,08)/ (1136,52 M-1∙cm-1 x 2cm)
=4,82∙10-4 M
Entonces, basta con que la especie W duplique su concentración (4,82/2,3) para disminuir su porcentaje de transmitancia de 30% a 8%.
- Day, R., & Underwood, A. (1965). Química Analítica Cuantitativa. (quinta ed.). PEARSON Prentice Hall, p 469-474.
- Skoog D.A., West D.M. (1986). Análisis instrumental. (segunda ed.). Interamericana., México.
- Soderberg T. (18 de agosto de 2014). The Beer-Lambert Law. Chemistry LibreTexts. Recuperado de: chem.libretexts.org
- Clark J. (mayo de 2016). The Beer-Lambert Law. Recuperado de: chemguide.co.uk
- Colorimetric Analysis: Beer’s law or Spectrophotometric Analysis. Recuperado de: chem.ucla.edu
- Dr. J.M. Fernández Álvarez. (s.f.). Química analítica: manual de problemas resueltos. [PDF]. Recuperado de: dadun.unav.edu
