Números racionales: propiedades, ejemplos y operaciones
Los números racionales son todos los números que pueden obtenerse como la división de dos números enteros. Ejemplos de números racionales son: 3/4, 8/5, -16/3 y los que aparecen en la siguiente figura. En un número racional el cociente está indicado, siendo posible efectuarlo más adelante si se requiere.
En la figura se representa un objeto cualquiera, redondo para mayor comodidad. Si queremos dividirlo en 2 partes iguales, como en la derecha, nos quedan dos mitades y cada una vale 1/2.
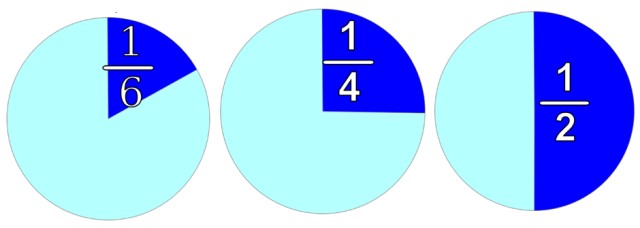
Al dividirlo en 4 partes iguales, obtendremos 4 pedazos y cada uno vale 1/4, como en la imagen del centro. Y si hay que repartirlo en 6 partes iguales, pues cada parte valdría 1/6, la cual vemos en la imagen de la izquierda.
Por supuesto, también podríamos dividirlo en dos partes no iguales, por ejemplo podríamos quedarnos con 3/4 partes y guardar 1/4 parte. Otras divisiones también son posibles, como por ejemplo 4/6 partes y 2/6 partes. Lo importante es que la suma de todas las partes resulte 1.
De esta manera, es evidente que con los números racionales se pueden dividir, contar y repartir cosas como alimentos, dinero, terrenos y toda clase de objetos en fracciones. Y así se amplía la cantidad de operaciones que se pueden hacer con los números.
Los números racionales pueden expresarse también en forma decimal, como puede verse en los siguientes ejemplos:
1/2 = 0,5
1/3 = 0,3333…..
3/4 = 0,75
1/7 = 0,142857142857142857………
Más adelante indicamos como pasar de una forma a otra con ejemplos.
Índice del artículo
- 1 Propiedades de los números racionales
- 2 Ejemplos de números racionales
- 3 Operaciones con números racionales
- 4 Referencias
Los números racionales, cuyo conjunto denotaremos con la letra Q, tienen las siguientes propiedades:
-Q incluye a los números naturales N y a los números enteros Z.
Tomando en cuenta que cualquier número a se puede expresar como el cociente entre sí mismo y el 1, es fácil ver que entre los números racionales también hay naturales y los enteros.
Así, el número natural 3 se puede escribir como fracción, y también -5:
3 = 3/1
-5= -5/1 = 5/-1 = -(5/1)
De esta forma Q es un conjunto numérico que abarca una mayor cantidad de números, algo muy necesario, puesto los números “redondos” no son suficientes para describir todas las operaciones posibles de hacer.
-Los números racionales se pueden sumar, restar, multiplicar y dividir, siendo el resultado de la operación un número racional: 1/2 + 1/5 = 7/10; 1/2 – 1/5= 3/10; (1/2)x(1/5) = 1/10; (1/2)÷(1/5) = 5/2.
-Entre cada pareja de números racionales, siempre puede hallarse otro número racional. De hecho entre dos números racionales hay infinitos racionales.
Por ejemplo, entre los racionales 1/4 y 1/2 están los racionales 3/10, 7/20, 2/5 (y muchos más), lo cual se puede verificar expresándolos como decimales.
-Cualquier número racional se puede expresar como: i) un número entero o ii) un decimal limitado (estricto) o periódico: 4/2 = 2; 1/4 = 0,25; 1/6 = 0,16666666……
-Un mismo número puede ser representado por infinitas fracciones equivalentes y todas ellas pertenecen a Q. Veamos este grupo:

Todas representan al decimal 0.428571…
-De entre todas las fracciones equivalentes que representan a un mismo número, la fracción irreducible, la más sencilla de todas, es el representante canónico de dicho número. El representante canónico del ejemplo anterior es 3/7.

-Fracciones propias, aquellas en las cuales el numerador es menor que el denominador:

-Fracciones impropias, cuyo numerador es mayor que el denominador:

-Números naturales y números enteros:

-Fracciones equivalentes:


Cuando se divide el numerador entre el denominador se encuentra la forma decimal del número racional. Por ejemplo:
2/5 = 0.4
3/8 = 0.375
1/9 = 0.11111…
6/11 = 0.545454…
En los dos primeros ejemplos, la cantidad de decimales está limitada. Esto significa que cuando se hace la división finalmente se obtiene un resto 0.
En cambio en los dos siguientes, el número de decimales es infinito y por eso se colocan los puntos suspensivos. En este último caso hay un patrón en los decimales. En el caso de la fracción 1/9 la cifra 1 se repite indefinidamente, mientras que en 6/11 es el 54.
Cuando esto sucede se dice que el decimal es periódico y se denota mediante acento circunflejo así:


Transformar un decimal a fracción
Si se trata de un decimal limitado, simplemente se elimina la coma y el denominador pasa a ser la unidad seguida de tantos ceros como cifras tenga el decimal. Por ejemplo, para transformar el decimal 1.26 en fracción se escribe así:
1.26 = 126/100
Luego se simplifica la fracción resultante al máximo:
126/100 = 63/50
Si el decimal es ilimitado primero se identifica el período. Después se siguen estos pasos para hallar la fracción resultante:
-El numerador es la resta entre el número (sin coma ni acento circunflejo) y la parte que no lleva el acento circunflejo.
-El denominador es un entero con tantos 9 como cifras hay bajo el circunflejo, y tantos 0 como cifras de la parte decimal hay que no se encuentran bajo el circunflejo.
Sigamos este procedimiento para transformar el número decimal 0,428428428… en fracción.
-Primero se identifica el período, el cual es la secuencia que se repite: 428.

-Luego se hace la operación de restar el número sin coma ni acento: 0428 de la parte que no tiene circunflejo, la cual es 0. Queda así 428 – 0 = 428.
-Se construye el denominador, sabiendo que bajo el circunflejo hay 3 cifras y todas están bajo el circunflejo. Por lo tanto el denominador es 999.
-Finalmente se forma la fracción y se simplifica de ser posible:
0.428= 428/999
No es posible simplificar más.
Fracciones con igual denominador
Cuando las fracciones tienen el mismo denominador, sumarlas y/o restarlas es muy fácil, porque simplemente se suman algebraicamente los numeradores, dejando como denominador del resultado al mismo de los sumandos. Finalmente de ser posible, se simplifica.
Ejemplo
Efectuar la siguiente suma algebraica y simplificar el resultado:

La fracción resultante ya es irreducible.
Fracciones con distinto denominador
En este caso, los sumandos se sustituyen por fracciones equivalentes con igual denominador y luego se sigue el procedimiento ya descrito.
Ejemplo
Sumar algebraicamente los siguientes números racionales simplificando el resultado:

Los pasos son:
-Determinar el mínimo común múltiplo (mcm) de los denominadores 5, 8 y 3:
mcm (5,8,3) = 120
Este será el denominador de la fracción resultante sin simplificar.
-Para cada fracción: dividir el mcm entre el denominador y multiplicar por el numerador. El resultado de esta operación se coloca, con su respectivo signo, en el numerador de la fracción. De esta forma se obtiene una fracción equivalente a la original, pero con el mcm como denominador.
Por ejemplo, para la primera fracción, el numerador se construye así: (120/5) x 4 = 96 y se obtiene:

Se procede del mismo modo para las restantes fracciones:



Por último se sustituyen las fracciones equivalentes sin olvidar su signo y se efectúa la suma algebraica de los numeradores:
(4/5) + (14/8) – (11/3) + 2 = (96/120) + (210/120) – (440/120) + (240/120) =
= (96+210-440+24) / 120 = -110 / 120 = -11/12
La multiplicación y la división se hacen siguiendo las reglas mostradas a continuación:
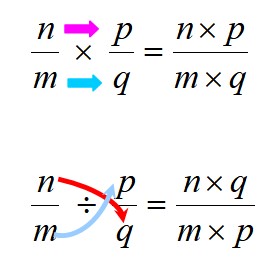
En todo caso es importante recordar que la multiplicación es conmutativa, lo que significa que el orden de los factores no altera el producto. Esto no ocurre con la división, por lo que se debe cuidar de respetar el orden entre dividendo y divisor.
Ejemplo 1
Efectuar las siguientes operaciones y simplificar el resultado:
a) (5/3) x (8/15)
b) (-4/5) ÷ (2/9)
Respuesta a
(5/3) x (8/15) = (5 x 8) / (3 x 15) = 15 / 120 = 1/8
Respuesta b
(-4/5) ÷ (2/9) = (-4 x 9) / (5 x 2) = -36 / 10 = -18/5
Ejemplo 2
Luisa tenía 45 $. Gastó una décima parte comprando un libro y 2/5 partes de lo que le quedó en una camiseta. ¿Cuánto dinero le queda a Luisa? Exprese el resultado en fracción irreducible.
Solución
El libro costó (1/10) x 45 $ = 0.1 x 45 $ = 4.5 $
Por lo tanto Luisa se quedó con:
45 – 4.5 $ = 40.5 $
Con ese dinero Luisa fue a la tienda de ropa y compró la camiseta, cuyo precio es:
(2/5) x 40.5 $ = 16.2 $
Ahora Luisa tiene en la cartera:
40.5 – 16.2 $ = 24.3$
Para expresarlo en fracción se escribe así:
24.3 = 243 / 10
Que es irreducible.
- Baldor, A. 1986. Aritmética. Ediciones y Distribuciones Códice.
- Carena, M. 2019. Manual de Matemática. Universidad Nacional del Litoral.
- Figuera, J. 2000. Matemática 8. Ediciones Co-Bo.
- Jiménez, R. 2008. Álgebra. Prentice Hall.
- Los números racionales. Recuperado de: cimanet.uoc.edu.
- Números racionales. Recuperado de: webdelprofesor.ula.ve.
