Movimiento relativo: en una dimensión, en dos dimensiones, ejercicios

El movimiento relativo de una partícula o de un objeto es el que se observa respecto a un punto de referencia particular que ha escogido el observador, el cual puede estar fijo o en movimiento. La velocidad siempre se refiere a algún sistema coordenado usado para describirlo.

Por ejemplo, el copiloto de un auto en movimiento y que viaja cómodamente dormido en su asiento está en reposo respecto al conductor, pero no lo está para un observador parado en la acera que ve pasar el coche.

Entonces el movimiento siempre es relativo, pero sucede que por lo general el sistema de coordenadas o de referencia se escoge teniendo su origen en la Tierra o el suelo, un lugar considerado estacionario. De esta forma la preocupación se centra en describir el movimiento del objeto bajo estudio.

¿Es posible describir la velocidad del copiloto dormido respecto a un pasajero que viaja en otro coche? La respuesta es sí. Hay libertad para escoger el valor de (x_o, y_o, z_o): el origen del sistema referencia. La selección es arbitraria y depende de la preferencia del observador, así como de la facilidad que brinde para la resolución del problema.

Índice del artículo

• 1 Movimiento relativo en una dimensión
  • 1.1 -Ejemplo resuelto 1
• 2 Movimiento relativo en dos y tres dimensiones
  • 2.1 -Ejercicio resuelto 2 
  • 2.2 -Ejercicio resuelto 3
• 3 Referencias

Movimiento relativo en una dimensión

Cuando el movimiento transcurre a lo largo de una línea recta, los móviles tienen velocidades en el mismo sentido o en sentido contrario, ambos vistos por un observador parado en Tierra (T). ¿Se mueve el observador respecto a los móviles? Sí, con la misma velocidad que ellos llevan, pero en sentido contrario.

¿Cómo se mueve un móvil respecto del otro? Para averiguarlo se suman las velocidades vectorialmente.

-Ejemplo resuelto 1

En referencia a la figura mostrada, indique la velocidad relativa del automóvil 1 respecto al automóvil 2 en cada situación.

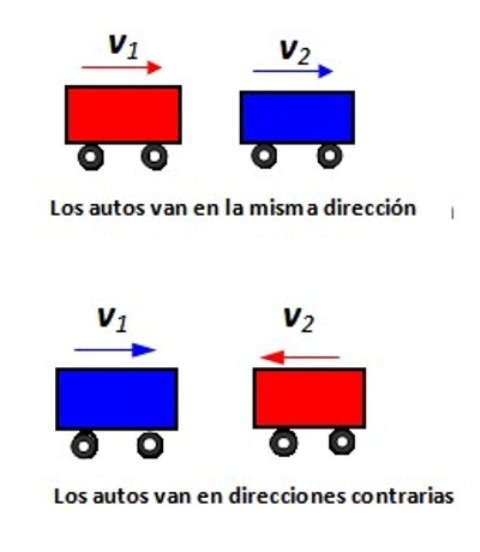
Solución

Asignaremos signo positivo a las velocidades hacia la derecha, y signo negativo a la izquierda. Si un móvil va hacia la derecha a 80 km/h, un pasajero en este móvil ve al observador en Tierra moverse a – 80 km/h.

Supongamos que todo sucede a lo largo del eje x. En la siguiente figura el automóvil rojo se mueve a +100 km/h (visto desde T) y se dispone a rebasar al automóvil azul que viaja a +80 km/h (visto también desde T). ¿Con qué velocidad ve acercarse al auto rojo un pasajero en el auto azul?

Las etiquetas son: v_1/2 velocidad del auto 1 respecto al 2, v_1/T velocidad del auto respecto a T, v_T/2 velocidad de T respecto a 2. Sumando vectorialmente:

v_1/2 = v_1/T + v_T/2 = (+100 km/h – 80 km/h) x= 20 km/h x

Podemos prescindir de la notación vectorial. Observe los subíndices: multiplicando los dos de la derecha debe obtener el de la izquierda.

¿Y cuando van en sentido contrario? Ahora v_1/T = + 80 km/h y v_2/T = -100 km/h, por lo tanto v_T/2 = + 100 km/h. El pasajero del auto azul verá al auto rojo acercarse a:

v_{1/2 =} v_1/T + v_T/2 = +80 km/h +100 km/h = 180 km/h

Movimiento relativo en dos y tres dimensiones

En el siguiente esquema, r es la posición del avión vista desde el sistema xyz, r’ es la posición desde el sistema x’y’z’ y R es la posición del sistema con prima respecto al sistema sin prima. Los tres vectores forman un  triángulo en el cual R + r’ = r, por lo tanto r’ = r – R.

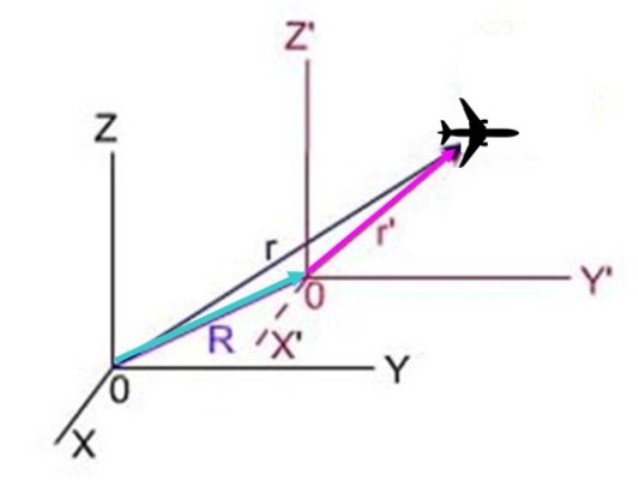
Dado que la derivada con respecto al tiempo de la posición es justamente la velocidad, resulta:

v’ = v – u

En esta ecuación v’ es la velocidad del avión con respecto al sistema x’y’z’, v es la velocidad respecto al sistema xyz yu es la velocidad constante del sistema primo respecto al sistema sin primas.

-Ejercicio resuelto 2 

Un avión va en dirección norte con velocidad respecto al aire de 240 km/h. De repente empieza a soplar viento de oeste a este a velocidad de 120 km/ según la tierra.

Encuentre: a) La velocidad del avión respecto a tierra, b) La desviación que experimenta el piloto c) La corrección que debe hacer el piloto para poder apuntar directamente al norte y la nueva velocidad respecto a tierra, una vez realizada la corrección.

Solución

a) Se tienen los elementos siguientes: avión (A), tierra (T) y viento (V).

En el sistema de coordenadas en que el norte es la dirección + y  y la dirección oeste-este es +x se tienen las velocidades dadas y su respectiva etiqueta (subíndices):

v_A/V = 240 km/h (+y); v_V/T = 120 km/h (+x) ; v _A/T = ?

La suma vectorial adecuada es:

v_A/T = v_A/V + v_V/T = 240 km/h (+y) + 120 km/h (+x)

La magnitud de este vector es: v _A/T = (240 ²+ 120²)^1/2 km/h= 268.3 km/h

b) θ = arctg (v _A/V / v _V/T) = arctg (240 /120) = 63.4º al Norte del Este o 26.6º Noreste.

c) Para seguir al norte con este viento, deberá apuntar la proa del avión hacia el noroeste, de manera que el viento lo empuje directamente hacia el norte. En tal caso la velocidad del avión vista desde tierra será en la dirección +y, mientras que la velocidad del avión respecto al viento será de a noroeste (no tiene por qué ser necesariamente 26.6º).

Por teorema de Pitágoras:

v _A/T = (240 ²– 120²)^1/2 km/h= 207.8 km/h

α = arctg (v _V/T / v _A/T ) = arctg (120 / 207.8 ) = 30º Noroeste

-Ejercicio resuelto 3

Una persona demora 2 minutos en bajar caminando por una escalera mecánica inmóvil. Si la escalera funciona, la persona tarda 1 minuto en bajar estando quieta. ¿Cuánto tarda la persona en bajar caminando y con la escalera funcionando?

Solución

Hay tres elementos a considerar: la persona (P), la escalera (E) y el suelo (S), cuyas velocidades relativas son:

v_P/E : velocidad de la persona respecto a la escalera; v_E/S: velocidad de la escalera respecto al suelo; v_P/S: velocidad de la persona respecto al suelo.

Según es vista desde el suelo por un observador fijo, la persona que baja la escalera (E) tiene una velocidad  v _P/S dada por:

v_P/S = v_P/E + v_E/S

El sentido positivo es bajando la escalera. Sea t  el tiempo que tarda en bajar caminando y L la distancia. La magnitud de la velocidad de la persona v _P/S es:

v_P/S = L / t

t₁ es el tiempo que tarda en bajar caminando con la escalera detenida: v _P/E = L / t₁

Y t₂ el que le toma bajar quieta en la escalera en movimiento: v _E/S = L / t₂

Combinando las expresiones:

L / t = L / t₁ + L / t₂

Sustituyendo valores numéricos y despejando t:

1 / t =1 / t₁ + 1 / t₂ = 1/2 + 1/1 =1.5

Entonces t = 1 /1.5 minutos = 40 segundos.

Referencias

1. Bauer, W. 2011. Física para Ingeniería y Ciencias. Volumen 1. Mc Graw Hill. 84-88.
2. Figueroa, D. Serie Física para Ciencias e Ingeniería. Volumen 3ra. Edición. Cinemática. 199-232.
3. Giancoli, D.  2006. Physics: Principles with Applications. 6^th. Ed. Prentice Hall. 62-64.
4. Relative Motion. Recuperado de: courses.lumenlearning.com
5. Wilson, J. 2011. Física 10. Pearson Educación. 166-168.