Funciones vectoriales: qué son, ejemplos y ejercicios resueltos
¿Qué son las funciones vectoriales?
Una función vectorial de un parámetro t, es una función cuyo dominio son los valores reales de t, mientras que el recorrido está formado por vectores de la forma r (t). Tal función se puede expresar como:
r (t) = f(t) i + g(t) j + h(t) k
Donde i, j y k son los vectores unitarios en las tres direcciones principales del espacio, y las funciones f, g y h son funciones reales de la variable t. La notación hace uso de las negritas, para distinguir las magnitudes vectoriales.
Otra forma de denotar una función vectorial es mediante corchetes:
r (t) =
Las funciones vectoriales pueden utilizarse para estudiar curvas en el plano y en el espacio, como la trayectoria que sigue un objeto en movimiento. Un ejemplo es la parábola descrita por una pelota proyectada con velocidad inicial, bajo la gravedad.
Si se quiere conocer la posición de la pelota a cada instante de tiempo t, se puede definir la función vectorial con dos componentes, una horizontal y otra vertical:
r (t) = x(t) i + y(t) j
Tanto x(t) como y(t) son funciones del tiempo t. Así, al unirse los puntos extremos de cada uno de los vectores r(t) posibles, forman la parábola descrita por la pelota en el plano xy.
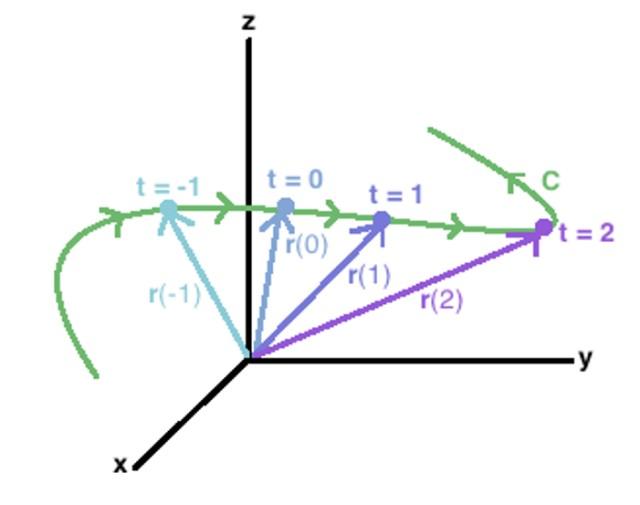
El concepto se extiende fácilmente a una curva C en el espacio, como la que se muestra en la figura de arriba. En ella aparecen los vectores r (-1), r (0), r (1) y r (2), cuyos extremos trazan la curva C, dibujada en color verde.
Límites, derivadas e integrales de las funciones vectoriales
Las herramientas de cálculo que se aplican a las funciones reales de variable real, se pueden aplicar asimismo a las funciones vectoriales.
Límite de una función vectorial
El límite de la función vectorial r (t) = f(t) i + g(t) j + h(t) k, cuando t → a, se define como:
Suponiendo que existen los límites respectivos de f(t), g(t) y h(t), cuando t → a.
Derivada de una función vectorial
La definición de derivada de una función vectorial r (t) = f(t) i + g(t) j + h(t) k es análoga a la de la derivada de una función real de variable real. Llamando r´(t) a dicha derivada, se tiene:
La derivada existe siempre que el límite anterior exista, y de ser así, la función r(t) es diferenciable en t.
Integral de una función vectorial
Sea r (t) = f(t) i + g(t) j + h(t) k una función vectorial, tal que las funciones f, g y h son integrables en t.
Entonces:
Con:
C = c1 i + c2 j
Lo que significa que la constante de integración es también un vector, pero constante.
Ejemplos de función vectorial
Ejemplo 1
Se tiene la función vectorial dada por r (t)=3sec ti + 2tan tj. Es posible evaluarla para distintos valores de t, como por ejemplo, t = π/4 y t = π, dando lugar a los vectores r (π/4) y r (π):
r (π/4) = 3sec (π/4) i + 2tan (π/4) j = 3√2 i + 2 j
r (π) = 3sec (π) i+2tan (π) j = − 3 i
Sin embargo, r (t) no existe para valores de t = ∓π/2, ∓3π/2, ∓5π/2…, ya que la función sec t = 1 /cos t no está definida, y tampoco lo está tan t = sen t / cos t.
Por lo tanto, el dominio de la función r (t) son todos los valores reales de t, excepto los de la forma:
∓ (2n+1) π/2; con n = 0, 1, 2,….
La gráfica de la función es una hipérbola:
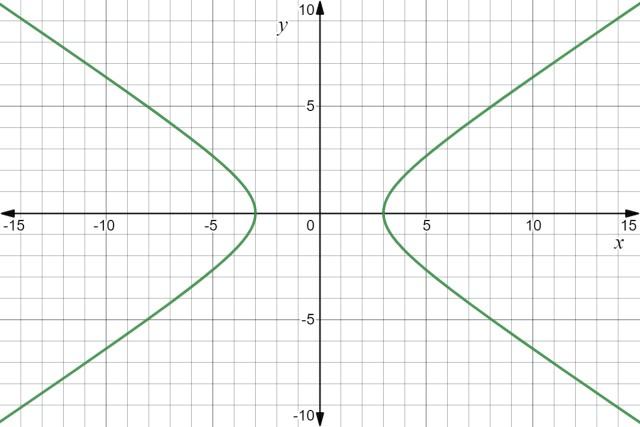
Ejemplo 2
En el lanzamiento inclinado de proyectiles, la posición del móvil es la función vectorial r (t) = x(t) i + y(t) j . Suponiendo que la resistencia del aire no interviene, y que la gravedad es la única fuerza que actúa sobre el móvil, el movimiento horizontal es rectilíneo uniforme, mientras que el vertical es uniformemente acelerado, siendo g = 9.8 m/s2 el valor de la aceleración. Dicha aceleración es vertical hacia el suelo.
En este caso, las funciones x(t) y y(t) son, respectivamente:
- x (t) = xo + vox∙t
- y (t) = yo + voy∙t – ½ gt2
Las cantidades vox y voy son las componentes de la función vectorial que describe la velocidad del móvil en todo momento:
v (t) = vx(t) i + vy(t) j
Con:
- vox = vo∙cos θ
- voy = vo∙sen θ
Siendo θ el ángulo que forma la velocidad inicial respecto a la horizontal.
Por su parte, la posición inicial del móvil es el punto de coordenadas (xo,yo), o equivalentemente, el vector de posición dado por:
ro(t) = xoi + yo j
Nótese que, en las ecuaciones mostradas, se ha asignado signo negativo a la dirección vertical hacia abajo, por eso el tercer término de la ecuación para y(t) lo lleva. También es posible asignar el origen a la posición inicial del móvil.
Velocidad instantánea del proyectil
La velocidad instantánea v (t) es la primera derivada de la posición, respecto al tiempo. Se calcula aplicando las reglas de derivación conocidas:
v(t) = r´ (t) = [x(t) i + y(t) j]´= x´(t) i + y´(t) j= vox i + (voy – gt) j
El módulo de la velocidad viene dado por:
Aceleración instantánea del proyectil
Se sabe que es g, en la dirección vertical y sentido hacia abajo. Esto se comprueba sabiendo que la aceleración es la derivada primera de la velocidad respecto al tiempo (o la derivada segunda de la posición respecto al tiempo, si se prefiere):
a(t) = v´ (t) = [vox i + (voy – gt) j]´= [vox i]´+ [(voy – gt) j]´= = – g j
Este es precisamente el resultado esperado.
Ejercicio resuelto
Dada la función vectorial r (t) = 3t i + (t−1) j, hallar r’(t) y r´´(t).
Solución
Aplicando las reglas de derivación a cada una de las componentes, se tiene:
r’(t)= = 3 i + j
Y, puesto que la derivada de una constante es 0:
r´´(t) = 0
Es decir, r´´(t) es igual al vector nulo.
Referencias
- Figueroa, D. 2005. Serie: Física para Ciencias e Ingeniería. Volumen 1. Cinemática. Editado por Douglas Figueroa (USB).
- Larson, R. Cálculo con Geometría Analítica. 2da. Edición. McGraw Hill.
- Mathonline. Vector-valued functions. Recuperado de: mathonline.wikidot.com.
- OpenStax. Calculus Volume 3. Recuperado de: openstax.org.
- Purcell, E. J. 2007. Cálculo. Pearson Educación.
