Propiedad distributiva: explicación, ejemplos y ejercicios resueltos

¿Qué es la propiedad distributiva?

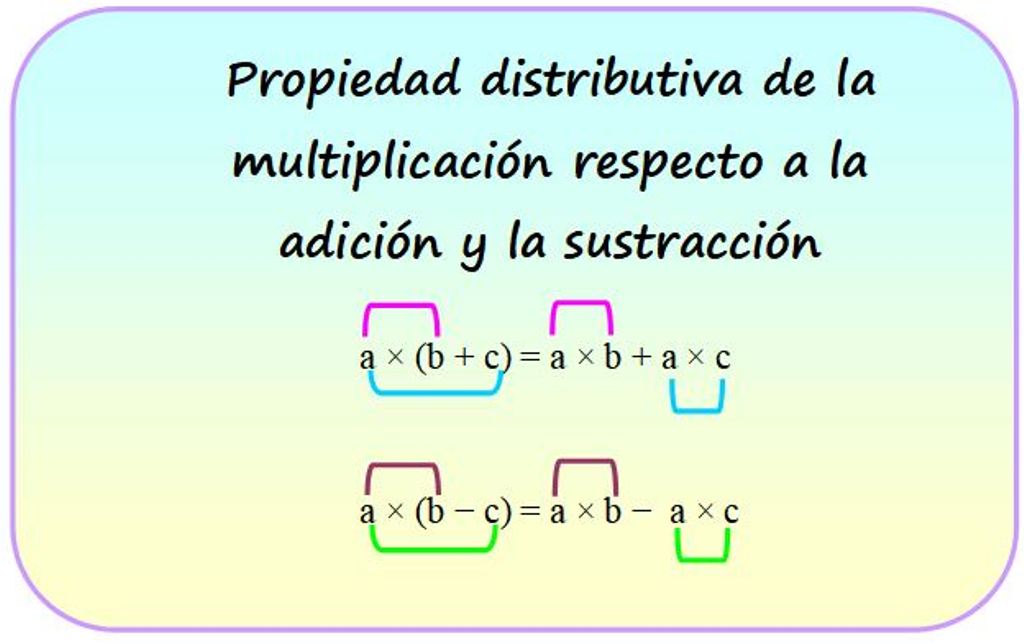
La propiedad distributiva de la multiplicación respecto a la suma o a la sustracción consiste en multiplicar un factor por la suma o resta indicada de dos o más cantidades.

Sean tres cantidades a, b y c, que pueden ser números reales, cantidades algebraicas o vectoriales, entre otras, y supóngase que se plantea resolver con ellas la siguiente operación:

a × (b + c)

En esta expresión “a” es el factor y (b + c) es la suma indicada. Hay dos maneras de encontrar la respuesta de la operación, la primera de ellas es obtener la suma (b+c) y lo que resulte, se multiplica por “a”.

Y la otra forma consiste en multiplicar “a” por cada uno de los términos b y c, y después sumar los resultados. No es raro que una misma operación se pueda hacer de varias maneras. El siguiente ejemplo demuestra que los dos procedimientos son equivalentes:

5 × (7 + 3) = 5 × 10 = 50

O bien:

5 × (7 + 3) = (5 × 7) + (5 × 3) = 35 + 15 = 50

En este último procedimiento, el 5 multiplica al 7 y luego al 3, los respectivos resultados se suman para obtener el valor final.

La propiedad distributiva también se puede aplicar a la sustracción, por ejemplo:

8 × (12 − 5) = (8 × 12) −  (8 × 5) = 96 −   40 = 56

Y en ambos casos, no importa la cantidad de términos dentro del paréntesis, ya que el factor que multiplica se distribuye a todos, como en esta otra operación:

5 × (3 − 7 + 10) = (5 × 3) −  (5 × 7) + (5 × 10)  = 15 −  35 + 50 = 30

El factor común: el inverso de la propiedad distributiva

Considérese la siguiente operación:

(7 × 2) + (7 × 6)

En cada paréntesis se observa un 7 que multiplica a otro número. Pues bien, ya que el 7 se repite en ambos paréntesis y está multiplicando, se le llama factor común, de manera que la operación se puede escribir como:

(7 × 2) + (7 × 6) = 7 × (2 + 6)

Esta operación es precisamente la inversa de la propiedad distributiva y se puede aplicar a cualquier cantidad de términos que tengan un factor común, por ejemplo:

(6 × 8) + (6 × 11) + (6 × 4) − (6 × 9)

El factor común es el 6, puesto que se repite en cada uno de los términos. Por lo tanto:

(6 × 8) + (6 × 11) + (6 × 4) − (6 × 9)= 6 × (8 + 11+ 4− 9)

Observaciones

Siempre que se piense en aplicar la propiedad distributiva es necesario observar la notación, en este sentido es importante destacar que:

• Los símbolos de cruz “×” y punto a media altura “∙” se utilizan indistintamente para denotar una multiplicación.
• Incluso si ninguno de estos símbolos está presente entre el factor y el paréntesis que contene los sumandos, se entenderá que se trata de una multiplicación. Por ejemplo, en la operación 5(4 − 9), el 5 multiplica tanto al 4 como al 9, de la misma forma que en los ejemplos anteriores:

5(4− 9) = 5∙4−5∙9 = 20 − 45 = −25

En este ejemplo también se utilizó el punto a media altura en vez de la cruz.

Otro hecho importante a tener en cuenta es la presentación de las operaciones, no es igual 7(5+1) que 7 + (5×1). En el primer caso se aplica la propiedad distributiva de la misma forma que se ha venido haciendo:

7(5+1) = 7∙5 + 7∙1 = 35+7=42

En cambio para la operación 7 + (5×1) se procede de acuerdo a la jerarquía de operaciones, la cual señala que los paréntesis deben ser eliminados en primer lugar, de esta manera:

7 + (5×1) = 7 + 5 = 12

• La multiplicación es conmutativa, por lo tanto se cumple que:

a × (b + c) = (b + c) × a

El factor que multiplica a la suma puede estar a la izquierda o a la derecha de esta y en todo caso el resultado es el mismo.

Ejemplos de aplicación

Ejemplo 1

Se puede llevar a cabo la multiplicación de un número grande por otro, a través de la propiedad distributiva, si el número grande se descompone en centenas, decenas y unidades. Por ejemplo se pide efectuar:

5×852

El número 852 se descompone en sumandos como:

852 = 800 + 50 + 2

Y la operación solicitada se escribe como:

5×852= 5×(800 + 50 + 2)

Ahora solo hay que aplicar la propiedad distributiva y obtener la suma resultante:

5×(800 + 50 + 2) = 4000 + 250 + 10 = 4260

Ejemplo 2

La propiedad distributiva facilita el cálculo de productos de sumas, productos de diferencias y productos de sumas por diferencias:

(a + b) × (c + d) = a∙c + a∙d + b∙c + b∙d

(a + b) × (c − d) = a∙c − a∙d + b∙c − b∙d

(a − b) × (c − d) = a∙c − a∙d − b∙c + b∙d

Por ejemplo, las siguientes operaciones se resuelven como se muestra:

(5 + 4) × (2 + 13) = 5∙2 + 5∙13 + 4∙2 + 4∙13 =10 + 65 + 8 +52 = 135

[(8 + (−17)] × (6 − 21) = 8∙6 − 8∙21 + (− 17)∙6 − (− 17)∙21 = 48−168−102+357 =135

(11 − 7) × (9 − 16) = 11∙9 − 11∙16 − 7∙9 + 7∙16 = 99 − 176 − 63 +112 = −28

Ejemplo 3

El mostrador de una floristería tiene cuatro jarrones con flores y en cada uno de ellos hay 9 rosas y 2 claveles. Se puede emplear la propiedad distributiva para hallar la cantidad total de flores en los cuatro jarrones, simplemente multiplicando por 4 la suma (9 + 2):

Total de flores = 4× (9 + 2) = 36 + 8 = 44 flores

La propiedad distributiva en el álgebra

Tanto la propiedad distributiva como el factor común tienen amplio uso en álgebra y cálculo, ya que permiten manipular expresiones algebraicas fácilmente, según la conveniencia.

En ocasiones es mejor desarrollar una expresión con la propiedad distributiva, mientras que en otras puede resultar más eficaz tener la expresión factorizada.

Por ejemplo, supóngase que se necesita desarrollar la expresión:

2(x+1)

A diferencia de la operación 5 × (7 + 3) = 5 × 10 = 50, los términos dentro del paréntesis no son semejantes, así que su suma no se reduce a un solo término (en cambio 7 + 3 se reduce de inmediato a 10). En tal caso, se aplica la propiedad distributiva para obtener:

2(x+1) = 2∙x + 2∙1=2x + 2

Uso de la propiedad distributiva para resolver ecuaciones

Algunas ecuaciones algebraicas se resuelven aplicando la propiedad distributiva, por ejemplo:

8(x–2) = 14

Aplicando la propiedad distributiva para desarrollar el lado izquierdo de la igualdad se tiene:

8x – 16 = 14

8x = 14 + 16 = 30

x = 30/8 = 15/4

Productos notables

La propiedad distributiva sirve para demostrar los productos notables, que se usan mucho en álgebra. Por ejemplo se puede demostrar que el producto de la suma de dos cantidades multiplicada por la diferencia de esas mismas cantidades es igual a la diferencia de sus respectivos cuadrados.

Denotando las cantidades como “a” y “b” y aplicando la propiedad se tiene:

(a + b) × (a – b) = a⋅a – a⋅b + a⋅b – b⋅b = a² – b²

Ejercicios resueltos

Ejercicio 1

Un grupo de 8 amigos se van de paseo una tarde para visitar un museo y comer una merienda. El transporte cuesta 5 €, la entrada 2€ y el refrigerio de 3€ por persona. Calcular el costo del paseo para todo el grupo.

• Solución

Cada participante tiene que gastar (5 + 2 + 3) € por persona, y como son 8, el total se calcula mediante la siguiente operación:_

8×(5 + 2 + 3) € = (8×5 + 8×2 + 8×3) € = (40 + 16 + 24) € = 80€

Ejercicio 2

La cabina de un funicular puede llevar 30 pasajeros sentados y 12 pasajeros de pie. Calcular cuántos pasajeros son transportados después de 9 viajes si cada uno lleva el máximo de personas permitido.

• Solución

El total de personas que van en un solo viaje es (30 + 12), como son 9 viajes queda:

9×(30 + 12) = 9×30 + 9×12 = 270 + 108 = 378 personas.

Referencias

1. Baldor, A. 1985. Aritmética Teórico-Práctica. Ediciones y Distribuciones Códice, Madrid.
2. Lecciones de Mates. Ejercicios resueltos de la propiedad distributiva y sacar factor común. Recuperado de: leccionesdemates.com.
3. Matemáticas Mamut. Propiedad distributiva o cómo multiplicar en partes. Recuperado de: mamutmatematicas.com.
4. Smartick. Ejemplos de propiedad distributiva. Recuperado de: smartick.es.
5. Vicen Vives. Matemáticas 4, Tema: multiplicación. Recuperado de: auladecarmela.com