Números compuestos: características, ejemplos, ejercicios
Los números compuestos son aquellos enteros que poseen más de dos divisores. Si nos fijamos bien, todos los números son al menos divisibles exactamente entre sí mismos y entre el 1. Aquellos que solamente tienen estos dos divisores se llaman primos, y los que tienen más son compuestos.
Observemos al número 2, que solamente puede dividirse entre 1 y 2. El número 3 también posee dos divisores: el 1 y el 3. Por lo tanto ambos son primos. Ahora veamos al número 12, al cual podemos dividir exactamente entre 2, 3, 4, 6 y 12. Al tener 5 divisores, el 12 es un número compuesto.
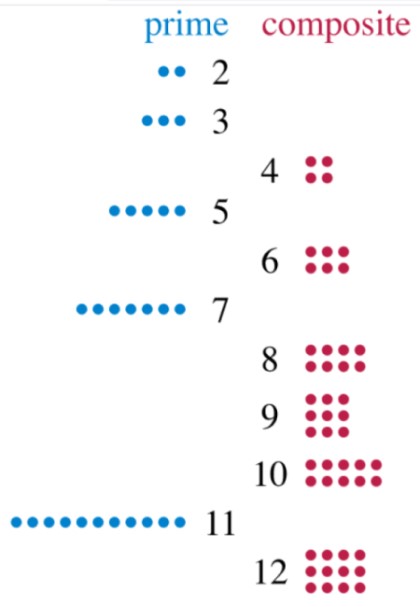
¿Y qué sucede con el número 1, ese que divide a todos los demás? Pues no es primo, porque no tiene dos divisores, y tampoco es compuesto, por lo tanto el 1 no cae dentro de ninguna de estas dos categorías. Pero hay muchísimos números más que sí lo hacen.
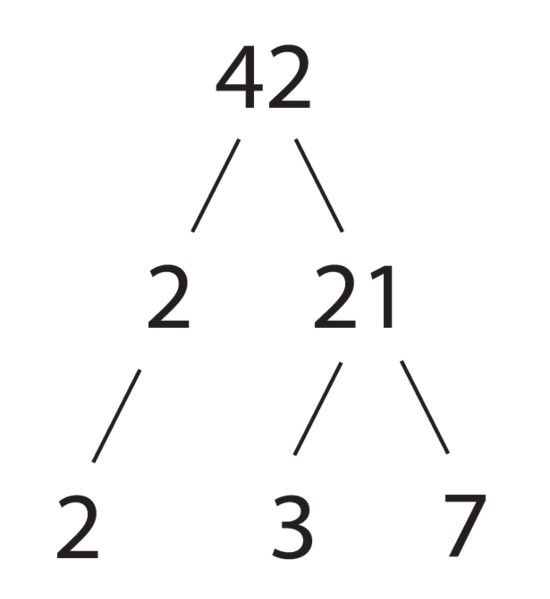
Los números compuestos pueden ser expresados como el producto de números primos, y este producto, salvo el orden de los factores, es único para cada número. Así lo asegura el teorema fundamental de la aritmética demostrado por el matemático griego Euclides (325-365 aC).
Volvamos al número 12, al que podemos expresar de varias maneras. Probemos algunas:
12 = 4 x 3 = 2 x 6 = 12 x 1 = 22 x 3 = 3 x 22 = 3 x 2 x 2 = 2 x 2 x 3 = 2 x 3 x 2
Las formas que están resaltadas en negrita son productos de números primos y lo único que cambia es el orden de los factores, el cual sabemos que no altera el producto. Las otras formas, aunque válidas para expresar el 12, no constan únicamente de primos.
Ejemplos de números compuestos
Si queremos descomponer un número compuesto en sus factores primos debemos dividirlo entre números primos de forma tal que la división sea exacta, es decir, que el residuo sea 0.
A este procedimiento se le llama descomposición en factores primos o descomposición canónica. Los factores primos pueden estar elevados a exponentes positivos.
Vamos a descomponer el número 570, notando que es par y por lo tanto divisible entre 2, que es un número primo.
Usaremos una barra para separar el número a la izquierda de los divisores a la derecha. Los respectivos cocientes se colocan debajo del número a medida que se van obteniendo. La descomposición se completa cuando la última cifra en la columna izquierda es 1:
570 │2
285 │
Al dividir entre 2 el cociente es 285 que es divisible entre 5, otro número primo, por terminar en 5.
570 │2
285 │5
57 │
El 57 es divisible entre 3, también primo, ya que la suma de sus dígitos 5 +7 = 12 es múltiplo de 3.
570 │2
285 │5
57 │3
19 │
Finalmente obtenemos 19, que es un número primo, cuyos divisores son 19 y 1:
570 │2
285 │5
57 │3
19 │19
1 │
Al obtener el 1 ya podemos expresar 570 de esta forma:
570 = 2 x 5 x 3 x 19
Y vemos que en efecto, se trata del producto de 4 números primos.
En este ejemplo comenzamos dividiendo entre 2, pero los mismos factores (en otro orden) se hubieran obtenido si se comenzaba por dividir entre 5 por ejemplo.
Criterios de divisibilidad
Para descomponer un número compuesto en sus factores primos es necesario dividirlo de manera exacta. Los criterios de divisibilidad entre números primos son reglas que permiten saber cuando un número es divisible entre otro exactamente, sin tener que tantear o probar.
–Divisibilidad entre 2
Todo número par, aquellos que terminan en 0 o una cifra par son divisibles entre 2.
–Divisibilidad entre 3
Si la suma de los dígitos de un número es múltiplo de 3, entonces el número también y por consiguiente divisible entre 3.
–Divisibilidad entre 5
Los números que terminan en 0 o en 5 son divisibles entre 5.
-Divisibilidad entre 7
Un número es divisible entre 7 si al separar la última cifra, multiplicarla por 2 y restarle el número que queda, el valor resultante es múltiplo de 7.
Esta regla parece un poco más complicada que las anteriores, pero en realidad no lo es tanto, así que veamos un ejemplo: ¿será 98 divisible entre 7?
Sigamos las instrucciones: separamos la última cifra que es 8, la multiplicamos por 2 que da 16. El número que queda al separar el 8 es 9. Restemos 16 – 9 = 7. Y como 7 es múltiplo de sí mismo, 98 es divisible entre 7.
-Divisibilidad entre 11
Si la suma de las cifras en posición par (2, 4, 6…) se resta la suma de las cifras de posición impar (1, 3, 5, 7…) y se obtiene 0 o un múltiplo de 11, el número es divisible por 11.
Los primeros múltiplos de 11 se identifican fácilmente: son 11, 22, 33, 44…99. Pero atención, 111 no lo es, en cambio 110 sí.
A modo de ejemplo veamos si 143 es múltiplo de 11.
Este número tiene 3 cifras, la única cifra par es 4 (la segunda), las dos cifras impares son 1 y 3 (primera y tercera), y su suma es 4.
Se restan ambas sumas: 4 – 4 = 0 y como se obtiene 0, resulta que143 es múltiplo de 11.
-Divisibilidad entre 13
Se debe restar el número sin el dígito de las unidades de 9 veces dicho dígito. Si la cuenta da 0 o un múltiplo de 13, el número es múltiplo de 13.
Como ejemplo verificaremos que 156 es múltiplo de 13. El dígito de las unidades es 6 y el número que queda sin él es 15. Multiplicamos 6 x 9= 54 y ahora restamos 54 – 15 = 39.
Pero 39 es 3 x 13, por lo tanto 56 es múltiplo de 13.
Números primos entre sí
Puede que dos o más números primos o compuestos, sean primos entre sí o coprimos. Esto significa que el único divisor común que tienen es el 1.
Hay dos propiedades importantes para recordar en cuanto a los coprimos:
-Dos, tres y más números consecutivos siempre son primos entre sí.
-Lo mismo puede decirse de dos, tres o más números impares consecutivos.
Por ejemplo 15, 16 y 17 son números primos entre sí y también lo son 15, 17 y 19.
Cómo saber cuántos divisores tiene un número compuesto
Un número primo tiene dos divisores, el mismo número y el 1. ¿Y cuántos divisores tiene un número compuesto? Estos pueden ser primos o compuestos.
Sea N un número compuesto expresado en términos de su descomposición canónica como sigue:
N = an . bm. cp … rk
Donde a, b, c…r son los factores primos y n, m, p… k los respectivos exponentes. Pues bien, la cantidad de divisores C que tiene N viene dada por:
C = (n +1) (m+1) (p +1 )… (k+1)
Con C = divisores primos + divisores compuestos + 1
Por ejemplo el 570, que viene expresado así:
570 = 2 x 5 x 3 x 19
Todos los factores primos están elevados a la 1, por lo tanto 570 tiene:
C = (1+1) (1+1) (1+ 1) (1 +1) = 16 divisores
De estos 10 divisores ya conocemos a: 1, 2, 3, 5, 19 y 570. Faltan 10 divisores más, que son números compuestos: 6, 10, 15, 30, 38, 57, 95, 114, 190 y 285. Se encuentran observando la descomposición en factores primos y también multiplicando entre sí combinaciones de dichos factores.
Ejercicios resueltos
– Ejercicio 1
Descomponer en factores primos los siguientes números:
a) 98
b) 143
c) 540
d) 3705
Solución a
98 │2
49 │7
7 │7
1 │
98 = 2 x 7 x 7
Solución b
143 │11
13 │13
1 │
143 = 11 x 13
Solución c
540 │5
108 │2
54 │2
27 │3
9 │3
3 │3
1 │
540 = 5 x 2 x 2 x 3 x 3 x 3= 5 x 22 x 33
Solución d
3705 │5
741 │3
247 │13
19 │19
1 │
3705 = 5 x 3 x 13 x 19
– Ejercicio 2
Averiguar si los siguientes números son primos entre sí:
6, 14, 9
Solución
-Los divisores de 6 son: 1, 2, 3, 6
-En cuanto al 14, es divisible por: 1, 2, 7, 14
-Finalmente 9 tiene como divisores: 1, 3, 9
El único divisor que tienen en común es el 1, por lo tanto son primos entre sí.
Referencias
- Baldor, A. 1986. Aritmética. Ediciones y Distribuciones Códice.
- Byju’s. Prime and composite numbers. Recuperado de: byjus.com.
- Números primos y compuestos. Recuperado de: profeyennyvivaslapresentacion.files.wordpress.com
- Smartick. Criterios de divisibilidad. Recuperado de: smartick.es.
- Wikipedia. Composite numbers. Recuperado de: en.wikipedia.org.
