Óvalo (figura geométrica): características, ejemplos, ejercicios
El óvalo simétrico se define como una curva plana y cerrada, que posee dos ejes de simetría perpendiculares -uno mayor y otro menor- y está conformada por dos arcos de circunferencia iguales dos a dos.
De esta forma se puede trazar con ayuda de un compás y algunos puntos de referencia sobre uno de los ejes de simetría. En todo caso, existen varias maneras de trazarlo, como veremos luego.

Es una curva muy familiar, pues se la reconoce como el contorno de una elipse, siendo esta un caso particular del óvalo. Pero el óvalo no es una elipse aunque en ocasiones se le parezca mucho, ya que sus propiedades y trazado difieren. Por ejemplo la elipse no se construye con compás.
Índice del artículo
El óvalo tiene aplicaciones muy variadas: arquitectura, industria, diseño gráfico, relojería y joyería son solamente algunas áreas donde se destaca su uso.
Las características más destacadas de esta importante curva son las siguientes:
-Pertenece al grupo de curvas técnicas: se traza formando arcos de circunferencia con ayuda de un compás.
-Todos sus puntos se encuentran sobre un mismo plano.
-Carece de curvas o lazos.
-Su trazado es continuo.
-La curva del óvalo debe ser suave y convexa.
-Al trazar una recta tangente al óvalo, todo él se encuentra del mismo lado de la recta.
-Un óvalo solo admite dos tangentes paralelas a lo sumo.
Existen varios métodos para construir óvalos que requieren el uso de regla, escuadra y compás. Seguidamente vamos a mencionar algunos de los más usados.
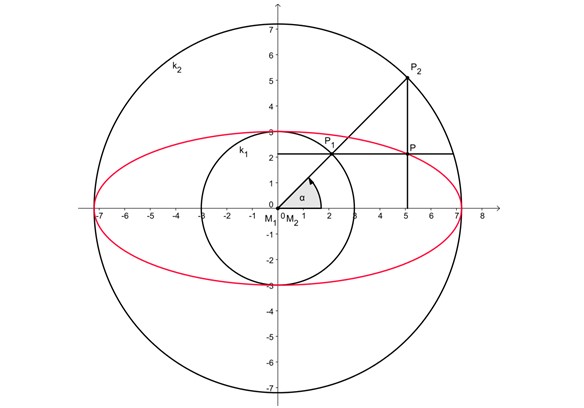
La figura 2, arriba, muestra dos circunferencias concéntricas con centro en el origen. El eje mayor del óvalo mide lo mismo que el diámetro de la circunferencia externa, mientras que el eje menor corresponde al diámetro de la circunferencia interior.
-Se traza un radio arbitrario hasta la circunferencia exterior, que corta a ambas circunferencias en los puntos P1 y P2.
-Seguidamente se proyecta el punto P2 sobre el eje horizontal.
-En forma semejante, se proyecta el punto P1 sobre el eje vertical.
-La intersección de ambas líneas de proyección es el punto P y pertenece al óvalo.
-Todos los puntos de esta sección del óvalo se pueden trazar de esta manera.
-El resto del óvalo se traza con el procedimiento análogo, llevado a cabo en cada cuadrante.
Seguidamente se examinarán otras formas de construir óvalos, dada una cierta medida inicial, que determinará su tamaño.
Trazar con ayuda de regla y compás un óvalo, conocido su eje mayor cuya longitud es 9 cm.
Solución
En la figura 3, que se muestra a continuación, aparece el óvalo resultante en color rojo. Hay que prestar especial atención a las líneas punteadas, que son las construcciones auxiliares necesarias para dibujar un óvalo cuyo eje mayor se especifica. Vamos a indicar todos los pasos necesarios para llegar al dibujo final.
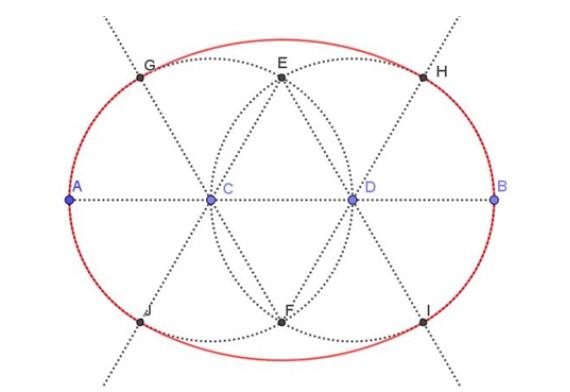
Paso 1
Trazar con una regla el segmento AB de 9 cm.
Paso 2
Trisectar el segmento AB, es decir, dividirlo en tres segmentos de igual longitud. Como el segmento original AB mide 9 cm, los segmentos AC, CD y DB deben medir 3 cm cada uno.
Paso 3
Con el compás, haciendo centro en C y apertura CA se traza una circunferencia auxiliar. Similarmente se dibuja con el compás la circunferencia auxiliar de centro D y radio DB.
Paso 4
Se marcan las intersecciones de las dos circunferencias auxiliares construidas en el paso anterior. Le llamamos puntos E y F.
Paso 5
Con la regla se trazan las siguientes semirrectas: [FC), [FD), [EC), [ED).
Paso 6
Las semirrectas del paso anterior cortan a las dos circunferencias auxiliares en los puntos G, H, I, J respectivamente.
Paso 7
Con el compás se hace centro en F y con apertura (o radio) FG se traza el arco GH. Similarmente, haciendo centro en E y con radio EI se traza el arco IJ.
Paso 8
La unión de los arcos GJ, JI, IH y HG forman un óvalo cuyo eje mayor mide 9 cm.
Paso 9
Se procede a borrar (ocultar) los puntos y trazos auxiliares.
Trazar con regla y compás un óvalo, cuyo eje menor es conocido y su medida es 6 cm.
Solución
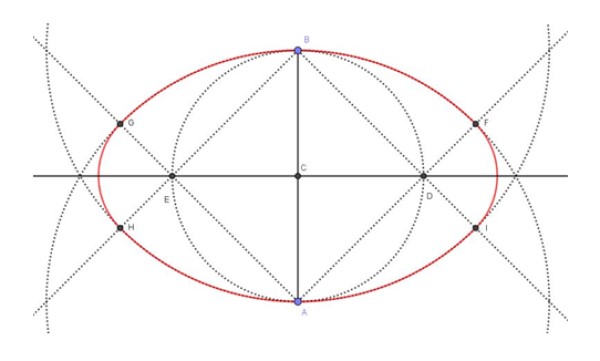
La figura de arriba (figura 4) muestra el resultado final de la construcción del óvalo (en rojo), así como las construcciones intermedias necesarias para llegar a él. Los pasos que se siguieron para construir el óvalo de eje menor 6 cm fueron los siguientes:
Paso 1
Se traza con la regla el segmento AB de 6 cm de longitud.
Paso 2
Con el compás y la regla se traza la mediatriz al segmento AB.
Paso 3
La intersección de la mediatriz con el segmento AB, da como resultado el punto medio C del segmento AB.
Paso 4
Con el compás se traza la circunferencia de centro C y radio CA.
Paso 5
La circunferencia trazada en el paso anterior intercepta a la mediatriz de AB en los puntos E y D.
Paso 6
Se trazan las semirrectas [AD), [AE), [BD) y [BE).
Paso 7
Con el compás se trazan las circunferencias de centro A y radio AB y la de centro B y radio BA.
Paso 8
Las intersecciones de las circunferencias trazadas en el paso 7, con las semirrectas construidas en el paso 6, determinan cuatro puntos, a saber: F, G, H, I.
Paso 9
Con centro en D y radio DI se traza el arco IF. De la misma forma, con centro en E y radio EG se traza el arco GH.
Paso 10
La unión de los arcos de circunferencia FG, GH, HI e IF determinan el óvalo buscado.
- Ed Plástica. Curvas técnicas: óvalos, ovoides y espirales. Recuperado de: dibujonavarres.wordpress.com.
- Mathematische Basteleien. Egg Curves and Ovals. Recuperado de: mathematische-basteleien.
- Universidad de Valencia. Cónicas y Curvas Técnicas Planas. Recobrado de: ocw.uv.es.
- Wikipedia. Óvalo. Recuperado de: es.wikipedia.org.
- Wikipedia. Oval. Recuperado de: en.wikipedia.org.
