Física

Velocidad angular: definición, fórmula, cálculo y ejercicios

La velocidad angular es una medida de la velocidad de rotación y se define como el ángulo que gira el vector de posición del objeto que rota, por unidad de tiempo. Es una magnitud que describe muy bien el movimiento de multitud de objetos que constantemente giran en todas partes: CDs, ruedas de autos, maquinarias, la Tierra y muchos más.

Un esquema del “London eye” se aprecia en la siguiente figura. En ella se representa el movimiento de un pasajero representado por el punto P, que sigue la trayectoria circular, denominada c:

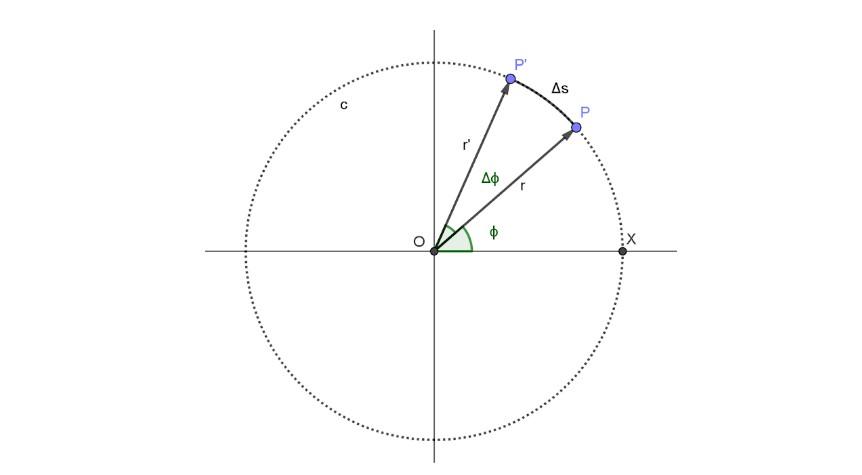
El pasajero ocupa la posición P en el instante t y la posición angular correspondiente a ese instante es ϕ.

A partir del instante t transcurre un lapso de tiempo Δt. En ese lapso la nueva posición del pasajero puntual es P’ y la posición angular se ha incrementando un ángulo Δϕ.

Índice del artículo

¿Cómo se calcula la velocidad angular ?

Para las magnitudes rotacionales se utilizan mucho las letras griegas, a fin de diferenciarlas de las magnitudes lineales. Así que inicialmente se define la velocidad angular media ωm como el ángulo recorrido en un lapso de tiempo dado.

Entonces el cociente Δϕ/Δt representará la velocidad angular media ωm entre los instantes t y t+Δt.

Si se quiere calcular la velocidad angular justo en el instante t, entonces habrá que calcular el cociente Δϕ/Δt cuando Δt ➡0:

Relación entre rapidez lineal y angular

La rapidez lineal v, es el cociente entre la distancia recorrida y el lapso de tiempo empleado en recorrerla.

En la figura de arriba, el arco recorrido es Δs. Pero ese arco es proporcional al ángulo recorrido y al radio, cumpliéndose la siguiente relación, la cual es válida siempre que Δϕ esté medido en radianes:

Δs = r・Δϕ

Si dividimos la expresión anterior entre el lapso de tiempo Δt y tomamos el límite cuando Δt ➡0, obtendremos:

v = r・ω

Movimiento de rotación uniforme

Un movimiento de rotación es uniforme si en cualquier instante observado, el ángulo recorrido es el mismo en el mismo lapso de tiempo.

Si la rotación es uniforme, entonces la velocidad angular en cualquier instante coincide con la velocidad angular media.

Además, cuando se da una vuelta completa el ángulo recorrido es 2π ( equivalente a 360º). Por eso en una rotación uniforme la velocidad angular ω se relaciona con el periodo T, mediante la siguiente fórmula:

f = 1/T

Es decir que en una rotación uniforme, la velocidad angular se relaciona con la frecuencia mediante:

ω = 2π・f

Ejercicios resueltos de velocidad angular

Ejercicio 1

Las cabinas de la gran rueda giratoria conocida como el “El ojo de Londres” se mueven lentamente. La rapidez de las cabinas es de 26 cm/s y la rueda tiene 135 m de diámetro.

Con estos datos calcule:

i) La velocidad angular de la rueda

ii) La frecuencia de rotación

iii) El tiempo que le toma a una cabina dar la vuelta completa.

Respuestas:

i) La rapidez v en m/s es:  v = 26 cm/s = 0,26 m/s.

El radio es la mitad del diametro: r= (135 m) / 2 = 67,5 m

v = r・ω   => ω = v/r = (0,26 m/s)/(67,5 m) = 0,00385 rad/s

ii) ω = 2π・f   => f = ω / 2π = (0,00385 rad/s) / ( 2π rad) = 6,13 x 10-4 vueltas/s

f = 6,13 x 10^-4 vuelta/s = 0,0368 vuelta/min = 2,21 vuelta/hora.

iii) T= 1 / f = 1 / 2,21 vuelta/hora = 0,45311 hora = 27 min 11 seg

Ejercicio 2

Una auto de juguete se mueve en una pista circular de 2m de radio. A los 0 s su posición angular es 0 rad, pero al cabo de un tiempo t su posición angular viene dada por:

φ(t) = 2・t 

Determine:

i) La velocidad angular 

ii) La rapidez lineal en cualquier instante.

Respuestas:

i) La velocidad angular es la derivada de la posición angular: ω = φ’(t) = 2.

Es decir que el auto de juguete en todo instante tiene velocidad angular constante igual a 2 rad/s.

ii) La rapidez lineal del auto es: v = r・ω = 2 m ・2 rad/s = 4 m/s = 14,4 Km/h

Ejercicio 3

El mismo auto del ejercicio anterior comienza a detenerse. Su posición angular como función del tiempo está dada por la siguiente expresión:

φ(t) = 2・t – 0,5・t2 

Determine:

i) La velocidad angular en cualquier instante

ii) La rapidez lineal en cualquier instante

iii) El tiempo que le toma detenerse a partir del instante en que comienza a desacelerar

iv) El ángulo recorrido 

v) a distancia recorrida

Respuestas:

i) La velocidad angular es la derivada de la posición angular: ω = φ’(t)

ω(t) = φ’(t) = (2・t – 0,5・t2)’ = 2 – t

ii) La rapidez lineal del auto en cualquier instante está dada por:

v(t) = r・ω(t) = 2・(2 – t) = 4 – 2 t

iii) El tiempo que le toma detenerse a partir del instante en que comienza a desacelerar, se determina sabiendo  el instante en el que la velocidad v(t) se hace cero.

v(t) =  4 – 2 t = 0  => t = 2

Es decir que se detiene 2 s después de comenzar a frenar.

iv) En el lapso de 2s comprendido desde que comienza a frenar hasta que se detiene se recorre un ángulo dado por φ(2) :

φ(2) = 2・2 – 0,5・2^2 = 4 – 2 = 2 rad = 2 x 180 /  π = 114,6 grados

v) En el lapso de 2 s comprendido desde que comienza a frenar hasta que se detiene se recorre una distancia s dada por:

s = r・φ = 2m ・2 rad = 4 m

Ejercicio 4

Las ruedas de un automóvil tienen 80 cm de diámetro. Si el automóvil se desplaza a 100 Km/h. Encuentre: i) la velocidad angular de rotación de las ruedas, ii) la frecuencia de rotación de las ruedas, iii) El número de vueltas que da la rueda en un recorrido de 1 hora.

Respuestas:

i) En primer lugar vamos a convertir la rapidez del automóvil de Km/h a m/s

v = 100 Km/h = (100 / 3.6) m/s = 27,78 m/s

La velocidad angular de rotación de las ruedas está dada por:

ω = v/r = (27,78 m/s)/(0,4 m) = 69,44 rad/s

ii) La frecuencia de rotación de las ruedas está dada por:

f = ω / 2π = (69,44 rad/s) / ( 2π rad) = 11,05 vuelta/s

La frecuencia de rotación suele expresarse en revoluciones por minuto r.p.m.

f = 11,05 vuelta/s = 11,05 vuelta/(1 / 60) min = 663,15 r.p.m

iii)  El número de vueltas que da la rueda en un recorrido de 1 hora, se calcula sabiendo que 1 hora = 60 min y que la frecuencia es el número de vueltas N dividido entre el tiempo en el que se dan esas N vueltas.

f = N / t  => N = f・ t  = 663,15 (vueltas/ min) x 60 min = 39788,7 vueltas.

Referencias

  1. Giancoli, D. Physics. Principles with Applications. 6th Edition. Prentice Hall. 106- 108.
  2. Resnick, R. (1999). Física. Volumen 1. Tercera edición en español. México. Compañía Editorial Continental S.A. de C.V. 67-69.
  3. Serway, R., Jewett, J. (2008). Física para Ciencias e Ingeniería. Volumen 1. 7ma. Edición. México. Cengage Learning Editores. 84-85.
  4. geogebra.org