¿Cuántas soluciones tiene una ecuación cuadrática?
Una ecuación cuadrática o ecuación de segundo grado, puede tener cero, una o dos soluciones reales, dependiendo de los coeficientes que aparezcan en dicha ecuación. Si se trabaja en los números complejos, entonces se puede decir que toda ecuación cuadrática tiene dos soluciones.
Para empezar una ecuación cuadrática es una ecuación de la forma ax²+bx+c=0, donde a, b y c son números reales y x es una variable.

Se dice que x1 es una solución de la ecuación cuadrática anterior si al reemplazar x por x1 se satisface la ecuación, es decir, si a(x1)²+b(x1)+c=0.
Si se tiene por ejemplo la ecuación x²-4x+4=0, entonces x1=2 es la solución, ya que (2)²-4(2)+4=4-8+4=0.
Por el contrario, si se sustituye x2=0 se obtiene (0)²-4(0)+4=4 y como 4≠0 entonces x2=0 no es solución de la ecuación cuadrática.
Soluciones de una ecuación cuadrática
El número de soluciones de una ecuación cuadrática se puede separar en dos casos que son:
1.-En los números reales
Cuando se trabaja con los números reales, las ecuaciones cuadráticas pueden tener:
-Cero soluciones: es decir, que no existe ningún número real que satisfaga la ecuación cuadrática. Por ejemplo, la ecuación dada la ecuación x²+1=0, no existe ningún número real tal que satisfaga dicha ecuación, ya que tanto x² es mayor o igual que cero y 1 es mayor estricto que cero, de modo que su suma será mayor estricta que cero.
-Una solución repetida: existe un único valor real que satisface la ecuación cuadrática. Por ejemplo, la única solución de la ecuación x²-4x+4=0 es x1=2.
-Dos soluciones distintas: existen dos valores que satisfacen la ecuación cuadrática. Por ejemplo, x²+x-2=0 tiene dos soluciones distintas que son x1=1 y x2=-2.
2.- En los números complejos
Al trabajar con los números complejos, las ecuaciones cuadráticas siempre tienen dos soluciones, las cuales son z1 y z2 donde z2 es el conjugado de z1. Además, se pueden clasificar en:
-Complejos: las soluciones son de la forma z=p±qi, donde p y q son números reales. Este caso corresponde al primer caso de la lista anterior.
-Complejos Puros: es cuando la parte real de la solución es igual a cero, es decir que la solución tiene la forma z=±qi, donde q es un número real. Este caso corresponde al primer caso de la lista anterior.
-Complejos con parte imaginaria igual a cero: es cuando la parte compleja de la solución es igual a cero, es decir que la solución es un número real. Este caso corresponde a los dos últimos casos de la lista anterior.
¿Cómo se calculan las soluciones de una ecuación cuadrática?
Para calcular las soluciones de una ecuación cuadrática se utiliza una fórmula conocida como “la resolvente” que dice que las soluciones de una ecuación ax²+bx+c=0 vienen dadas por la expresión de la siguiente imagen:

La cantidad que aparece dentro de la raíz cuadrada es llamada el discriminante de la ecuación cuadrática y es denotado por la letra “d”.
La ecuación cuadrática tendrá:
-Dos soluciones reales si, y solo si, d>0.
-Una solución real repetida si, y solo si, d=0.
-Cero soluciones reales (o dos soluciones complejas) si, y solo si, d0.
Ejemplos
-Las soluciones de la ecuación x²+x-2=0 vienen dadas por:
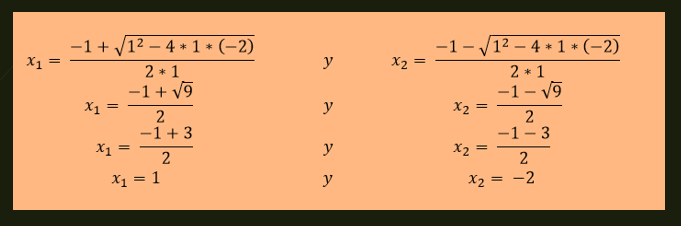
-La ecuación x²-4x+4=0 tiene una solución repetida la cual viene dada por:
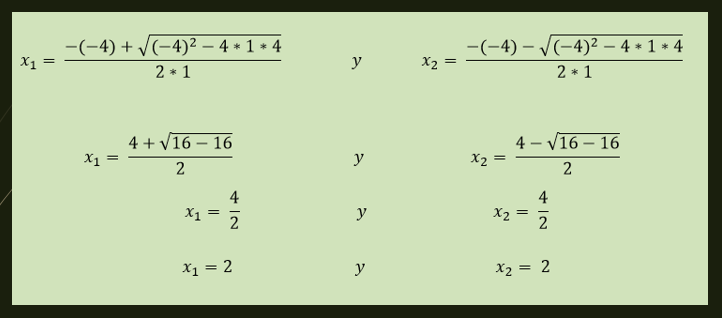
-Las soluciones de la ecuación x²+1=0 vienen dadas por:
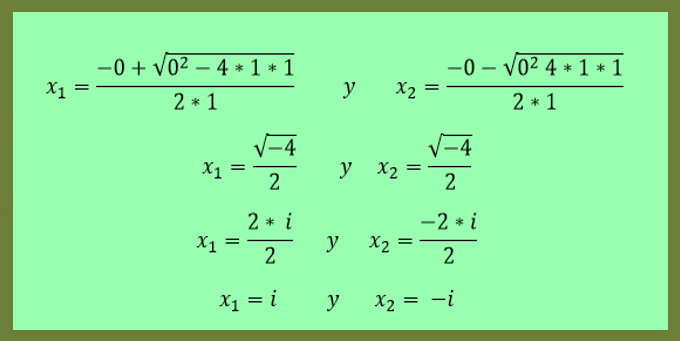
Como se puede apreciar en este último ejemplo, x2 es el conjugado de x1.
