Triángulo isósceles: qué es, características, propiedades, cálculos

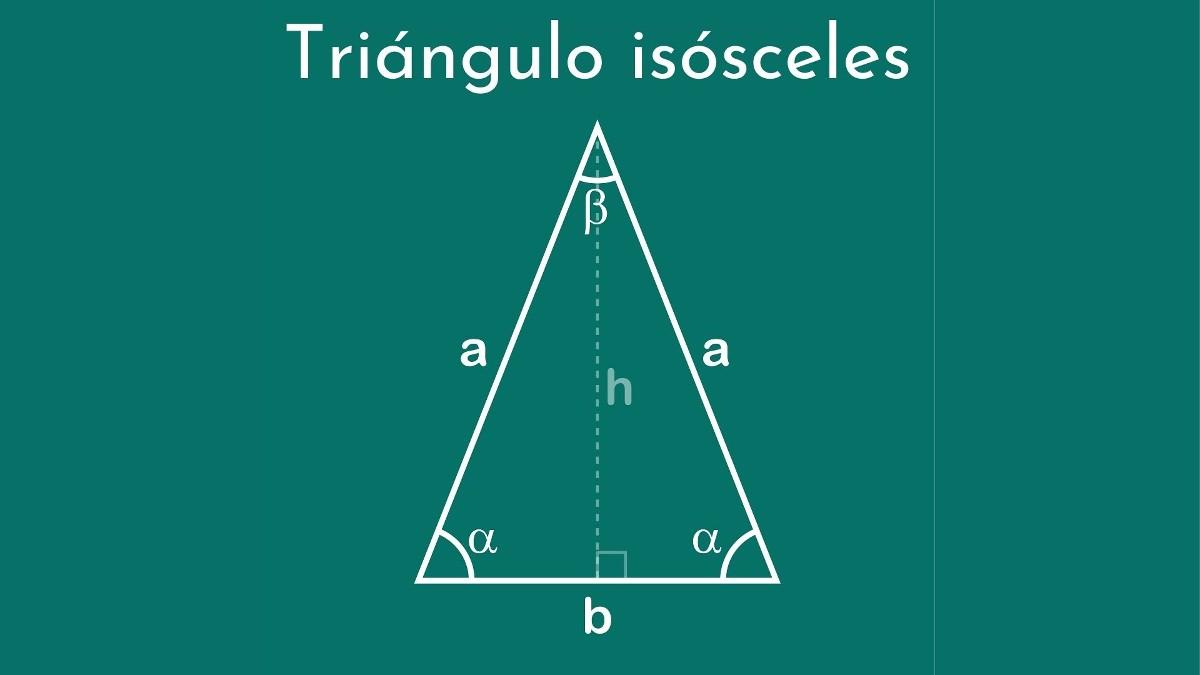
¿Qué es un triángulo isósceles?

Un triángulo isósceles es un polígono de tres lados, donde dos de ellos tienen la misma medida y el tercer lado una medida diferente. Este último lado es llamado base. Debido a esta característica se le dio este nombre, que en griego significa “piernas iguales”.

Los triángulos son polígonos considerados como los más simples en la geometría, porque están formados por tres lados, tres ángulos y tres vértices. Son los que poseen el menor número de lados y ángulos con respecto a los demás polígonos, sin embargo su uso es muy extenso.

Características de los triángulos isósceles

El triángulo isósceles fue clasificado usando como parámetro la medida de sus lados, ya que dos de sus lados son congruentes, es decir, tienen la misma longitud.

Según la amplitud de los ángulos internos, los triángulos isósceles se clasifican en:

• Triángulo rectángulo isósceles: dos de sus lados son iguales. Uno de sus ángulos es recto (90^o) y los otros son iguales (45^o cada uno)
• Triángulo obtusángulo isósceles: dos de sus lados son iguales. Uno de sus ángulos es obtuso (> 90^o).
• Triángulo acutángulo isósceles: dos de sus lados son iguales. Todos sus ángulos son agudos ( 90^o), donde dos tienen la misma medida.

Componentes

• La mediana: es una recta que sale desde el punto medio de un lado y llega al vértice opuesto. Las tres medianas concurren en un punto llamado baricentro o centroide.
• La bisectriz: es una semirrecta que divide el ángulo de cada vértice en dos ángulos de igual medida. Por eso es conocido como eje de simetría, y este tipo de triángulos posee solo uno.
• La mediatriz: es un segmento perpendicular al lado del triángulo, que tiene origen en la mitad de este. Existen tres mediatices en un triángulo y concurren en un punto llamado circuncentro.
• La altura: es la recta que va desde el vértice hasta el lado que es opuesto y además esta recta es perpendicular a dicho lado. Todos los triángulos tienen tres alturas, las cuales coinciden en un punto llamado ortocentro.

Propiedades de los triángulos isósceles

Los triángulos isósceles son definidos o identificados porque tienen varias propiedades que los representan, originadas de los teoremas propuestos por grandes matemáticos:

Ángulos internos

La suma de los ángulos internos es siempre igual a 180^o.

Suma de los lados

La suma de las medidas de dos lados siempre debe ser mayor que la medida del tercer lado, a + b > c.

Lados congruentes

Los triángulos isósceles tienen dos lados con la misma medida o longitud; es decir, son congruentes, y el tercer lado es diferente a estos.

Ángulos congruentes

Los triángulos isósceles también son conocidos como triángulos isoángulos, porque tienen dos ángulos que poseen la misma medida (congruentes). Estos se ubican en la base del triángulo, de forma opuesta a los lados que tienen la misma longitud.

Debido a esto, se generó el teorema que establece que:

“si un triángulo tiene dos lados congruentes, los ángulos opuestos a esos lados también serán congruentes”. Por lo tanto, si un triángulo es isósceles los ángulos de sus bases son congruentes.

Ejemplo:

En la siguiente figura se observa un triángulo ABC. Al trazar su bisectriz desde el vértice del ángulo B hasta la base, el triángulo es divido en dos triángulos iguales BDA y BDC:

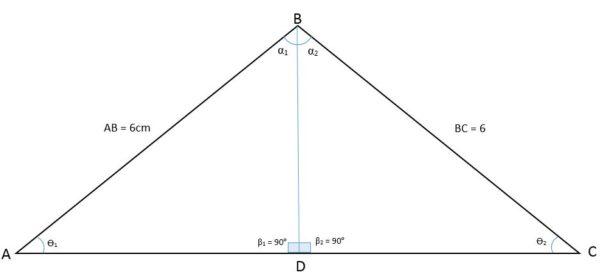
De esa forma, el ángulo del vértice B también fue dividido en dos ángulos iguales. La bisectriz ahora es el lado (BD) común entre esos dos nuevos triángulos, mientras que los lados AB y BC son los lados congruentes. Así se tiene el caso de congruencia lado, ángulo, lado (LAL).

Con eso se demuestra que los ángulos de los vértices A y C tienen la misma medida, así como también se puede demostrar que como los triángulos BDA y BDC son congruentes, los lados AD y DC también lo son.

Altura, mediana, mediatriz y bisectriz son coincidentes

La recta trazada desde el vértice opuesto a la base hasta el punto medio de la base del triángulo isósceles, es a la vez la altura, la mediana y  la mediatriz, así como también la bisectriz relativa al ángulo opuesto de la base.

Todos estos segmentos coinciden en uno solo que los representa.

Ejemplo:

En la siguiente figura se observa el triángulo ABC con un punto medio M que divide la base en dos segmentos BM y CM.

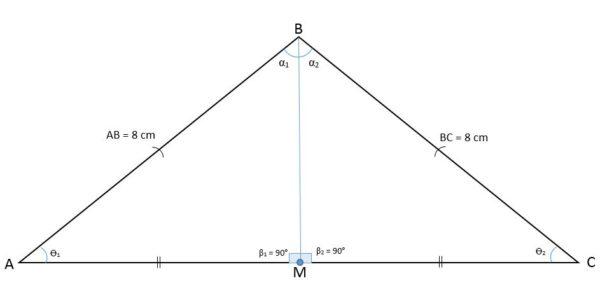
Al trazar un segmento desde el punto M hasta el vértice opuesto, por definición se obtiene la mediana AM, que es relativa al vértice A y al lado BC.

Como el segmento AM divide al triángulo ABC en dos triángulos iguales AMB y AMC, significa que se tendrá el caso de congruencia lado, ángulo, lado, y por tanto AM también será la bisectriz de BÂC.

Por eso la bisectriz será siempre igual a la mediana y viceversa.

El segmento AM forma ángulos que tienen la misma medida para los triángulos AMB y AMC; es decir, son suplementarios, de tal forma que la medida de cada uno será:

Med. (AMB) + Med. (AMC) = 180^o

2 _* Med. (AMC) = 180^o

Med. (AMC) =180^o ÷ 2

Med. (AMC) = 90^o

Se puede saber que los ángulos formados por el segmento AM con respecto a la base del triángulo son rectos, lo que indica que ese segmento es totalmente perpendicular a la base.

Por lo tanto representa la altura y la mediatriz, sabiendo que M es el punto medio.

Por lo tanto, la recta AM:

• Representa la altura de BC.
• Es mediana.
• Está contenida dentro de la mediatriz de BC.
• Es la bisectriz del ángulo del vértice Â

Alturas relativas

Las alturas que son relativas a los lados iguales, tienen la misma medida también.

Como el triángulo isósceles tiene dos lados iguales, sus dos alturas respectivas también serán iguales.

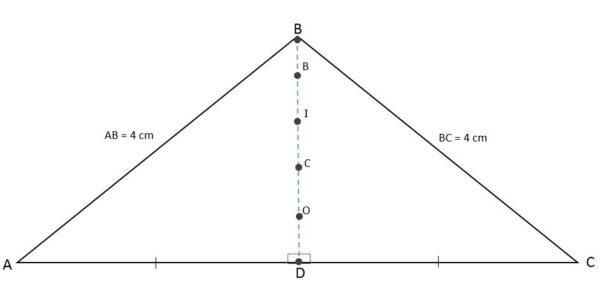
Ortocentro, baricentro, incentro y circuncentro coincidentes

Como la altura, mediana, bisectriz y mediatriz relativas a la base son representadas a la vez por un mismo segmento, el ortocentro, baricentro, incentro y circuncentro serán puntos colineales, es decir, se encontrarán en la misma recta:

Cálculo de los triángulos isósceles

¿Cómo calcular el perímetro?

El perímetro de un polígono es calculado mediante la suma de los lados.

Como en este caso el triángulo isósceles tiene dos lados con la misma medida, su perímetro se calcula con la siguiente fórmula:

P = 2_*(lado a) + (lado b).

¿Cómo calcular la altura?

La altura es la recta perpendicular a la base, divide al triángulo en dos partes iguales al prolongarse hasta el vértice opuesto.

La altura representa al cateto opuesto (a), la mitad de la base (b/2) al cateto adyacente y el lado “a” representa a la hipotenusa.

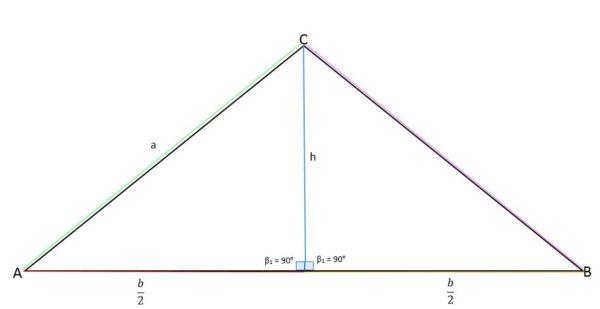
Utilizando el teorema de Pitágoras, se puede determinar el valor de la altura:

a² + b² = c²

Donde:

a² = altura (h).

b² = b / 2.

c² = lado a.

Sustituyendo esos valores en el teorema de Pitágoras, y despejando la altura se tiene:

h² + (b / 2)² = a²

h² + b² / 4 = a²

h² = a² – b² / 4

h = √ (a² – b² / 4).

Si es conocido el ángulo que forman los lados congruentes, la altura puede ser calculada con la siguiente fórmula:

¿Cómo calcular el área?

El área de los triángulos siempre se calcula con la misma fórmula, multiplicando la base por altura y dividiendo entre 2:

Existen casos donde solo se conocen las medidas de dos lados del triángulo y el ángulo que se forma entre ellos. En este caso, para determinar el área es necesario aplicar las razones trigonométricas:

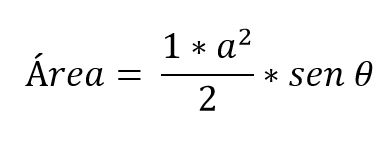
¿Cómo calcular la base del triángulo?

Como el triángulo isósceles tiene dos lados iguales, para determinar el valor de su base se necesita saber por lo menos la medida de la altura o uno de sus ángulos.

Conociendo la altura se utiliza el teorema de Pitágoras:

a² + b² = c²

Donde:

a² = altura (h).

c² = lado a.

b² = b / 2, es desconocida.

Despejamos b² de la fórmula y tenemos que:

b² = a² – c²

b = √ a² – c²

Como ese valor corresponde a la mitad de la base, se debe multiplicar por 2 para obtener la medida completa de la base del triángulo isósceles:

b = 2 _* (√ a² – c²)

En el caso de que se conozca solo el valor de sus lados iguales y el ángulo entre estos, se aplica la trigonometría, trazando una recta desde el vértice hasta la base que divida al triángulo isósceles en dos triángulos rectángulos.

De esa forma la mitad de la base es calculada con:

También es posible que solo sean conocidos el valor de la altura y ángulo del vértice que está opuesto a la base. En ese caso, por trigonometría se puede determinar la base:

Ejercicios

Primer ejercicio

Hallar el área del triángulo isósceles ABC, sabiendo que dos de sus lados miden 10 cm y el tercer lado mide 12 cm.

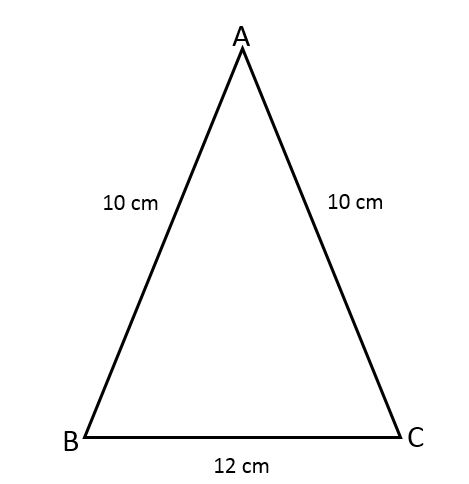
Solución

Para hallar el área del triángulo es necesario calcular la altura usando la fórmula del área que se relaciona con el teorema de Pitágoras, ya que no se conoce el valor del ángulo formado entre los lados iguales.

Se tienen los siguientes datos del triángulo isósceles:

• Lados iguales (a) = 10 cm.
• Base (b) = 12 cm.

Se sustituyen los valores en la fórmula:

Segundo ejercicio

La longitud de los dos lados iguales de un triángulo isósceles mide 42 cm, la unión de estos lados forma un ángulo de 130^o. Determinar el valor del tercer lado, el área de ese triángulo y el perímetro.

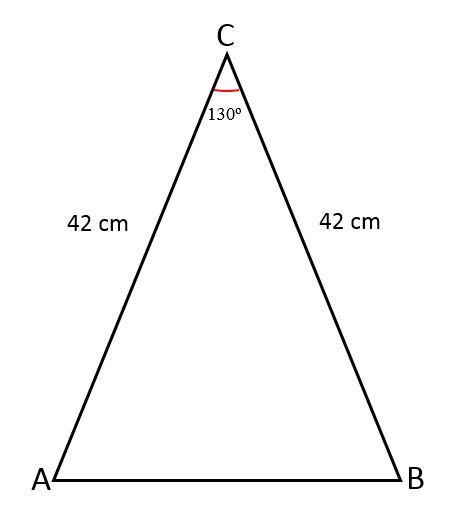
Solución

En este caso se conocen las medidas de los lados y el ángulo entre estos.

Para conocer el valor del lado faltante, es decir, la base de ese triángulo, se traza una recta perpendicular a esta, dividiendo el ángulo en dos partes iguales, uno para cada triángulo rectángulo que se forma.

• Lados iguales (a) = 42 cm.
• Ángulo (Ɵ) = 130^o

Ahora, por trigonometría, se calcula el valor de la mitad de la base, que corresponde a la mitad de la hipotenusa:

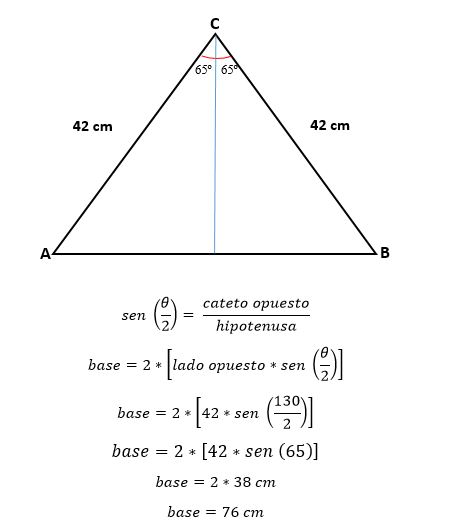
Para calcular el área es necesario saber la altura de ese triángulo, que puede ser calculada por trigonometría o por el teorema de Pitágoras, ahora que ya se determinó el valor de la base.

Por trigonometría será:

El perímetro se calcula:

P = 2_*(lado a) + (lado b).

P = 2_* (42 cm) + (76 cm)

P = 84 cm + 76 cm

P = 160 cm.

Tercer ejercicio

Calcular los ángulos internos del triángulo isósceles, sabiendo que el ángulo de la base es Â= 55^o

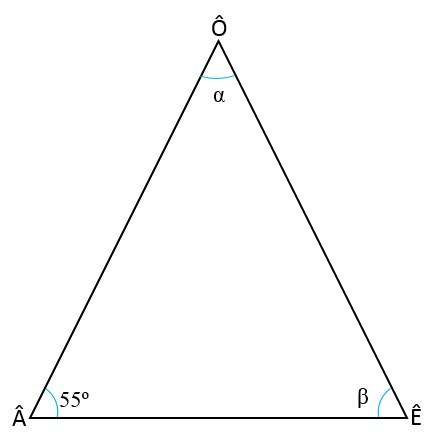
Solución

Para hallar los dos ángulos que faltan (Ê y Ô) es necesario recordar dos propiedades de los triángulos:

• La suma de los ángulos internos de todo triángulo siempre será = 180^o:

 + Ê + Ô = 180 ^o

• En un triángulo isósceles los ángulos de la base siempre son congruentes, es decir, tienen la misma medida, por lo tanto:

 = Ô

Ê = 55^o

Para determinar el valor del ángulo Ê, se sustituyen los valores de los otros ángulos en la primera regla y se despeja Ê:

55^o + 55^o + Ô= 180 ^o

110 ^o + Ô = 180 ^o

Ô = 180 ^o – 110 ^o

Ô = 70 ^o.

Referencias

1. Álvarez, E. (2003). Elementos de geometría: con numerosos ejercicios y geometría del compás. Universidad De Medellin.
2. Álvaro Rendón, A. R. (2004). Dibujo Técnico: cuaderno de actividades.
3. Ángel, A. R. (2007). Algebra Elemental. Pearson Educación.
4. Arthur Goodman, L. H. ( 1996). Algebra y trigonometría con geometría analítica. Pearson Educación.
5. Baldor, A. (1941). Álgebra. La Habana: Cultura.
6. José Jiménez, L. J. (2006). Matematicas 2.
7. Tuma, J. (1998). Engineering Mathematics Handbook. Wolfram MathWorld.