Ángulos en la circunferencia: tipos, propiedades, ejercicios resueltos
Se llaman ángulos de la circunferencia a aquellos en los que alguno de sus elementos están o intersecan a una circunferencia dada. Entre ellos están los siguientes:
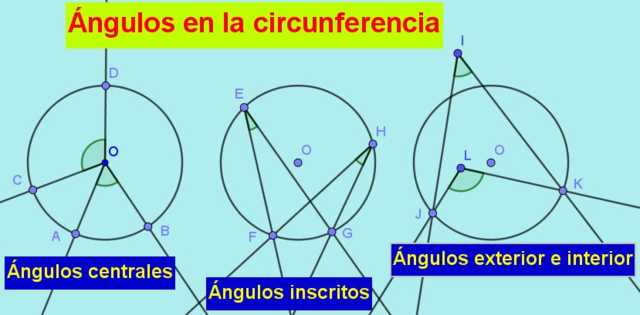
1.- El ángulo central, cuyo vértice está en el centro de la circunferencia y sus lados son secantes a la misma, tal como lo vemos en la siguiente imagen:
2.- El ángulo inscrito, cuyo vértice está sobre la circunferencia y sus lados son secantes o tangente a la circunferencia.
3.- Ángulo exterior, cuyo vértice está fuera de la circunferencia pero sus lados son secantes o tangentes a la circunferencia.
4.- El ángulo interior, con el vértice al interior de la circunferencia y sus lados secante a la misma.
Todos estos ángulos guardan ciertas relaciones entre sí y esto nos lleva a importantes propiedades entre los ángulos pertenecientes a una circunferencia dada.
Índice del artículo
El ángulo central se define como aquel cuyo vértice está en el centro de la circunferencia y sus lados cortan a la circunferencia.
La medida en radianes de un ángulo central es el cociente entre el arco que subtiende, es decir el arco de circunferencia comprendido entre los lados del ángulo, y el radio de la circunferencia.
Si la circunferencia es unitaria, es decir de radio 1, entonces la medida del ángulo central es la longitud del arco, la cual se corresponde con el número de radianes.
Si se quiere la medida del ángulo central en grados, entonces se multiplica la medida en radianes por el factor 180º/π.
Los instrumentos de medición de ángulos, como el transportador y el goniómetro, siempre usan un ángulo central y la longitud del arco subtendido.
Están calibrados en grados sexagesimales, lo que significa que siempre que se mide un ángulo con ellos, en el fondo lo que se mide es la longitud del arco subtendido por el ángulo central.
Propiedad
La medida de un ángulo central en radianes es igual a la longitud del arco que subtiende o intercepta dividido entre la longitud del radio.
El ángulo inscrito de una circunferencia es aquel que tiene su vértice sobre la circunferencia y sus semirrectas son secantes o tangentes a la misma.
Sus propiedades son:
Propiedades
-El ángulo inscrito es convexo o plano.
–Cuando un ángulo inscrito intercepta el mismo arco que el ángulo central, la medida del primero será la mitad de la del segundo.
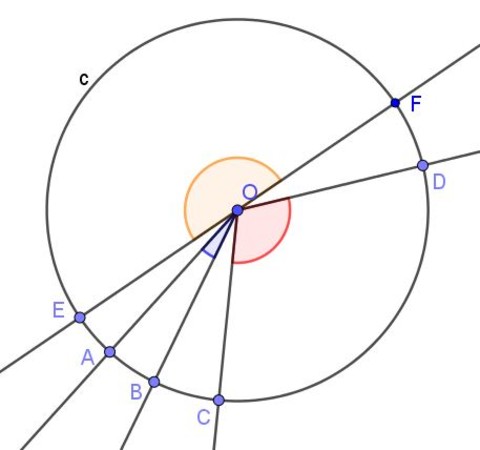
En la figura 3 se muestran dos ángulos ∠ABC y ∠AOC que interceptan el mismo arco de circunferencia A⌒C.
Si la medida del ángulo inscrito es α, entonces la medida β del ángulo central es el doble de la medida del ángulo inscrito (β = 2 α) debido a que ambos subtienden el mismo arco de medida d.
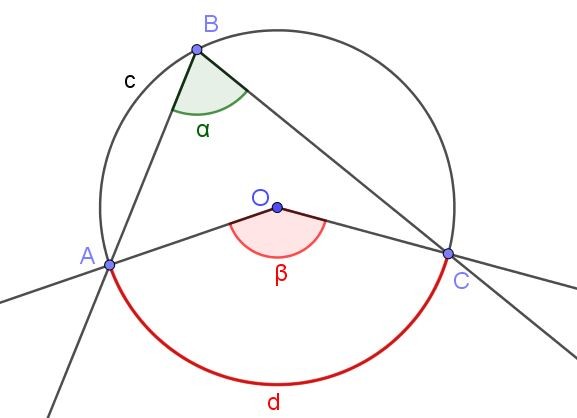
Es el ángulo cuyo vértice es exterior a la circunferencia y cada uno de sus lados corta a la circunferencia en uno o más puntos.
Propiedad
-Su medida es igual a la semidiferencia (o diferencia dividida entre 2) de los ángulos centrales que interceptan los mismos arcos.
Para asegurar que la medida sea positiva, la semidiferencia siempre debe ser la del ángulo central de mayor medida menos la medida del ángulo central menor, tal como se ilustra en la siguiente figura.
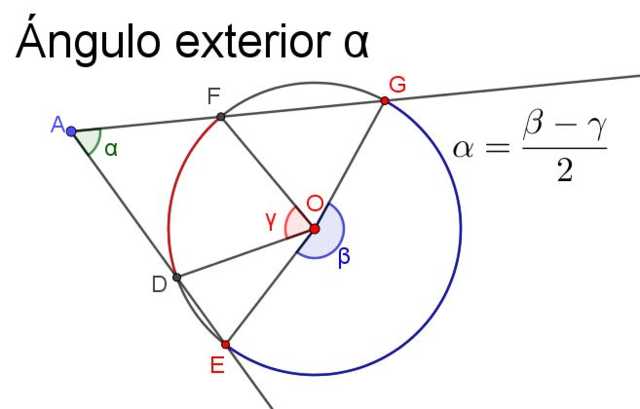
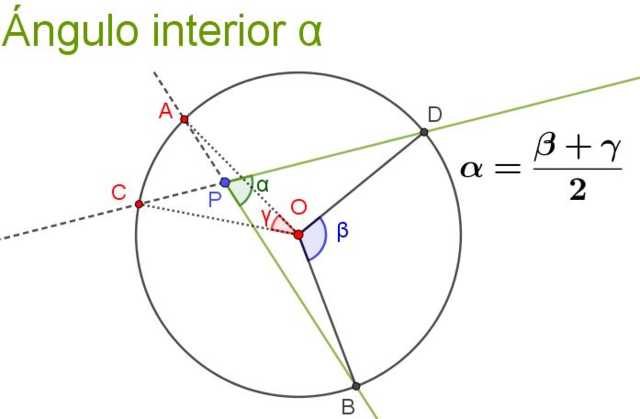
El ángulo interior es aquel cuyo vértice está en el interior de la circunferencia y sus lados cortan a la circunferencia.
Propiedad
Su medida es igual a la semisuma del ángulo central que subtiende el mismo arco, más el ángulo central que subtiende el mismo arco que su ángulo prolongación (este es el ángulo interior formado por las semirrectas complementarias a las del ángulo interior original).
La siguiente figura ilustra y aclara la propiedad del ángulo interior.
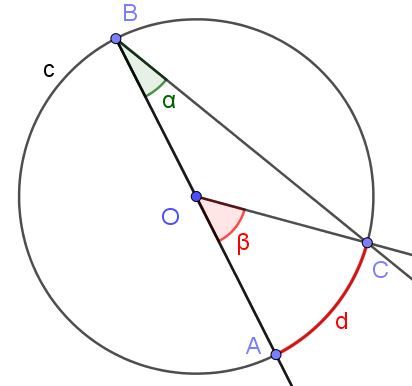
Suponga un ángulo inscrito en el que uno de sus lados pasa por el centro de la circunferencia, tal como lo muestra la figura 6. El radio de la circunferencia es OA = 3 cm y el arco d tiene una longitud de π/2 cm. Determine el valor de los ángulos α y β.
Solución
En este caso, se forma el triángulo isósceles COB, ya que [OC] = [OB]. En un triángulo isósceles los ángulos adyacentes a la base son iguales, por lo tanto se tienen que ∠BCO = ∠ABC = α. Por otra parte ∠COB = 180º – β. Considerando la suma de los ángulos internos del triángulo COB se tiene:
α + α + (180º – β) = 180º
De donde se deduce que 2 α = β, o lo que es equivalente α = β/2, con lo que se confirma la propiedad (3) de la sección previa, que la medida del ángulo inscrito es la mitad del ángulo central, cuando ambos ángulos subtienden la misma cuerda [AC].
Ahora pasamos a determinar los valores numéricos: el ángulo β es central y su medida en radianes es el cociente entre el arco d y el radio r = OA, por lo que su medida es:
β = d / r = (π/2 cm) / (3 cm) = π/6 rad = 30º.
Por otra parte ya se había afirmado que α = β / 2 = (π/6 rad) / 2 = π/12 rad = 15º.
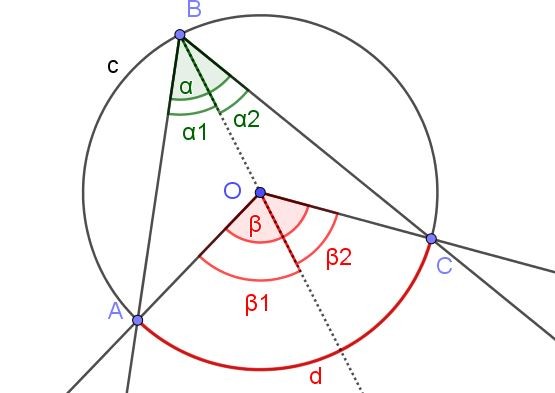
En la figura 7 los ángulos α1 y β2 tienen la misma medida. Además el ángulo β1 mide 60º. Determine los ángulos β y α.
Solución
En este caso se tiene un ángulo inscrito ∠ABC en el que el centro O de la circunferencia está dentro del ángulo.
Debido a la propiedad (3) se tiene α2 = β2 /2 y α1 = β1 /2. Como:
α = α1 + α2 y β = β1 + β2
Se tiene por tanto que:
α = α1 + α2 = β1 /2 + β2 /2 = (β1 + β2) / 2 = β / 2.
Es decir, de acuerdo a las propiedades:
α = β / 2
Como se nos dice que β1 = 60º entonces:
α1 = β1 /2 = 60º / 2 = 30º.
También nos dicen que α1 = β2 por lo que se deduce que:
β2 = 30º.
El ángulo β resulta:
β1 + β2 = 60º + 30º = 90º.
Y como α = β / 2, entonces:
α= 90º / 2 = 45º.
En conclusión:
β = 90º y α = 45º.
- Baldor, A. 1973. Geometría y trigonometría. Editorial Cultural Centroamericana.
- E. A. 2003. Elementos de geometría: con ejercicios y geometría del compás. Universidad De Medellín.
- Geometría 1ro ESO. Ángulos en la circunferencia. Recuperado de: edu.xunta.es.
- Todo Ciencia. Ejercicios resueltos de ángulos en la circunferencia. Recuperado de: francesphysics.blogspot.com
- Wikipedia. Ángulo inscrito. Recuperado de: es.wikipedia.com
