Absortividad molar: qué es, ecuación, cálculo, ejercicios resueltos
¿Qué es la absortividad molar?
La absortividad molar es una propiedad química que indica cuánta luz puede absorber una especie en solución. Es decir, es una unidad que mide la capacidad de una disolución de absorber luz.
Como la luz se compone de fotones con energías (o longitudes de onda) propias, dependiendo de la especie o mezcla analizada, un fotón puede absorberse en mayor grado que otro. Quiere decir que la luz se absorbe a ciertas longitudes de onda características de la sustancia.
Así, el valor de la absortividad molar es directamente proporcional al grado de absorción de la luz a una determinada longitud de onda. Si la especie absorbe poca luz roja, su valor de absortividad será bajo. Si hay una pronunciada absorción de la luz roja, la absortividad tendrá un valor elevado.
Una especie que absorbe luz roja reflejará un color verde. Si el color verde es muy intenso y oscuro, significa que hay una fuerte absorción de la luz roja.
No obstante, algunas tonalidades de verde pueden deberse a los reflejos de diferentes gamas de amarillos y azules, los cuales se mezclan y se perciben como verdes turquesas, esmeralda, vidrio, etc.
Ecuación de la absortividad molar
La absortividad molar es una constante definida en la expresión matemática de la ley de Lambert-Beer, y señala simplemente cuánta luz absorbe la especie química o la mezcla. La ecuación es:
A = εbc
Donde A es la absorbancia de la solución a una longitud de onda λ seleccionada, b es la longitud de la celda donde se contiene la muestra a analizar, y, por tanto, es la distancia que la luz atraviesa dentro de la solución, c es la concentración de la especie absorbente, y ε, la absortividad molar.
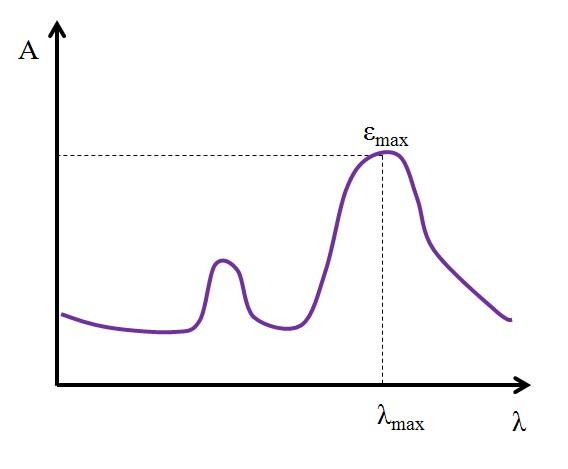
Dada λ, expresada en nanómetros, el valor de ε permanece constante. Pero al cambiar los valores de λ, es decir, al medir las absorbancias con luces de otras energías, ε cambia, alcanzando un valor mínimo o máximo.
Si se conoce su valor máximo, εmax, se determina al mismo tiempo λmax. Esto es, la luz que más absorbe la especie:
Unidades
Para conocer las unidades de ε, hay que saber que las absorbancias son valores adimensionales, y, por lo tanto, la multiplicación de las unidades de b y c debe anularse.
La concentración de la especie absorbente puede expresarse bien sea en g/L o mol/L, y b usualmente se expresa en cm o m (porque es la longitud de la celda que atraviesa el haz de luz). La molaridad es igual a mol/L, por lo que c también se expresa como M.
Así, multiplicando las unidades de b y c se obtiene: M∙cm. Las unidades que debe tener ε para dejar adimensional el valor de A son aquellas que al multiplicar M∙cm dé un valor de 1 (M∙cm x U=1).
Despejando U, se obtiene sencillamente M-1∙cm-1, que también puede escribirse como: L∙mol-1∙cm-1.
De hecho, utilizar las unidades M-1∙cm-1 o L∙mol-1∙cm-1 agiliza los cálculos para determinar la absortividad molar. Sin embargo, también suele expresarse con unidades de m2/mol o cm2/mol.
Cuando viene expresada con estas unidades, debe recurrirse a algunos factores de conversión para modificar las unidades de b y c.
¿Cómo calcular la absortividad molar?
Despeje directo
La absortividad molar puede calcularse directamente mediante su despeje en la ecuación anterior:
ε= A/bc
Si se conoce la concentración de la especie absorbente, la longitud de la celda, y cuál es la absorbancia obtenida a una longitud de onda, puede calcularse ε. Sin embargo, esta forma de calcular arroja un valor inexacto y poco confiable.
Método de graficación
Si se observa detenidamente la ecuación de la ley de Lambert-Beer, se notará que se parece a la ecuación de una recta (Y=aX+b).
Esto significa que si se grafican los valores de A en el eje Y, y los de c en el eje X, debe obtenerse una línea recta que pasa por el origen (0,0). Así, A vendría a ser Y, X sería c, y a equivaldría a εb.
Por lo tanto, graficada la recta, basta con tomar dos puntos cualquiera para determinar la pendiente, es decir, a. Una vez hecho esto, y conocida la longitud de la celda, b, resulta fácil despejar el valor de ε.
A diferencia del despeje directo, graficar A vs. c permite promediar las mediciones de absorbancias y disminuir el error experimental, y además, por un único punto pueden pasar infinitas rectas, por lo que no es práctico el despeje directo.
Asimismo, los errores experimentales pueden hacer que una recta no pase por dos, tres o más puntos, por lo que en realidad se utiliza la recta obtenida tras aplicar el método de los mínimos cuadrados (función que ya viene incorporada en las calculadoras).
Todo esto asumiendo una alta linealidad, y por tanto, un cumplimiento de la ley de Lamber-Beer.
Ejercicios resueltos
Ejercicio 1
Se sabe que una solución de un compuesto orgánico con una concentración de 0.008739 M presentó una absorbancia de 0.6346, medida a λ=500 nm y con una celda de 0.5 cm de longitud. Calcule cuál es la absortividad molar del complejo a dicha longitud de onda.
A partir de estos datos puede despejarse directamente ε:
ε= 0.6346/(0.5 cm)(0.008739 M)
145.23 M-1∙cm-1
Ejercicio 2
Se tiene las siguientes absorbancias medidas a diferentes concentraciones de un complejo metálico a una longitud de onda de 460 nm, y con una celda de 1 cm de longitud:
A: 0.03010 0.1033 0.1584 0.3961 0.8093
c: 1.8∙10-5 6∙10-5 9.2∙10-5 2.3∙10-4 5.6∙10-4
Calcule la absortividad molar del complejo.
Hay un total de cinco puntos. Para calcular ε es necesario graficarlos colocando los valores de A en el eje Y, y las concentraciones c en el eje X. Una vez hecho esto, se determina la recta de los mínimos cuadrados, y con su ecuación se podrá determinar ε.
En este caso, graficados los puntos y trazada la recta con un coeficiente de determinación R2 de 0.9905, la pendiente es igual a 7∙10-4, es decir, εb= 7∙10-4.
Por lo tanto, con b=1cm, ε será de 1428,57 M-1.cm-1 (1/7∙10-4).
Referencias
- Molar attenuation coefficient. Recuperado de en.wikipedia.org
- Science Struck. Molar Absorptivity. Recuperado de sciencestruck.com
- Colorimetric Analysis (Beer’s law or Spectrophotometric Analysis). Recuperado de chem.ucla.edu
