Línea vertical: características y uso en matemáticas (ejemplos)

¿Qué es una línea vertical?
Una línea vertical es aquella que sigue la dirección en la que cualquier objeto cae al suelo cuando se lo suelta desde cierta altura y es perpendicular a la línea del horizonte, ya que forma con esta un ángulo de 90º.
Al dibujarla, se hace un trazo de arriba hacia abajo o viceversa. Los bordes laterales de la pantalla de un monitor de computadora son ejemplos de líneas verticales, así como el tronco recto de muchos árboles.
En arquitectura y en diseño, la línea vertical sugiere en las personas una sensación de dinamismo, movimiento, poder y elevación, en contraposición con las líneas horizontales, que sugieren descanso y relajación. Cuando alguien está erguido, es decir, su posición es vertical y perpendicular respecto al suelo, está listo para caminar, correr y en general, entrar en movimiento.
Se pueden encontrar multitud de líneas verticales en el arte, las fotografías y construcciones humanas, líneas permanentes o pasajeras, como las que se forman por contrastes entre luz y sombra sobre las paredes, a lo largo del día.
La línea vertical también se usa para describir un movimiento muy común en la naturaleza: la caída libre, así como también describir la dirección de otras fuerzas, aparte de la gravedad ya mencionada, cuando ellas actúan perpendicularmente a una determinada superficie.
Forma matemática de la línea vertical
En Matemática y Geometría, la línea vertical coincide con el eje “y” cartesiano, el eje de la variable dependiente, mientras que el eje horizontal corresponde al eje “x”, el de la variable independiente.
Una recta vertical se puede graficar fácilmente en el plano cartesiano, pues corresponde a la ecuación:
x = k
Donde k es una constante. Las rectas verticales son siempre paralelas al eje y, por ejemplo la recta x = −3 que aparece en rojo en la siguiente figura:
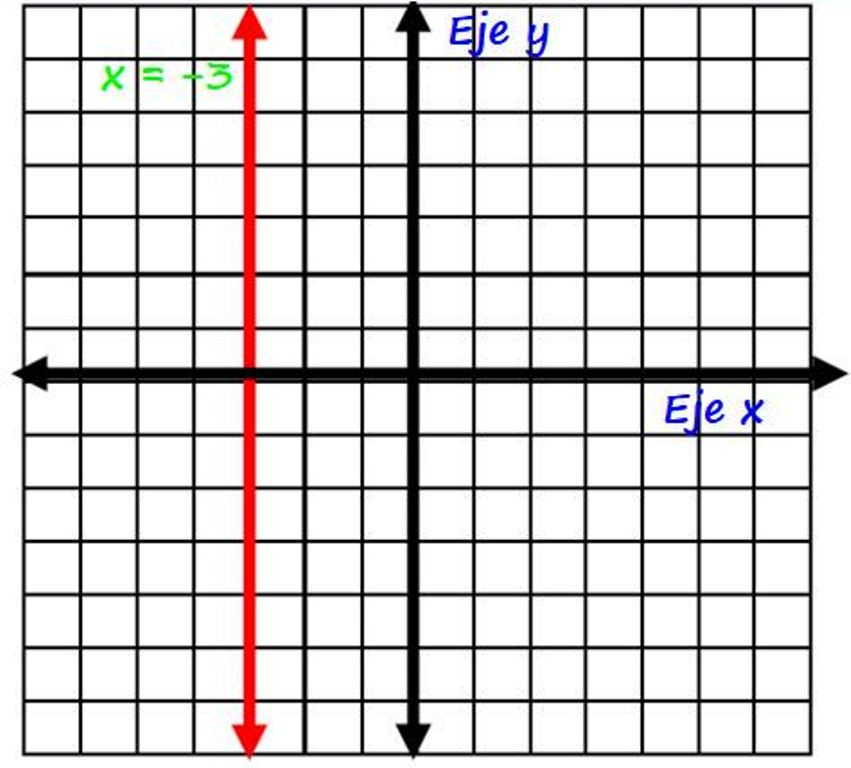
Nótese que todos los puntos de esta recta siempre tienen la misma coordenada x, por ejemplo los puntos (−3, 0); (−3, 1), (−3, 2) y más. Además la recta en color rojo corta al eje horizontal en la coordenada x = −3.
Por otra parte, la recta de ecuación x = 0 es otra manera de expresar al eje vertical o eje y.
Pendiente de una línea vertical
Se considera que una recta vertical carece de pendiente definida, o también puede decirse que la recta vertical tiene pendiente infinita, mientras que la pendiente de una recta horizontal es 0.
Cuando se trata de emplear la fórmula para calcular la pendiente de una recta: m = Δy/ Δx al calcular la pendiente de la recta vertical, ocurre que Δx siempre es igual a 0, ya que cualquier punto que se elige tiene la misma coordenada x. Recuérdese que Δx = x2 – x1, es decir, la diferencia entre las coordenadas x de dos puntos arbitrarios.
Entonces, al intentar sustituir Δx = 0 en la ecuación de la pendiente, se encuentra que:
m = Δy/ 0
Y como la división por 0 no es una operación definida, resulta que la pendiente de cualquier recta vertical es indefinida, sin importar el valor de Δy.
Prueba de la recta vertical
A diferencia de la recta horizontal, que es la gráfica de la función constante, la recta vertical x = k no es una función, ya que el mismo valor de x forma infinitos pares ordenados con los valores de y, lo cual va en contra de la definición de función (en esta, un valor de x tiene una y solo una imagen en y).
Sin embargo, la recta vertical se puede utilizar para determinar visualmente si una curva en el plano constituye o no una función. El criterio es muy simple: se traza una vertical que corte la curva en cuestión. Si lo hace en más de un punto, no es una función.
Por ejemplo, considérese la curva que se muestra a continuación, de la que se quiere saber si corresponde a la gráfica de alguna función.
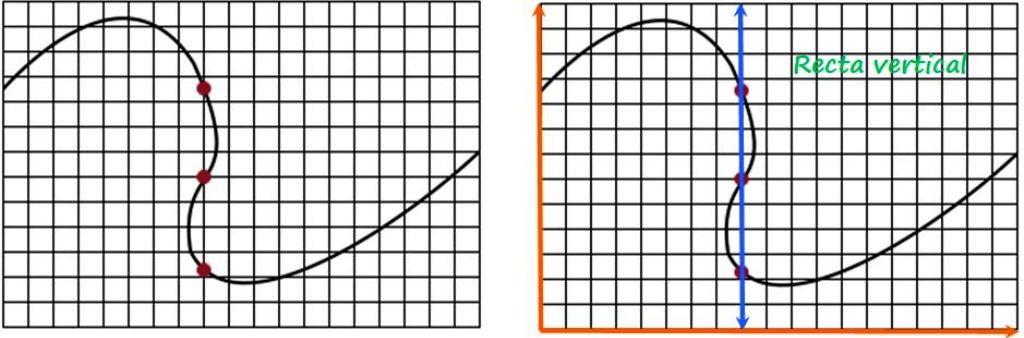
Por los puntos rojos pasa una misma recta vertical y dado que corta a la curva en más de un punto, se concluye que no es la gráfica de una función.
Asíntotas verticales
Son rectas verticales que la gráfica de una función no puede atravesar. Surgen debido a que cuando se acerca a un determinado valor de x, la función crece o decrece indefinidamente. Por supuesto, este valor de x no pertenece al dominio de la función.
Cuando se trata de una función racional, los valores de x que originan asíntotas verticales son los que anulan el denominador. En tal caso, al intentar sustituir en la función ese valor de x, quedaría una división entre 0, la cual no es posible realizar, como se explicó anteriormente.
Ahora bien, lo que sí es posible hacer es dividir una cantidad finita entre otra cantidad tan pequeña como se quiera, siempre que la cantidad no sea exactamente 0.
En tales casos, el resultado de la división puede ser un número sumamente grande (o pequeño por ser negativo, depende del signo del numerador). El lector puede comprobar esto dividiendo por ejemplo:
2 ÷ 0.000001 = 2 000 000
Supóngase que el valor de x que anula al denominador de la función racional es x = b. Cuando en la función se sustituye un valor muy cercano a b (pero no exactamente b), se origina una división entre una cantidad finita y otra sumamente pequeña.
Es por eso que la función racional tiende a infinito positivo o a infinito negativo en las cercanías de la asíntota vertical, dependiendo del valor de x usado para acercarse a b.
Ejemplo de asíntota vertical
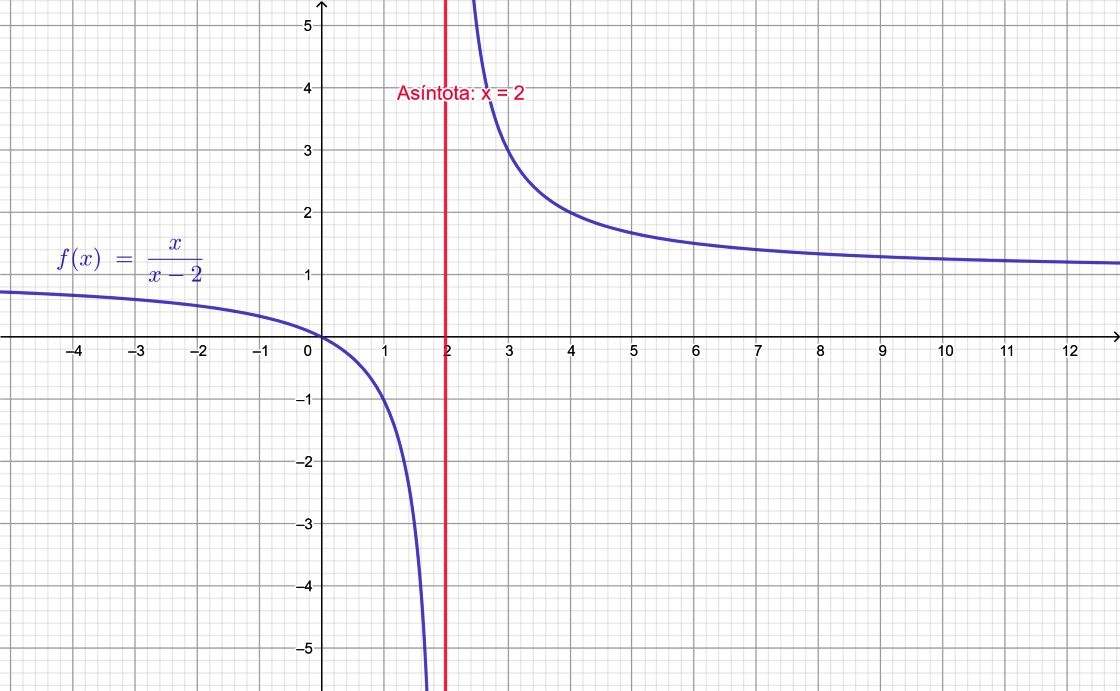
Se comprueba lo anterior con la función racional:
Esto fue un acercamiento a x = 2 desde la izquierda y el resultado es que la función se hace muy negativa, es decir, tiende a infinito negativo. Ahora se puede probar con un acercamiento por la derecha, por ejemplo x = 2.0001:
Y se ve que la función se aleja hacia infinito positivo. La gráfica lo confirma:
Referencias
- Atlantic Union Conference Teacher Bulletin. Horizontal and vertical lines. Recuperado de: teacherbulletin.org.
- Byju’s. Vertical line. Recuperado de: byjus.com.
- CK-12. Graficación de rectas horizontales y verticales. Recuperado de: ck-12.org.
- Stewart, J. 2006. Pre-cálculo: Matemáticas para el Cálculo. 5ta. Edición. Cengage Learning.
- Zill, D. 1984. Álgebra y Trigonometría. 1ra. Edición. McGraw Hill.
