Distribución F: características y ejercicios resueltos
La distribución F o distribución de Fisher-Snedecor es la que se usa para comparar las varianzas de dos poblaciones diferentes o independientes, cada una de las cuales sigue una distribución normal.
La distribución que sigue la varianza de un conjunto de muestras de una sola población normal es la distribución ji-cuadrada (Χ2) de grado n-1, si cada una de las muestras del conjunto tiene n elementos.
Para comparar las varianzas de dos poblaciones diferentes, es necesario definir un estadístico, es decir una variable aleatoria auxiliar que permita discernir si ambas poblaciones tienen o no igual varianza.
Dicha variable auxiliar puede ser directamente el cociente de las varianzas muestrales de cada población, en cuyo caso, si dicho cociente es cercano a la unidad, se tiene evidencia que ambas poblaciones tienen varianzas semejantes.
Índice del artículo
- 1 El estadístico F y su distribución teórica
- 2 Manejo de la distribución F
- 3 Ejercicios resueltos
- 4 Referencias
La variable aleatoria F o estadístico F propuesto por Ronald Fisher (1890 – 1962) es el que se usa más frecuentemente para comparar las varianzas de dos poblaciones y se define de la siguiente manera:
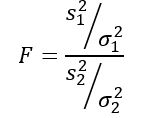
Siendo s2 la varianza muestral y σ2 la varianza poblacional. Para distinguir cada uno de los dos grupos poblacionales, se utilizan los subíndices 1 y 2 respectivamente.
Se sabe que la distribución ji-cuadrada con (n-1) grados de libertad es la que sigue la variable auxiliar (o estadístico) que se define a continuación:
X2 = (n-1) s2 / σ2.
Por lo tanto, el estadístico F sigue una distribución teórica dada por la siguiente fórmula:
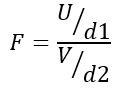
Siendo U la distribución ji-cuadrada con d1 = n1 – 1 grados de libertad para la población 1 y V la distribución ji-cuadrada con d2 = n2 – 1 grados de libertad para la población 2.
El cociente definido de esta forma es una nueva distribución de probabilidad, conocida como distribución F con d1 grados de libertad en el numerador y d2 grados de libertad en el denominador.
Media
La media de la distribución F se calcula de la siguiente manera:
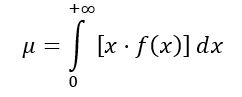
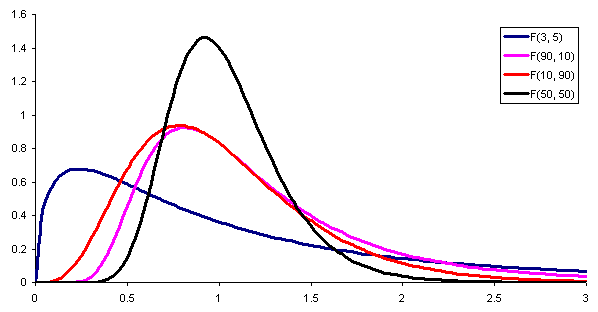
Siendo f(x) la densidad de probabilidad de la distribución F, la cual se muestra en la figura 1 para varias combinaciones de parámetros o grados de libertad.
Se puede escribir la densidad de probabilidad f(x) en función de la función Γ ( función gamma):
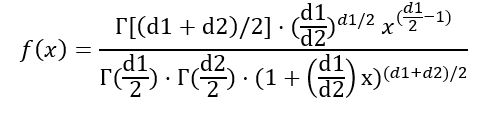
Una vez efectuada la integral indicada antes, se concluye que la media de la distribución F con grados de libertad (d1, d2) es:
μ = d2 / (d2 – 2) con d2 > 2
Donde se nota que, curiosamente, la media no depende de los grados de libertad d1 del numerador.
Moda
Por otra parte, la moda sí depende de d1 y d2 y está dada por:
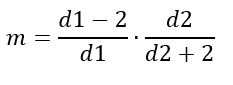
Para d1 > 2.
Varianza de la distribución F
La varianza σ2 de la distribución F se calcula a partir de la integral:
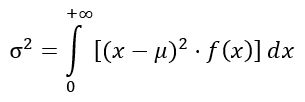
Obteniéndose:
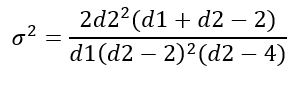
Al igual que otras distribuciones continuas de probabilidad que involucran funciones complicadas, el manejo de la distribución F se realiza mediante tablas o mediante software.
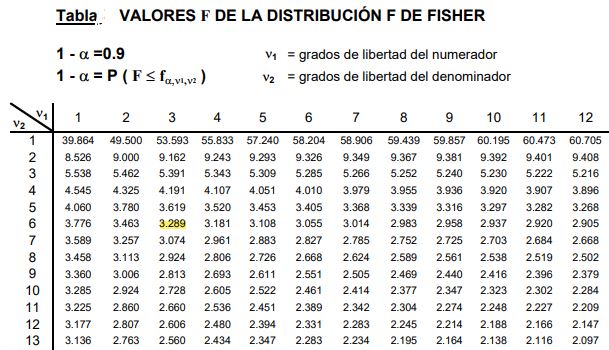
Las tablas involucran los dos parámetros o grados de libertad de la distribución F, la columna indica el grado de libertad del numerador y la fila el grado de libertad del denominador.
La figura 2 muestra una sección de la tabla de la distribución F para el caso de un nivel de significancia de 10%, es decir α = 0,1. Aparece resaltado el valor de F cuando d1= 3 y d2 = 6 con nivel de confianza 1- α = 0,9 es decir 90%.
En cuanto al software que maneja la distribución F hay una gran variedad, desde las hojas de cálculo como Excel hasta los paquetes especializados como minitab, SPSS y R por nombrar algunos de los más conocidos.
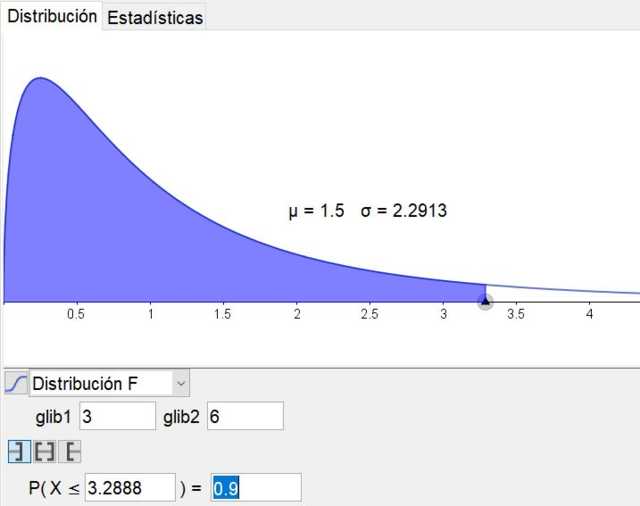
Es de resaltar que el software de geometría y matemáticas geogebra tiene una herramienta estadística que incluye las principales distribuciones, entre ellas la distribución F. La figura 3 muestra la distribución F para el caso d1= 3 y d2 = 6 con nivel de confianza de 90%.
Considere dos muestras de poblaciones que tienen la misma varianza poblacional. Si la muestra 1 tiene tamaño n1 = 5 y la muestra 2 tiene tamaño n2 = 10, determine la probabilidad teórica que el cociente de sus varianzas respectivas sea menor o igual a 2.
Solución
Debe recordarse que el estadístico F se define como:
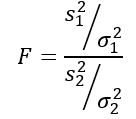
Pero se nos dice que las varianzas poblacionales son iguales, por lo que para este ejercicio se aplica:
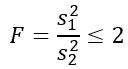
Como se desea saber la probabilidad teórica de que este cociente de varianzas muestrales sea menor o igual a 2, necesitamos conocer el área bajo la distribución F entre 0 y 2, el cual puede obtenerse por tablas o software. Para esto ha de tenerse en cuenta que la distribución F requerida tiene d1 = n1 – 1 = 5 – 1 = 4 y d2 = n2 – 1 = 10 – 1 = 9, es decir la distribución F con grados de libertad (4, 9).
Mediante el uso de la herramienta estadística de geogebra se determinó que esta área es 0.82, por lo que se concluye que la probabilidad que el cociente de varianzas muestrales sea menor o igual a 2 es del 82%.
Se tienen dos procesos de manufactura de láminas delgadas. La variabilidad del espesor debe ser lo menor posible. Se toman 21 muestras de cada proceso. La muestra del proceso A tiene una desviación estándar de 1,96 micras, mientras que la del proceso B tiene desviación estándar de 2,13 micras. ¿Cuál de los procesos tiene menor variabilidad? Utilizar un nivel de rechazo del 5%.
Solución
Los datos son los siguientes: Sb = 2,13 con nb = 21; Sa = 1,96 con na = 21. Esto significa que ha de trabajarse con una distribución F de (20, 20) grados de libertad.
La hipótesis nula implica que la varianza poblacional de ambos procesos es idéntica, es decir σa^2 / σb^2 = 1. La hipótesis alternativa implicaría varianzas poblacionales diferentes.
Entonces, bajo la suposición de varianzas poblacionales idénticas, se define el estadístico F calculado como: Fc = (Sb/Sa)^2.
Como el nivel de rechazo se ha tomado como α= 0,05, entonces α/2= 0,025
La distribución F(0.025; 20,20) = 0,406, mientras que F(0.975; 20,20) = 2,46.
Por lo tanto, la hipótesis nula será cierta si el F calculado cumple: 0,406≤Fc≤2,46. De lo contrario se rechaza la hipótesis nula.
Como Fc=(2,13/1,96)^2 = 1,18 se concluye que el estadístico Fc está en el rango de aceptación de la hipótesis nula con una certeza del 95%. En otras palabras con una certeza del 95% ambos procesos de manufactura tienen la misma varianza poblacional.
- F Test for Independence. Recuperado de: saylordotorg.github.io.
- Med Wave. Estadística aplicada a las ciencias de la salud: la prueba F. Recuperado de: medwave.cl.
- Probabilidades y Estadística. Distribución F. Recuperado de: probabilidadesyestadistica.com.
- Triola, M. 2012. Elementary Statistics. 11th. Edition. Addison Wesley.
- UNAM. Distribución F. Recuperado de: asesorias.cuautitlan2.unam.mx.
- Wikipedia. Distribución F. Recuperado de: es.wikipedia.com
