Método Trachtenberg: en qué consiste, ejemplos
El método Trachtenberg es un sistema para realizar operaciones aritméticas, principalmente la multiplicación, de una forma fácil y rápida, una vez conocidas y dominadas sus reglas.
Fue ideado por el ingeniero de origen ruso Jakow Trachtenberg (1888-1953) cuando estaba prisionero de los nazis en un campo de concentración, como una forma de distracción para mantener la cordura mientras continuaba en cautiverio.
Índice del artículo
- 1 En qué consiste, ventajas y desventajas
- 2 Ejemplos
- 3 Reglas para los productos por 6, 7 y 5
- 4 Reglas para los productos por 9
- 5 Multiplicación por 8, 4, 3 y 2
- 6 Multiplicar por cifras compuestas
- 7 Referencias
La ventaja que representa este método radica en que para realizar multiplicaciones no es necesario memorizar las tablas de multiplicar, al menos en parte, solamente basta con saber contar y sumar, así como dividir entre dos un dígito.
La desventaja es que no hay una regla universal para multiplicar por cualquier cifra, sino que la regla varía de acuerdo al multiplicador. Sin embargo, los patrones no son difíciles de memorizar y en principio permiten realizar operaciones sin ayuda de papel y lápiz.
A lo largo de este artículo nos concentraremos en las reglas para multiplicar rápidamente.
Para aplicar el método es preciso conocer las reglas, por eso vamos a presentarlas una a una y con ejemplos:
Regla para multiplicar por 10
-Para multiplicar cualquier cifra por 10, simplemente se agrega un cero a la derecha. Por ejemplo: 52 x 10 = 520.
Reglas para multiplicar por 11
-Se agrega al inicio y al final de la cifra un cero.
-Se suma cada dígito con su vecino de la derecha y el resultado se coloca debajo del dígito correspondiente de la cifra original.
-Si el resultado sobrepasa nueve, entonces se anota la unidad y se le coloca un puntito para recordar que llevamos una unidad que se agregara en la suma de la próxima cifra con su vecino de la derecha.
Ejemplo detallado de multiplicación por 11
Multiplicar 673179 por 11
06731790 x 11=
————-
= 7404969
Los pasos necesarios para llegar a este resultado, ilustrados mediante colores, son los siguientes:
-Se multiplicó el 1 de la unidad del multiplicador (11) por el 9 del multiplicando (06731790) y se le agregó 0. Se obtuvo el dígito de la unidad del resultado: 9.
-Luego se multiplica 1 por 7 y se le suma nueve da 16 y llevamos 1, se coloca el dígito de la decena: 6.
-Después se multiplica 1 por 1 se le suma el vecino de la derecha 7 más 1 que llevaba da como resultado 9 para la centena.
-La próxima cifra se obtiene de multiplicar 1 por 3 más el vecino 1, resulta 4 para el dígito de los miles.
-Se multiplica 1 por 7 y se le suma el vecino 3 resultando 10, se coloca el cero (0) como dígito de los diezmiles y se lleva uno.
-Luego 1 por 6 más el vecino 7 resulta 13 más un 1 que llevaba resulta 14, se coloca el 4 como dígito de los cien-miles y se lleva 1.
-Finalmente se multiplica 1 por el cero que se agregó al comienzo, dando cero más el vecino 6 más uno que se llevaba. Resulta finalmente 7 para el dígito correspondiente a los millones.
Para multiplicar por 12 cualquier cifra:
-Se agrega un cero al inicio y otro cero al final de la cifra a multiplicar.
-Se duplica cada dígito de la cifra a multiplicar y se suma con su vecino de la derecha.
-Si la suma sobrepasa 10 se agrega una unidad a la próxima operación de duplicación y suma con el vecino.
Ejemplo de multiplicación por 12
Multiplicar 63247 por 12
0632470 x 12 =
———–
758964
Los detalles para llegar a este resultado, siguiendo estrictamente las reglas enunciadas, se muestran en la siguiente figura:

El método de multiplicación por 12 puede extenderse a las multiplicaciones por 13, 14 hasta el 19 simplemente cambiando la regla de duplicar por triplicar para el caso del trece, cuadruplicar para el caso del 14 y así sucesivamente hasta llegar al 19.
-Agregar ceros al inicio y final de la cifra a multiplicar por 6.
-Sumar a cada dígito la mitad de su vecino de la derecha, pero si el dígito es impar sumar 5 adicionalmente.
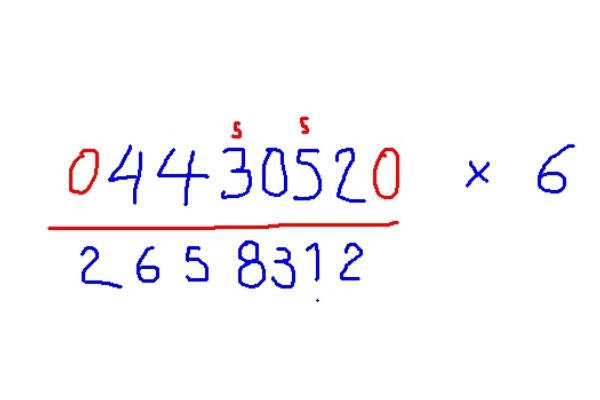
-Agregar ceros al inicio y al final de la cifra a multiplicar.
-Duplicar cada dígito y sumar la mitad entera inferior del vecino, pero si el dígito es impar adicionalmente sumar 5.
Ejemplo de multiplicación por 7
-Multiplicar 3412 por 7
-El resultado es 23884. Para aplicar las reglas es recomendable en primer lugar reconocer los dígitos impares y colocarles encima un pequeño 5 para recordar sumar esta cifra al resultado.
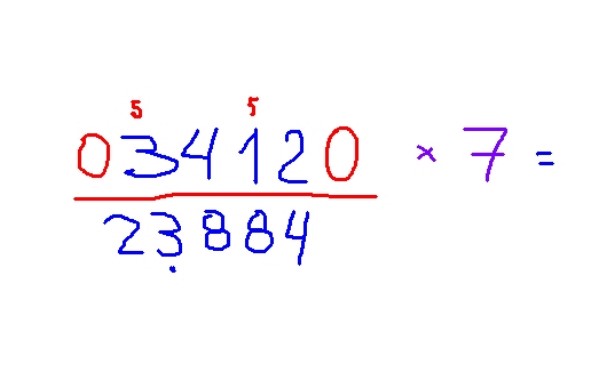
-Agregar ceros al inicio y al final de la cifra a multiplicar.
-Colocar debajo de cada dígito la mitad entera inferior del vecino de la derecha, pero si el dígito es impar sumar adicionalmente 5.
Ejemplo de multiplicación por 5
Multiplicar 256413 por 5
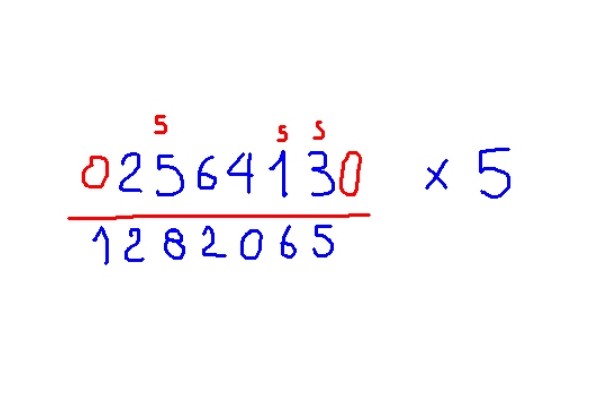
-Se agrega un cero al inicio y otro al final de la cifra a multiplicar por nueve.
-El primer dígito a la derecha se obtiene de restar a 10 el dígito correspondiente de la cifra a multiplicar.
-Luego se le resta a 9 el dígito siguiente y se le suma el vecino.
-Se repite el paso anterior hasta llegar al cero del multiplicando, donde restamos 1 al vecino y el resultado se copia debajo del cero.
Ejemplo de multiplicación por 9
Multiplicar 8769 por 9:
087690 x 9 =
————-
78921
Operaciones
10 – 9 = 1
(9-6) + 9 =12 (se copia el 2 y se lleva 1)
(9-7)+1+6=9
(9-8)+7 =8
(8-1) = 7
-Agregar ceros al inicio y al final de la cifra a multiplicar.
-Para el primer dígito de la derecha restar de 10 y el resultado se duplica.
-Para los siguientes dígitos restar de 9, el resultado se duplica y se le suma el vecino.
-Al llegar al cero restar 2 al vecino de la derecha.
Ejemplo de multiplicación por 8
-Multiplicar 789 por 8
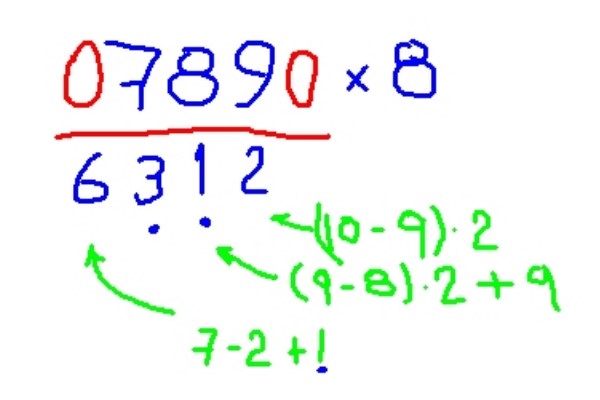
-Agregar ceros a la derecha e izquierda del multiplicando.
-Restar de 10 el dígito correspondiente de la unidad agregando 5 si se trata de un dígito impar.
-Restar de 9 en forma cada dígito del multiplicando, agregando la mitad del vecino de la derecha y si se trata de un dígito impar sumar 5 adicionalmente.
-Al llegar al cero del comienzo del multiplicando colocar la mitad del vecino menos uno.
Ejemplo de multiplicación por 4
Multiplicar 365187 x 4
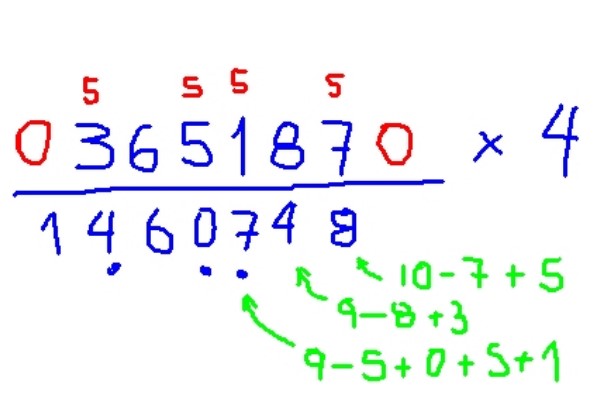
-Agregar cero a cada extremo del multiplicando.
-Restar 10 menos el dígito de la unidad y agregar 5 si es un dígito impar.
-Para los otros dígitos, restarle a 9 duplicar el resultado, sumar la mitad del vecino y sumar 5 si es impar.
-Al llegar al cero de la cabecera colocar la mitad entera menor del vecino menos 2.
Ejemplo de multiplicación por 3
Multiplicar 2588 por 3

-Agregar ceros en los extremos y duplicar cada dígito, si sobrepasa 10 sumar uno al siguiente.
Ejemplo de multiplicación por 2
Multiplicar 2374 por 2
023740 x 2
04748
Se aplican las reglas enunciadas anteriormente, pero los resultados se van corriendo a la izquierda el número de lugares correspondientes a decenas, centenas y así sucesivamente. Veamos el siguiente ejemplo:
Multiplicar 37654 por 498
0376540 x 498
301232 regla para 8
338886 regla para 9
150616 regla para 4
18751692 suma final
- Cutler, Ann. 1960.The Trachtenberg speed system of basic mathematics. Doubleday & CO, NY.
- Dialnet. Sistema rápido de matemática básica. Recuperado de: dialnet.com
- Rincón matemático. Multiplicación rápida por el método de Trachtenberg. Recuperado de: rinconmatematico.com
- The Trachtenberg Speed System of Basic Mathematics. Recuperado de: trachtenbergspeedmath.com
- Wikipedia. Método Trachtenberg. Recuperado de: wikipedia.com
