Efecto Doppler: descripción, fórmulas, casos, ejemplos
El efecto Doppler es un fenómeno físico que se produce cuando el receptor y la fuente de ondas tienen movimiento relativo, causando un cambio en la frecuencia del receptor respecto a la frecuencia de la fuente.
Su nombre se debe al físico austriaco Christian Doppler (1803-1853), quien describió y explicó este fenómeno en 1842, mientras presentaba un trabajo sobre el color de las estrellas dobles, en un congreso de ciencias naturales en Praga, actual República Checa.

Índice del artículo
- 1 ¿Dónde se presenta el efecto Doppler?
- 2 Descripción del efecto Doppler
- 3 Fórmulas
- 4 Casos en los que existe el efecto Doppler
- 5 Ejemplos de efecto Doppler
- 6 Aplicaciones
- 7 Ejercicios
- 8 Referencias

El efecto Doppler se presenta en todo tipo de ondas, desde las luminosas hasta las sonoras, siempre que la fuente y el receptor se estén moviendo el uno respecto del otro. Y es mucho más notable cuando la velocidad relativa entre la fuente y receptor es comparable a la velocidad de propagación de la onda.
Supóngase una onda armónica, que es una oscilación que avanza en el espacio. La oscilación se repite a intervalos de tiempo regulares, este tiempo es el período y su inverso la frecuencia, es decir el número de oscilaciones por unidad de tiempo.
Cuando la distancia entre la fuente de la onda armónica y el receptor permanece fija, el receptor percibe la misma frecuencia de la fuente, es decir, registra el mismo número de pulsos por unidad de tiempo que la fuente.
Sin embargo, cuando el receptor se va acercando a la fuente con rapidez fija, entonces los pulsos le van llegando con mayor frecuencia. Y lo contrario ocurre cuando el receptor se aleja a rapidez fija de la fuente: los pulsos de onda se perciben con una frecuencia menor.

Para entender porqué ocurre este fenómeno usaremos una analogía: dos personas jugando a lanzar bolas. El lanzador las hace rodar en línea recta sobre el suelo hacia el compañero, que las recoge.
Si la persona que lanza envía una bola cada segundo, el que las recoge, si se mantiene fijo, atrapará una bola cada segundo. Todo bien hasta ahora, ya que es lo esperado.
Ahora supongamos que la persona que atrapa las bolas está sobre una patineta y decide acercarse al lanzador con rapidez constante. En este caso, como va al encuentro de las bolas, tendrá menos de un segundo entre una bola y la siguiente.
Por lo tanto, al receptor le parece que le llega más de una bola por segundo, es decir, aumentó la frecuencia con la que llegan a su mano.
Lo contrario ocurriría si persona receptora decidiera alejarse del emisor, es decir, el tiempo de llegada de las bolas aumentaría con la consecuente disminución de frecuencia con la que le llegan las bolas.
El cambio de frecuencia descrito en el apartado anterior puede obtenerse a partir de la siguiente fórmula:
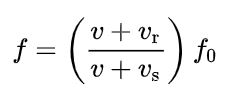
Aquí:
-fo es la frecuencia de la fuente.
-f es la frecuencia aparente en el receptor.
-v es la rapidez (v > 0) de propagación de la onda en el medio.
-vr es la velocidad del receptor respecto al medio y
-vs es la velocidad de la fuente relativa al medio.
Nótese que vr es positiva si el receptor se acerca a la fuente y negativa en caso contrario. Por otra parte, vs es positiva si la fuente se aleja del receptor y negativa cuando se acerca.
En definitiva, si la fuente y el observador se acercan, la frecuencia aumenta y si se alejan disminuye. Lo contrario ocurre con la longitud de onda aparente en el receptor (ver ejercicio 1).
Frecuentemente ocurre que la rapidez de la onda es muchísimo mayor que la rapidez con la que se mueve la fuente o la rapidez de movimiento del receptor.
En este caso la fórmula puede aproximarse de modo tal que quede escrita en función de la velocidad relativa del receptor (observador) respecto de la fuente (s).
En este caso la fórmula sería así:
f = [1 + (Vrs/v)]⋅fo
Donde Vrs = vr – vs.
Cuando Vrs es positiva (se acercan), la frecuencia f es mayor que fo, mientras que cuando es negativa (se alejan), f es menor que fo.
La fórmula anterior aplica únicamente para el caso que la fuente se acerque (o se aleje) directamente del observador.
En caso que la fuente se mueva en siguiendo un camino transversal, se necesita tomar en cuenta el ángulo θ que forma la velocidad relativa del receptor -respecto de la fuente- con la dirección del vector que va del observador a la fuente.
En tal caso debemos aplicar:
f = [1 + (Vrs ⋅ Cos(θ) / v)] ⋅ fo
De nuevo, a Vrs se le asigna signo positivo si el receptor y la fuente se están acercando, y negativo si ocurre al contrario.
Un ejemplo cotidiano es la sirena de una ambulancia o patrulla. Cuando se acerca hacia nosotros se percibe más aguda y cuando se aleja es más grave, particularmente se escucha la diferencia en el momento de máximo acercamiento.
Otra situación que se explica mediante el efecto Doppler es el corrimiento de las líneas espectrales de las estrellas hacia el azul o el rojo, si se están acercando hacia nosotros o si se están alejando. Esto no puede notarse a simple vista, pero si con un instrumento llamado espectrómetro.
El efecto Doppler tiene muchas aplicaciones prácticas, a continuación se enumeran algunas:
Los radares miden la distancia y la velocidad a la que se desplazan los objetos detectados por el mismo y se basan justamente en el efecto Doppler.
El radar emite una onda hacia el objeto que se quiere detectar, luego esa onda se refleja de vuelta. El tiempo que tarda un pulso en ir y volver sirve para determinar la distancia a la que se encuentra el objeto. Y el cambio de frecuencia en la señal reflejada permite saber si el objeto en cuestión se aleja o se acerca al radar y con qué rapidez.
Debido a que la onda de radar va y vuelve, se produce un doble efecto Doppler. En tal caso, la fórmula que permite determinar la rapidez del objeto respecto del radar es:
Vo/r = ½ c ⋅ (Δf / fo)
Donde:
-Vo/r es la velocidad del objeto respecto del radar.
-c la rapidez de la onda emitida y luego reflejada.
-fo la frecuencia de emisión en el radar.
-Δf el corrimiento de frecuencia, es decir f – fo.
Gracias al efecto Doppler se ha podido determinar que el universo está en expansión, ya que el espectro luminoso que emiten las galaxias lejanas está desplazado hacia el rojo (una disminución de frecuencia).
Por otra parte, también se sabe que la rapidez de alejamiento crece en la medida que las galaxias observadas son más distantes.
Caso contrario ocurre con algunas galaxias del grupo local, es decir las vecinas de nuestra Vía Láctea.
Por ejemplo, nuestra vecina más cercana, la galaxia de Andrómeda tiene un corrimiento hacia el azul (es decir un aumento de frecuencia) lo que indica que se nos está acercando.
Es una variante del ecosonograma tradicional, en la que aprovechando el efecto Doppler se mide la velocidad del flujo sanguíneo en venas y arterias.
La sirena de una ambulancia tiene una frecuencia es de 300 Hz. Sabiendo que la velocidad del sonido en el aire es 340 m/s, determine la longitud de onda del sonido en los siguientes casos:
a) Cuando la ambulancia está en reposo.
b) Si se acerca a 108 km/h
c) Al alejarse a la misma rapidez.
Solución a
No hay efecto Doppler porque tanto el emisor como la fuente están en reposo.
Para determinar la longitud de onda del sonido se usa la relación entre la frecuencia de la fuente f, la longitud de onda λ de la fuente y la velocidad del sonido v:
v = fo⋅λ.
De allí se deduce que:
λ = v / fo.
Por lo tanto la longitud de onda es:
λ = (340 m/s) / (300 1/s) = 1,13 m.
Solución b
El receptor se considera en reposo, es decir que vr = 0. El emisor es la sirena que se mueve con la rapidez de la ambulancia:
vs = (108/3,6)m/s = 30 m/s.
La frecuencia aparente f viene dada por la relación:
f = fo⋅ [(v + vr)/(v + vs)]
Aplicando esta fórmula se obtiene:
f = 300 Hz ⋅ [(340 + 0)/(340 – 30)] = 329 Hz.
La longitud de onda en el receptor será:
λr= v / f = (340 m/s) / (329 1/s) = 1,03 m.
Solución c
Se resuelve de manera similar:
f = 300 Hz ⋅(340 + 0)/(340 + 30) = 276 Hz.
La longitud de onda en el receptor será:
λr = v / f = (340 m/s) / (276 1/s) = 1,23 m.
Se concluye que los frentes de onda tienen una separación de 1,03 m cuando la sirena se acerca y de 1,23 m cuando se aleja.
Una línea característica del espectro de emisión del hidrógeno está a 656 nm, pero al observar una galaxia se ve que esa misma línea está desplazada y marca 660 nm, es decir tiene un corrimiento hacia el rojo de 4 nm.
Como hay un aumento de la longitud de onda, sabemos que la galaxia se aleja. ¿Cuál es su velocidad?
Solución
El cociente entre el desplazamiento de la longitud de onda y la longitud de onda en reposo es igual al cociente entre la velocidad de la galaxia y la velocidad de la luz (300.000 km/s). Entonces:
4/656= 0.006
Por lo tanto la galaxia se aleja a 0.006 veces la velocidad de la luz, es decir a 1800 km/s.
- Alonso – Finn. Física vol.2. 1970. Fondo educativo interamericano, S.A.
- Baranek, L. 1969. Acústica. 2da. Edición. McGraw Hill.
- Griffiths G. Linear and Nonlinear Waves. Recuperado de: scholarpedia.org.
- Whitham G.B. 1999. Linear and Nonlinear Waves. Wiley.
- Wikiwaves. Nonlinear waves. Recuperado de: wikiwaves.org
- Wikipedia. Efecto Doppler. Recuperado de: es.wikipedia.com
