Diferencias entre velocidad y rapidez (con ejemplos)

Las diferencias entre velocidad y rapidez existen, pese a que ambas son cantidades físicas relacionadas. En el lenguaje común se usa indistintamente un término o el otro como si fuesen sinónimos, pero en Física es preciso distinguirlos.

En este artículo se definen ambos conceptos, se señalan las diferencias y se explica, mediante ejemplos, cómo y cuándo se aplica uno u otro. Para simplificar consideramos una partícula en movimiento y a partir de allí revisaremos los conceptos de velocidad y rapidez. 

Ejemplos con rapidez uniforme sobre tramos rectos

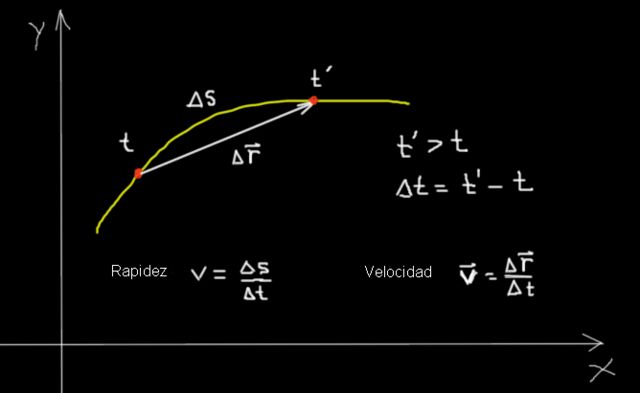
En la tabla anterior se resumieron varios aspectos de la rapidez y la velocidad. Y a continuación, para complementar, se consideran varios ejemplos que ilustran los conceptos involucrados y sus relaciones:

– Ejemplo 1

Suponga que una hormiga roja se mueve siguiendo una línea recta y en la dirección indicada en la figura siguiente.

Además, la hormiga se mueve de forma uniforme de modo tal que recorre una distancia de 30 milímetros en un  lapso de tiempo de 0,25 segundos. 

Determine la  rapidez y velocidad la de la hormiga.

Solución 

La rapidez de la hormiga se calcula dividiendo la distancia Δs recorrida entre el lapso de tiempo Δt.

v = Δs/Δt = (30 mm)/(0,25s) = 120 mm/s = 12 cm/s

La velocidad de la hormiga se calcula dividiendo el desplazamiento Δr entre el lapso de tiempo en el que se efectuó dicho desplazamiento.

El desplazamiento fue de 30 mm en dirección 30º respecto del eje X, o en forma compacta: 

Δr = (30 mm ¦ 30º)

Puede notarse que el desplazamiento consta de una magnitud y una dirección, ya que se trata de una cantidad vectorial. Alternativamente el desplazamiento puede expresarse según sus componentes cartesianas X e Y, de esta manera:

Δr = (30 mm* cos(30º) ; 30 mm* sin(30º) ) = (25,98 mm ; 15,00 mm)

La velocidad de la hormiga se calcula dividiendo el desplazamiento entre el lapso de tiempo en el que se efectuó:

v = Δr/Δt = (25,98 mm / 0,25 s ; 15,00 mm / 0,25 s) = (103,92 ; 60,00) mm/s

Esta velocidad en componentes cartesianas X e Y y en unidades de cm/s es:

v = (10,392 ; 6,000) cm/s.

Alternativamente el vector velocidad puede ser expresado en su forma polar (módulo ¦ dirección) como se muestra:

v = (12 cm/s ¦ 30º).

Nota: en este ejemplo como la velocidad es constante coinciden la velocidad media y la velocidad instantánea. Se comprueba que el módulo de la velocidad instantánea es la rapidez instantánea.

Ejemplo 2

La misma hormiga del ejemplo anterior va desde A hasta B, luego de B hacia C y por último de C hacia A, siguiendo el camino triangular mostrado en la figura siguiente.

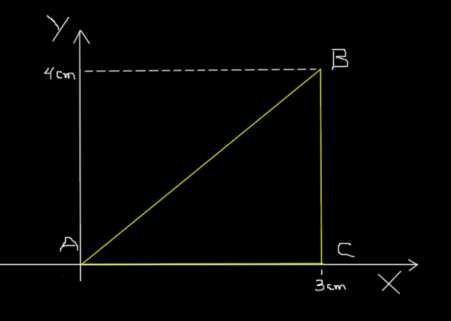
El tramo AB lo recorre en 0,2s; el BC lo recorre en 0,1s y finalmente CA lo recorre en 0,3s. Calcule la rapidez media del recorrido ABCA y la velocidad media del recorrido ABCA.

Solución 

Para calcular la rapidez media de la hormiga, comenzamos por determinar la distancia total recorrida:

Δs = 5 cm + 4 cm + 3 cm = 12 cm.

El lapso de tiempo empleado para todo el trayecto es:

Δt = 0,2s + 0,1s + 0,3s = 0,6 s.

Entonces, la rapidez media de la hormiga es:

v = Δs/Δt = (12 cm)/(0,6s) = 20 cm/s.

Seguidamente se calcula la velocidad media de la hormiga en el recorrido ABCA. En este caso, el desplazamiento efectuado por la hormiga es:

Δr = (0 cm; 0 cm)

Esto se debe a que el desplazamiento es la diferencia entre la posición final menos la posición inicial. Como ambas posiciones son la mismas, entonces su diferencia es nula, resultando un desplazamiento nulo.

Este desplazamiento nulo se efectuó en un lapso de tiempo de 0,6s por lo que la velocidad media de la hormiga fue:

v =(0 cm; 0 cm)/ 0,6s = (0 ; 0) cm/s.

Conclusión: rapidez media 20 cm/s, pero la velocidad media es nula en el recorrido ABCA.

Ejemplos con rapidez uniforme sobre tramos curvos

Ejemplo 3

Un insecto se mueve sobre un círculo de 0,2m de radio con rapidez uniforme, de modo tal que partiendo de A y llegando a B, recorre ¼ de circunferencia en 0,25 s.

Determine la rapidez  y la velocidad del insecto en el tramo AB.

Solución 

La longitud del arco de circunferencia comprendido entre A y B es:

Δs = 2πR /4 = 2π(0,2m)/4 = 0,32 m.

Aplicando la definición de rapidez media se tiene:

v = Δs/Δt = 0,32 m / 0,25 s = 1,28 m/s.

Para calcular la velocidad media, se requiere calcular el vector desplazamiento entre la posición inicial A y la final B:

Δr = (0 ; R) – (R ; 0) = (-R ; R) = (-0,2 ; 0,2)m

Aplicando la definición de velocidad media se obtiene:

v = Δr/Δt = (-0,2 ; 0,2)m / 0,25s = (-0.8 ; 0,8) m/s.

La expresión anterior es la velocidad media entre A y B expresada en forma cartesiana. Alternativamente la velocidad media puede ser expresada en forma polar, es decir módulo y dirección:

| v | = ( (-0,8)^2 + 0,8^2 )^(½) = 1,13 m/s

Dirección = arctan ( 0,8 / (-0,8) ) = arctan(-1) = -45º + 180º =135º respecto al eje X.

Finalmente, el vector velocidad media en forma polar es: v =(1,13 m/s ¦ 135º).

Ejemplo 4

Suponiendo que el instante de partida del insecto del ejemplo anterior es 0s desde el punto A, se tiene que su vector posición en un instante cualquiera t está dado por:

r(t) = [ R cos((π/2) t) ;  R sen((π/2) t) ].

Determine la velocidad y la rapidez instantánea para cualquier instante t.

Solución 

La velocidad instantánea es la derivada respecto del tiempo de la función posición:

v(t) = dr/dt =  [ -R (π/2) sin((π/2) t) ;  R (π/2) cos((π/2) t) ]

La rapidez instantánea es el módulo del vector velocidad instantánea:

v(t) = | v(t) | = π R / 2^½

Referencias

1. Alonso M., Finn E. Física volumen I: Mecánica. 1970. Fondo Educativo Interamericano S.A.
2. Hewitt, P. Conceptual Physical Science. Fifth edition. Pearson.
3. Young, Hugh. University Physics with Modern Physics. 14th Ed. Pearson.
4. Wikipedia. Velocidad. Recuperado de: es.wikipedia.com
5. Zita, A. Diferencia entre velocidad y  rapidez. Recuperado de: diferenciador.com