Divisiones en las que el residuo sea 300
Existen muchas divisiones en las que el residuo sea 300. Además de citar algunas de ellas, se mostrará una técnica que ayuda a construir cada una de estas divisiones, la cual no depende del número 300.
Esta técnica es proporcionada por el algoritmo de la división de Euclides, que establece lo siguiente: dados dos números enteros “n” y “b”, con “b” diferente de cero (b≠0), existen únicos enteros “q” y “r”, tales que n=bq+r, donde 0 ≤ “r” |b|.
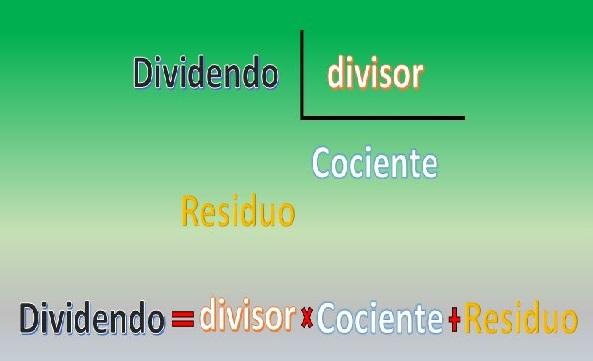
Los números “n”, “b”, “q” y “r” son llamados dividendo, divisor, cociente y residuo (o resto), respectivamente.
Cabe destacar que al exigir que el residuo sea 300, implícitamente se está diciendo que el valor absoluto del divisor debe ser mayor estricto que 300, es decir: |b|>300.
Ejemplos de divisiones en las que el residuo sea 300
A continuación se presentan algunas divisiones en las que el residuo es 300; luego, se presenta el método de construcción de cada división.
1- 1000÷350
Si se divide 1000 entre 350, se puede apreciar que el cociente es 2 y el residuo es 300.
2- 1500÷400
Al dividir 1500 entre 400, se obtiene que el cociente es 3 y el residuo es 300.
3- 3800÷700
Al efectuar esta división resultará que el cociente es 5 y el residuo será 300.
4- 1350÷(−350)
Cuando se resuelve esta división se obtiene -3 como cociente y 300 como residuo.
¿Cómo se construyen estas divisiones?
Para construir las divisiones anteriores solo hace falta usar de manera adecuada el algoritmo de la división.
Los cuatro pasos para construir estas divisiones son:
1- Fijar el residuo
Como se quiere que el residuo sea 300, se fija r=300.
2- Escoger un divisor
Ya que el residuo es 300, el divisor que se vaya a escoger debe ser cualquier número tal que su valor absoluto sea mayor que 300.
3- Escoger un cociente
Para el cociente se puede escoger cualquier número entero diferente de cero (q≠0).
4- Se calcula el dividendo
Una vez fijados el residuo, el divisor y el cociente, se sustituyen en el lado derecho del algoritmo de la división. El resultado será el número que se debe escoger como dividendo.
Con estos cuatro sencillos pasos se puede apreciar cómo se construyó cada división de la lista de arriba. En todas éstas se fijó r=300.
Para la primera división se escogieron b=350 y q=2. Al sustituir en el algoritmo de la división se obtuvo como resultado 1000. De modo que el dividendo debe ser 1000.
Para la segunda división se establecieron b=400 y q=3, de modo que al sustituir en el algoritmo de la división se obtuvo 1500. Así se establece que el dividendo es 1500.
Para la tercera se escogió como divisor el número 700 y como cociente el número 5. Al evaluar estos valores en el algoritmo de la división se obtuvo que el dividendo debe ser igual a 3800.
Para la cuarta división se fijaron el divisor igual a -350 y el cociente igual a -3. Cuando se sustituyen estos valores en el algoritmo de la división y se resuelve, se obtiene que el dividendo es igual a 1350.
Siguiendo estos pasos se pueden construir muchas más divisiones en las que el residuo es 300, teniendo cuidado cuando se quieran usar números negativos.
Se debe notar que el proceso de construcción descrito arriba se puede aplicar para construir divisiones con residuos diferentes a 300. Solo se cambia el número 300, en el primer y segundo paso, por el número deseado.
