Ecuación general de la parábola (ejemplos y ejercicios)
La ecuación general de la parábola contiene términos cuadráticos en x y en y, así como términos lineales en ambas variables más un término independiente. El eje de simetría de la primera es paralelo al eje vertical y el de la segunda lo es al eje horizontal.
En general, la ecuación cuadrática que carece del término cruzado xy se escribe como:
Ax2 + Cy2 +Dx + Ey + F = 0
Los valores de A, C, D, E y F son números reales. Imponiendo las condiciones A∙C = 0 y A+C≠0, la curva que resulta de graficar los puntos que satisfacen dicha ecuación es una parábola.
Caso 1
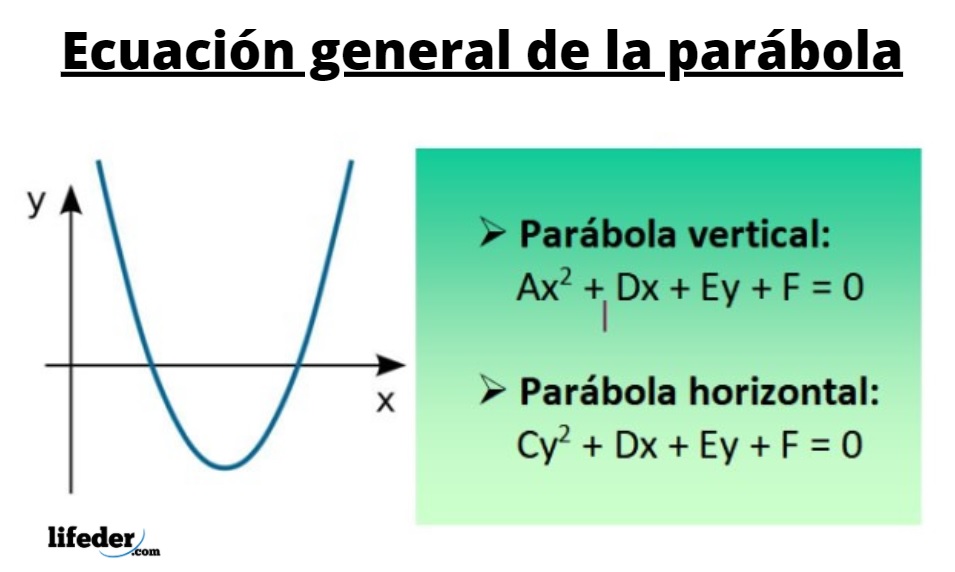
Para una parábola vertical, su ecuación general es:
Ax2 + Dx + Ey + F = 0
Donde A y E son diferentes de 0. En otras palabras, cuando aparece un término con x2, la parábola es vertical.
Caso 2
Por su parte, para la parábola horizontal se tiene:
Cy2 + Dx + Ey + F = 0
Aquí C y D son también son distintos de 0, por lo tanto el término cuadrático corresponde a y2.
En todo caso, la ecuación general de la parábola es cuadrática en una de las variables y lineal en la otra.
Elementos de la parábola
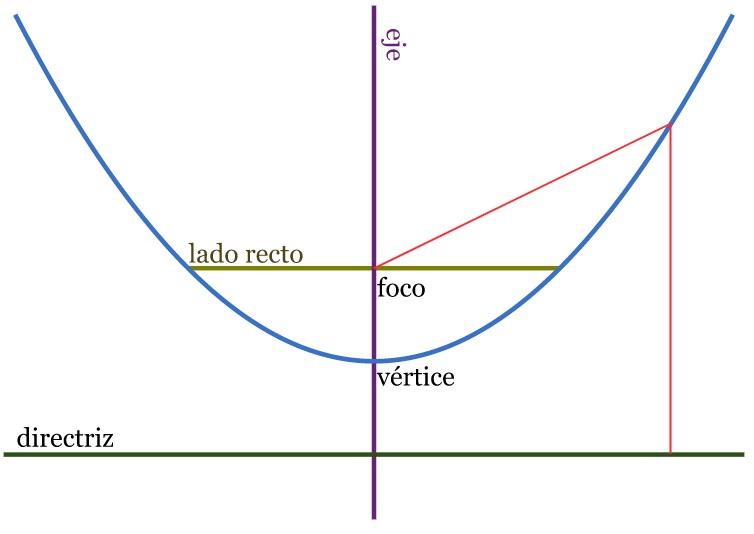
La parábola, definida como lugar geométrico, consiste en el conjunto de puntos de un plano que equidistan de otro punto llamado foco y también de una recta, conocida como recta directriz.
A partir de la ecuación general, es posible hacer el estudio de la parábola al especificar sus elementos. Incluyendo al foco y a la recta directriz, dichos elementos, descritos brevemente son:
–Eje, que se refiere al eje de simetría de la parábola, puede ser horizontal (paralelo al eje de las abscisas) o vertical (paralelo al eje de las ordenadas).
–Orientación, que a su vez corresponde a la orientación del eje. La parábola es vertical si su eje de simetría es vertical, y es horizontal cuando el eje también lo es.
–Vértice, es el punto en el cual el eje intersecta a la parábola.
–Foco, punto ubicado sobre el eje, por dentro de la parábola y a una distancia p del vértice. Todos los puntos de la parábola equidistan del foco y de la recta directriz.
–Parámetro, es la distancia p entre el foco y el vértice.
–Recta directriz, la cual es perpendicular al eje y también dista una distancia p del vértice de la parábola, pero no interseca a esta, ya que está por fuera.
–Lado recto, es la cuerda que pasa por el foco, intersectando a la parábola en dos puntos, perpendicularmente a su eje.
–Excentricidad, que en el caso de la parábola siempre vale 1.
–Representación gráfica.
La información para determinar todos estos elementos se encuentra contenida en la ecuación general.
La forma canónica
Para determinar los elementos de la parábola a veces es conveniente pasar de la forma general a la forma canónica de la misma, mediante el método de completar cuadrados en la variable cuadrática.
Dicha forma canónica es:
(x-h)2 = 4p(y–k)
Donde el punto (h,k) es el vértice V de la parábola. Igualmente puede convertirse la forma canónica a la ecuación general, desarrollando el producto notable y reordenando los términos.
Ejemplos
Ejemplo 1
Las siguientes son ecuaciones de la parábola en forma general:
a) 4x2 + 5y – 3 = 0
b) 1 – 2y + 3x –y2 = 0
En a) se identifican los coeficientes: A = 4, C = 0, D = 0, E = 5, F = -3. Se trata de una parábola cuyo eje de simetría es vertical.
Por su parte, en b) la ecuación general queda:
– y2 + 3x – 2y + 1= 0
Y los coeficientes son: C = –1, D = 3, E = -2 y F = 1.
Ejemplo 2
La siguiente parábola está en forma canónica:
(y–1)2 = 6(x–3)
Para encontrar su ecuación general primero se desarrolla el producto notable y se efectúa el paréntesis a la derecha:
y2 –2y + 1 = 6x –18
Ahora se pasan todos los términos a la izquierda y se agrupan convenientemente:
y2 –2y + 1– 6x +18 = 0 → y2 – 6x –2y + 19 = 0
Como el término cuadrático es y2 se trata de una parábola horizontal. Los coeficientes son:
C=1; D= –6; E = –2, F = 19.
Ejercicios resueltos
Ejercicio 1
La parábola siguiente está dada en forma general:
x2 –10x–12y – 11 = 0
Se pide escribirla en la forma canónica.
Solución
Pasar a la forma canónica se logra completando cuadrados, en este caso, en la variable x. Se comienza escribiendo entre paréntesis los términos en x:
(x2 –10x) –12y – 11 = 0
Hay que transformar lo que está entre paréntesis en un trinomio cuadrado perfecto, lo cual se consigue sumando 52, que naturalmente se tiene que restar, porque de lo contrario se altera la expresión. Queda así:
(x2 −10x+52) −12y – 11−52= 0
Los tres términos entre paréntesis constituyen el trinomio cuadrado perfecto (x-5)2. Se puede comprobar desarrollando este producto notable para corroborar. Ahora la parábola queda:
(x–5)2 –12y –36 = 0
Lo que sigue es factorizar los términos fuera del paréntesis:
(x–5)2 –12(y +3) = 0
Que se transforma finalmente en:
(x–5)2 =12(y +3)
Ejemplo 2
Hallar los elementos de la parábola anterior y construir su gráfica.
Solución
Vértice
El vértice de la parábola tiene coordenadas V (5, -3)
Eje
La recta x = 5.
Parámetro
En cuanto al valor del parámetro p que aparece en la forma canónica: (x–h)2 = 4p(y–k) se encuentra comparando ambas ecuaciones:
4p = 12
p = 12/4 = 3
Orientación
Esta parábola es vertical y abre hacia arriba. Como el vértice está ubicado en x = 5, y = -3, entonces el eje de simetría es la recta vertical x = 5.
Foco
El foco está sobre la recta x = 5, por lo tanto tiene coordenada x = 5 también.
La coordenada y del foco debe estar p unidades por encima de k, es decir: p + k = 3 + (-3) = 0, luego el foco está en el punto (5,0).
Recta directriz
Es perpendicular al eje, por lo tanto es de la forma y = c, ahora bien, como dista una distancia p del vértice, pero fuera de la parábola, quiere decir que está a una distancia p por debajo de k:
y = k – p = -3-3 = -6
Lado recto
Este segmento corta a la parábola, pasa por el foco y es paralelo a la recta directriz, por lo tanto está contenido en la recta y = 0.
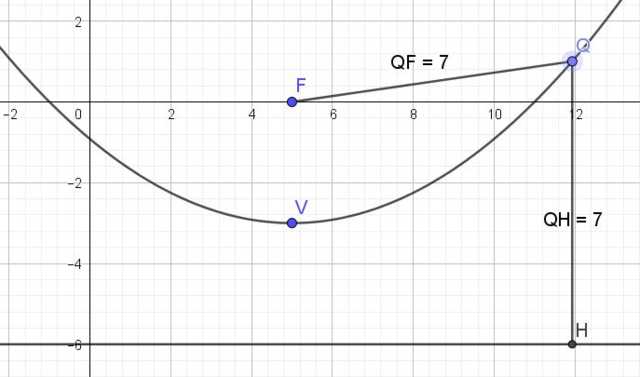
Representación gráfica
Se puede obtener fácilmente a partir de un software de graficación online gratuito, como por ejemplo Geogebra. En la casilla de entrada se coloca así:
Referencias
- Baldor. 1977. Álgebra Elemental. Ediciones Cultural Venezolana.
- Hoffman, J. Selección de temas de Matemática. Volumen 2.
- Jiménez, R. 2008. Álgebra. Prentice Hall.
- Stewart, J. 2006. Precálculo: Matemáticas para el Cálculo. 5ta. Edición. Cengage Learning.
- Zill, D. 1984. Álgebra y Trigonometría. McGraw Hill.
