Clasificación de los Números Reales
La principal clasificación de los números reales se divide en los números naturales, los números enteros, los números racionales y los números irracionales. Los números reales son representados con la letra R.
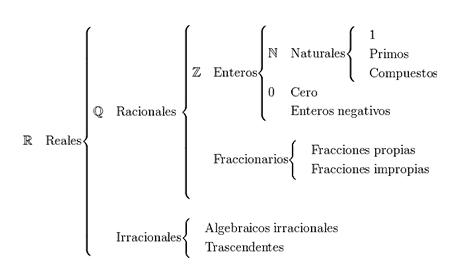
Hay muchas maneras en las que los distintos números reales pueden ser construidos o descritos, variando desde unas formas más sencillas hasta unas más complejas, dependiendo del trabajo matemático que se quiere realizar.
¿Cómo se clasifican los números reales?
– Números naturales
Los números naturales están representados por la letra (n) y son aquellos que se utilizan para contar (0,1,2,3,4…). Por ejemplo “hay quince rosas en el jardín”, “La población de México es de 126millones de personas” o “La suma de dos y dos es cuatro“. Habría que reseñar que algunas clasificaciones incluyen al 0 como número natural y otras no.

Los números naturales no incluyen aquellos que tienen parte decimal. Por lo tanto, “La población de México es de 126,2 millones de personas” o “Hace una temperatura de 24,5 grados centígrados” no podrían considerarse números naturales.
En el lenguaje común, como por ejemplo en las escuelas primarias, los números naturales pueden ser llamados números contables para excluir a los enteros negativos y al cero.
Los números naturales son las bases con la que muchos otros conjuntos de números pueden ser construidos por extensión: los números enteros, los números racionales, los números reales y los números complejos, entre otros.
Las propiedades de los números naturales, como la divisibilidad y la distribución de los números primarios, son estudiados en la teoría de números. Los problemas relacionados con contar y ordenar, como las enumeraciones y la partición, son estudiados en la combinatoria.
Tienen varias propiedades, como por ejemplo: la suma, la multiplicación, la resta, la división, etc.
Números ordinales y cardinales

Los números naturales pueden ser ordinales o cardinales.
Los números cardinales serían aquellos que se utilizan como números naturales, tal y como mencionamos anteriormente en los ejemplos. “Tengo dos galletas”, “Soy padre de tres hijos”, “La caja incluye dos cremas de regalo”.
Los ordinales son aquellos que expresan orden o indican una posición. Por ejemplo, en una carrera el orden de llegada de los corredores se enumera empezando por el ganador y acabando con el último que llegó a meta.
De esta manera, se dirá que el ganador es el “primero”, el siguiente el “segundo”, el siguiente el “tercero” y así hasta el último. Estos números pueden ir representados por una letra en su parte superior derecha para simplificar la escritura (1º, 2ª, 3ª, 4º, etc.).
– Números enteros

Los números enteros se componen de aquellos números naturales y sus opuestos, es decir, los números negativos (0, 1, -1, 2, -2, 50,-50…). Al igual que los números naturales, estos tampoco incluyen aquellos que tienen parte decimal.
Ejemplo de números enteros serían “Hace 30º de media en Alemania”, “Me quedé a 0 al llegar a final de mes”, “Para bajar al sótano debes marcar el botón -1 del ascensor”.
A su vez, los números enteros no pueden ser escritos con un componente fraccional. Por ejemplo, números como 8.58 o √2 no son números enteros.
Los números enteros se representan con la letra (Z). Z es un sub conjunto del grupo de números racionales Q, que a su vez forman el grupo de los números reales R. Como los números naturales, Z es un grupo contable infinito.
Los números enteros forman el grupo más pequeño y el conjunto más pequeño de los números naturales. En la teoría de números algebraicos, los números enteros son llamados a veces enteros irracionales para distinguirlos de los enteros algebraicos.
– Números racionales

El conjunto de números racionales es representado por la letra (Q) e incluyen a todos aquellos números que pueden ser escritos como una fracción de números enteros.
Es decir, este conjunto incluye números naturales (4/1), números enteros (-4/1) y números decimales exactos (15,50 = 1550/100).

La expansión decimal de un número racional siempre termina después de un número finito de dígitos (ej: 15,50) o cuando se comienza a repetir la misma secuencia finita de dígitos una y otra vez (ej: 0,3456666666666666…). Por ello, dentro del conjunto de números racionales se incluyen los números. periódicos puros o periódicos mixtos.
Adicionalmente, cualquier decimal repetido o terminal representa un número racional. Estas declaraciones son verdaderas no solo para la base 10, sino también para cualquier otra base de número entero.
Un número real que no es racional es llamado irracional. Los números irracionales incluyen a la √2, a π y e, por ejemplo. Ya que todo el conjunto de números racionales es numerable, y que el grupo de números reales no es numerable, se puede decir que casi todos los números reales son irracionales.
Los números racionales pueden ser formalmente definidos como clases de equivalencias de pares de enteros (p,q) de manera que q ≠ 0 o la relación equivalente definida por (p1,q1) (p2,q2) solo si p1,q2 = p2q1.
Los números racionales, junto con la suma y la multiplicación, forman campos que componen los números enteros y son contenidos por cualquier rama que contenga enteros.
– Números irracionales

Los números irracionales son todos los números reales que no son números racionales; los números irracionales no pueden ser expresados como fracciones. Los números racionales son los números compuestos de fracciones de números enteros.
Como consecuencia de la prueba de Cantor que dice que todos los números reales son no numerables y que los racionales si son numerables, se puede concluir que casi todos los números reales son irracionales.
Cuando el radio de longitud de dos segmentos de línea es un número irracional, se puede decir que estos segmentos de línea son inconmensurables; significando que no hay una longitud suficiente de manera que cada una de ellas pudiera ser “medida” con un entero particular múltiple del mismo.
Entre los números irracionales están el radio π de una circunferencia de círculo a su diámetro, el número de Euler (e), el número áureo (φ) y la raíz cuadrada de dos; aún más, todas las raíces cuadradas de los números naturales son irracionales. La única excepción a esta regla son los cuadrados perfectos.
Se puede observar que cuando los números irracionales son expresados de manera posicional en un sistema numeral, (como por ejemplo en los números decimales) no terminan o se repiten.
Esto quiere decir que no contienen una secuencia de dígitos, la repetición por la cual se hace una línea de la representación.

Por ejemplo: la representación decimal del número π comienza con 3.14159265358979, pero no hay un número finito de dígitos que puedan representar a π de manera exacta, ni que se puedan repetir.
La prueba de que la expansión decimal de un número racional debe terminar o repetirse es diferente a la prueba de que una extensión decimal debe ser un número racional; aunque básicas y algo largas, estas pruebas toman algo de trabajo.
Usualmente los matemáticos no toman generalmente la noción de “terminando o repitiendo” para definir el concepto de un número racional.
Los números irracionales también pueden ser tratados vía fracciones no continuas.
Referencias
- Classifyng real numbers. Recuperado de chilimath.com.
- Natural number. Recuperado de wikipedia.org.
- Clasificación de los números. Recuperado de ditutor.com.
- Recuperado de wikipedia.org.
- Irrational number. Recuperado de wikipedia.org.
