Teorema de Euclides: qué es, demostración, aplicación, ejercicios

¿Qué es el teorema de Euclides?

El teorema de Euclides demuestra las propiedades de un triángulo rectángulo al trazar una línea que lo divide en dos nuevos triángulos rectángulos que son semejantes entre sí y, a su vez, son semejantes al triángulo original; entonces, existe una relación de proporcionalidad.

Euclides fue uno de los más grandes matemáticos y geómetras de la edad antigua que realizó varias demostraciones de teoremas importantes. Uno de los principales es el que lleva su nombre, que ha tenido una amplia aplicación.

Esto ha sido así porque, a través de ese teorema, explica de forma sencilla las relaciones geométricas existentes en el triángulo rectángulo, donde los catetos de este están relacionados con sus proyecciones en la hipotenusa.

Fórmulas y demostración

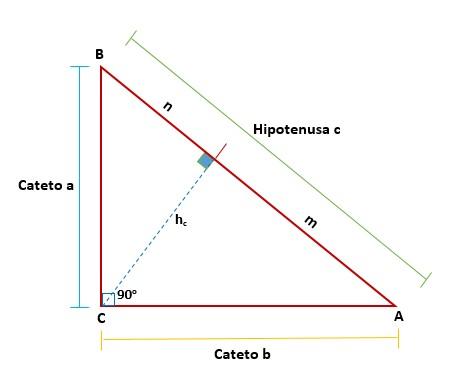
El teorema de Euclides propone que en todo triángulo rectángulo, cuando se traza una recta —que representa a la altura que corresponde al vértice del ángulo recto con respecto a la hipotenusa— se forman dos triángulos rectángulos a partir del original.

Estos triángulos serán semejantes entre sí y también serán semejantes con el triángulo original, lo que significa que sus lados semejantes son proporcionales entre sí:

Los ángulos de los tres triángulos son congruentes; es decir, que al ser rotados a 180 grados sobre su vértice, coincide un ángulo sobre el otro. Esto implica que todos serán iguales.

De esa forma también se puede verificar la semejanza que existe entre los tres triángulos, por la igualdad de sus ángulos. Desde la semejanza de triángulos, Euclides establece las proporciones de estos a partir de dos teoremas:

• Teorema de la altura.
• Teorema de los catetos.

Este teorema tiene una amplia aplicación. En la Antigüedad fue usado para calcular alturas o distancias, representando un gran avance para la trigonometría.

Actualmente es aplicado en diversas áreas que se basan en la matemática, como ingeniería, física, química y astronomía, entre muchas otras áreas.

Teorema de la altura

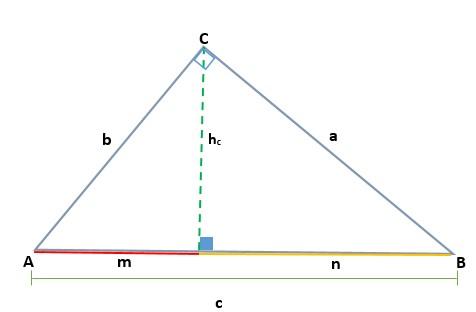
En este teorema se establece que en cualquier triángulo rectángulo, la altura trazada desde el ángulo recto con respecto a la hipotenusa es la media proporcional geométrica (el cuadrado de la altura) entre las proyecciones de los catetos que determina sobre la hipotenusa.

Es decir, el cuadrado de la altura será igual a la multiplicación de los catetos proyectados que forman la hipotenusa:

h_c² = m _* n

Demostración

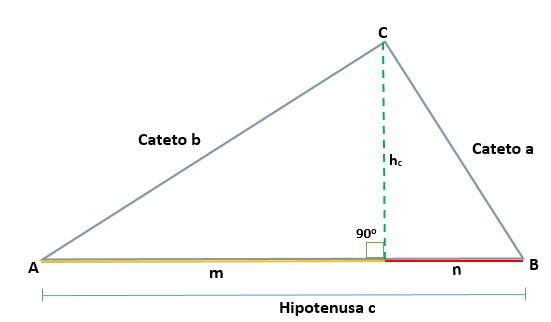
Dado un triángulo ABC, que es rectángulo en el vértice C, al trazar la altura se generan dos triángulos rectángulos semejantes, ADC y BCD; por lo tanto, sus lados correspondientes son proporcionales:

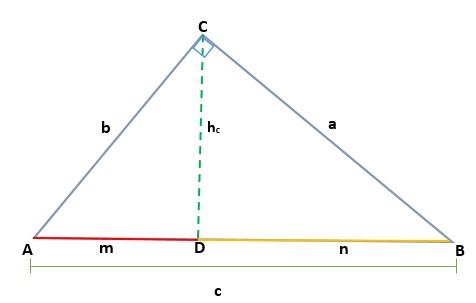
De tal forma que la altura h_c que corresponde al segmento CD, corresponde a la hipotenusa AB = c, así se tiene que:

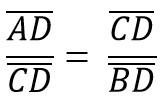
A su vez, esto corresponde a:

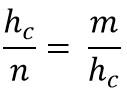
Despejando la hipotenusa (h_c), para multiplicar los dos miembros de la igualdad, se tiene que:

h_{c *} h_{c =} m _* n

h_c² = m _* n

Así, el valor de la hipotenusa es dado por:

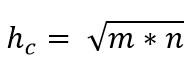
Teorema de los catetos

En este teorema se establece que, en todo triángulo rectángulo, la medida de cada cateto será la media proporcional geométrica (el cuadrado de cada cateto) entre la medida de la hipotenusa (completa) y la proyección de cada uno sobre este:

b² = c _* m

a² = c_* n

Demostración

Dado un triángulo ABC, que es rectángulo en el vértice C, de tal forma que su hipotenusa es c, al trazar la altura (h) se determinan las proyecciones de los catetos a y b, que son los segmentos m y n respectivamente, y que se encuentran sobre la hipotenusa.

Así, se tiene que la altura trazada sobre el triángulo rectángulo ABC genera dos triángulos rectángulos semejantes, ADC y BCD, de forma que los lados correspondientes son proporcionales, así:

DB = n, que es la proyección del cateto CB sobre la hipotenusa.

AD = m, que es la proyección del cateto AC sobre la hipotenusa.

Entonces, la hipotenusa c es determinada por la suma de los catetos de sus proyecciones:

c = m + n

Por la semejanza de los triángulos ADC y BCD, se tiene que:

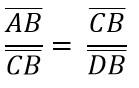
Lo anterior es lo mismo que:

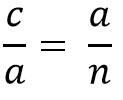
Despejando el cateto “a” para multiplicar los dos miembros de la igualdad, se tiene que:

a _* a = c _* n

a² = c _* n

Así, el valor del cateto “a” es dado por:

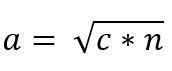
De igual forma, por la semejanza de los triángulos ACB y ADC, se tiene que:

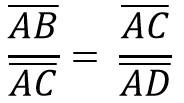
Lo anterior es igual a:

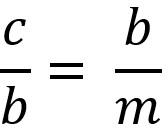
Despejando el cateto “b” para multiplicar los dos miembros de la igualdad, se tiene que:

b _* b = c _* m

b² = c _* m

Así, el valor del cateto “b” es dado por:

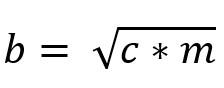
Relación entre los teoremas de Euclides

Los teoremas con referencia a la altura y los catetos se relacionan entre sí porque la medida de ambos se hace respecto a la hipotenusa del triángulo rectángulo.

A través de la relación de los teoremas de Euclides el valor de la altura también puede ser hallado; eso es posible despejando los valores de m y n del teorema de los catetos y se reemplazan en el teorema de la altura. De esa forma se cumple que la altura es igual a la multiplicación de los catetos, divididos entre la hipotenusa:

b² = c _* m

m = b² ÷ c 

a² = c _* n

n =a² ÷ c

En el teorema de la altura se reemplaza m y n:

h_c² = m _* n

h_c² = (b² ÷ c) _* (a² ÷ c)

h_c = (b²_* a²) ÷ c

Ejercicios resueltos

Ejemplo 1

Dado el triángulo ABC, rectángulo en A, determinar la medida de AC y AD,  si AB = 30 cm y BD = 18 cm

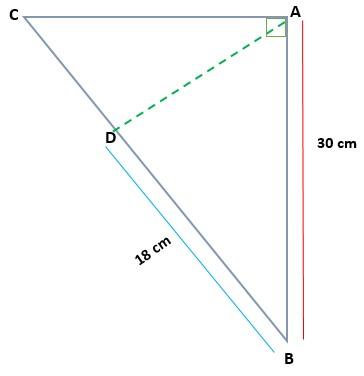
Solución

En este caso se tienen las medidas de uno de los catetos proyectados (BD) y de uno de los catetos del triángulo original (AB). De esa forma se puede aplicar el teorema de los catetos para hallar el valor del cateto BC.

AB² = BD _* BC

(30)² = 18 _* BC

900 = 18 _* BC

BC = 900 ÷ 18

BC = 50 cm

El valor del cateto CD puede ser hallado sabiendo que BC = 50:

CD = BC – BD

CD = 50 – 18 = 32 cm

Ahora sí es posible determinar el valor del cateto AC, aplicando nuevamente el teorema de los catetos:

AC² = CD _* BD

AC² = 32 _* 50

AC² = 160

AC = √1600 = 40 cm

Para determinar el valor de la altura (AD) se aplica el teorema de la altura, ya que los valores de los catetos proyectados CD y BD son conocidos:

AD² = 32 _* 18

AD² = 576

AD = √576

AD = 24 cm

Ejemplo 2

Determinar el valor de la altura (h) de un triángulo MNL, rectángulo en N, sabiendo las medidas de los segmentos:

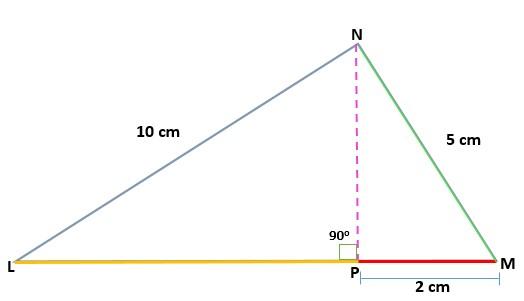
NL = 10 cm

MN = 5 cm

PM = 2 cm

Solución

Se tiene la medida de uno de los catetos proyectados sobre la hipotenusa (PM), así como también las medidas de los catetos del triángulo original. De esa forma se puede aplicar el teorema de los catetos para hallar el valor del otro cateto proyectado (LN):

NL² = PM _* LM

(10)² = 5 _* LM

100 = 5 _* LM

PL = 100 ÷ 5 = 20

Como ya se conoce el valor de los catetos y la hipotenusa, a través de la relación de los teoremas de la altura y los catetos se puede determinar el valor de la altura:

NL = 10

MN = 5

LM = 20

h = (b²_* a²) ÷ c.

h =  (10²_* 5²)  ÷ (20)

h = (100 _* 25) ÷ (20)

h = 2500 ÷ 20

h = 125 cm.