Componentes Rectangulares de un Vector (con Ejercicios)
Las componentes rectangulares de un vector son los datos que conforman dicho vector. Para determinarlos, es necesario tener un sistema de coordenadas, el cual generalmente es el plano cartesiano.
Una vez que se tiene un vector en un sistema de coordenadas, se pueden calcular sus componentes. Estas son 2, un componente horizontal (paralela al eje X), llamada “componente en el eje X”, y un componente vertical (paralela al eje Y), llamada “componente en el eje Y”.

Para poder determinar los componentes es necesario conocer ciertos datos del vector como son su magnitud y el ángulo que este forma con el eje X.
Índice del artículo
Para determinar estos componentes, se deben conocer ciertas relaciones entre los triángulos rectángulos y las funciones trigonométricas.
En la siguiente imagen se puede apreciar dicha relación.
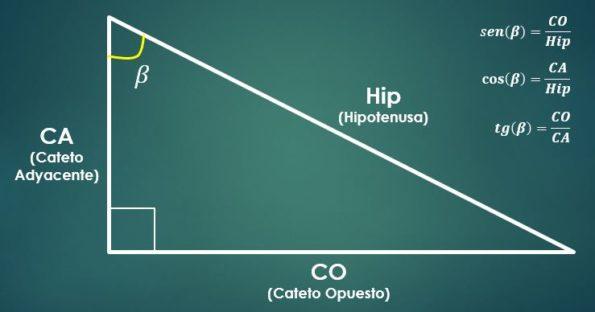
El seno de un ángulo es igual al cociente entre la medida del cateto opuesto al ángulo y la medida de la hipotenusa.
Por otro lado, el coseno de un ángulo es igual al cociente entre la medida del cateto adyacente al ángulo y la medida de la hipotenusa.
La tangente de un ángulo es igual al cociente entre la medida del cateto opuesto y la medida del cateto adyacente.
En todas estas relaciones es necesario establecer el triángulo rectángulo correspondiente.
Sï. Dependiendo de los datos que sean proporcionados, la forma de calcular las componentes rectangulares de un vector puede variar. Otra herramienta que se utiliza mucho es el Teorema de Pitágoras.
En los siguientes ejercicios se pone en práctica la definición de las componentes rectangulares de un vector y las relaciones descritas arriba.
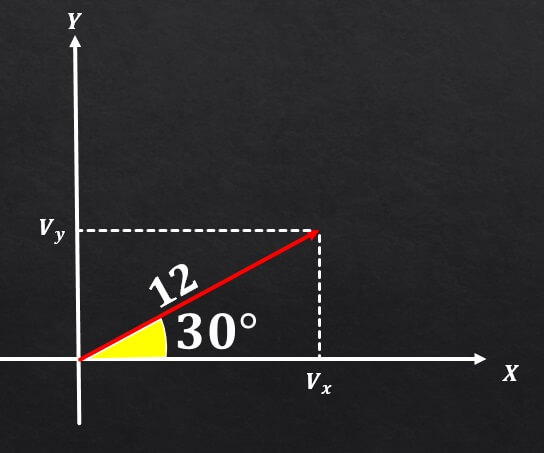
Se sabe que un vector A tiene magnitud igual a 12 y el ángulo que este forma con el eje X tiene una medida de 30°. Determine las componentes rectangulares de dicho vector A.
Solución
Si se aprecia la imagen y se utilizan las formulas descritas anteriormente se puede concluir que la componente en el eje Y del vector A es igual a
sen(30°)=Vy / 12 , y por tanto Vy = 12*(1/2)= 6.
Por otro lado, se tiene que la componente en el eje X del vector A es igual a
cos(30°)=Vx / 12 , y por tanto Vx = 12*(√3 /2)= 6√3.
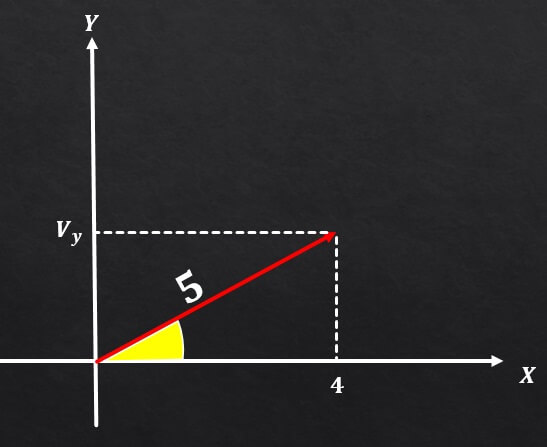
Si el vector A tiene una magnitud igual a 5 y la componente en el eje X es igual a 4, determine el valor de la componente de A en el eje y.
Solución
Utilizando el Teorema de Pitágoras, se tiene que la magnitud del vector A elevada al cuadrado es igual a la suma de los cuadrados de las dos componentes rectangulares. Es decir, M²= (Vx)² + (Vy)².
Sustituyendo los valores proporcionados, se tiene que
5²= (4)² + (Vy)², por lo tanto, 25=16+(Vy)².
Esto implica que (Vy)²=9 y en consecuencia Vy=3.
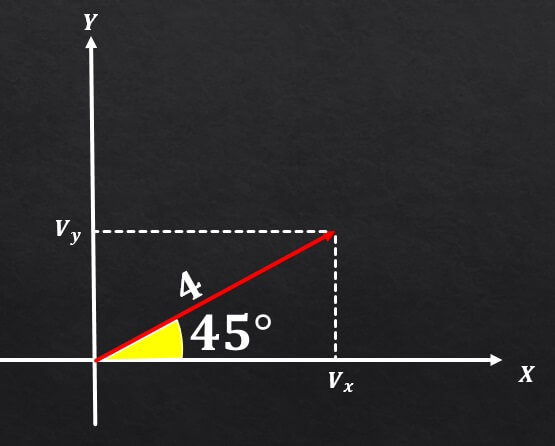
Si el vector A tiene una magnitud igual a 4 y este forma un ángulo de 45° con el eje X, determine las componentes rectangulares de dicho vector.
Solución
Utilizando las relaciones entre un triángulo rectángulo y las funciones trigonométricas, se puede concluir que la componente en el eje Y del vector A es igual a
sen(45°)=Vy / 4 , y por tanto Vy = 4*(√2 /2)= 2√2.
Por otro lado, se tiene que la componente en el eje X del vector A es igual a
cos(45°)=Vx / 4 , y por tanto Vx = 4*(√2 /2)= 2√2.
- Landaverde, F. D. (1997). Geometría (Reprint ed.). Progreso.
- Leake, D. (2006). Triángulos (illustrated ed.). Heinemann-Raintree.
- Pérez, C. D. (2006). Precálculo. Pearson Educación.
- Ruiz, Á., & Barrantes, H. (2006). Geometrías. Tecnológica de CR.
- Sullivan, M. (1997). Precálculo. Pearson Educación.
- Sullivan, M. (1997). Trigonometría y Geometría Analítica. Pearson Educación.
