Programación lineal: para qué sirve, modelos, restricciones, aplicaciones

La programación lineal es un método matemático que sirve para optimizar (maximizar o minimizar según se requiera) una función cuyas variables están sujetas a restricciones, siempre y cuando la función y las restricciones sean linealmente dependientes de las variables.

Generalmente la función a optimizar modela una situación práctica, como por ejemplo la ganancia de un fabricante cuyos insumos, mano de obra o maquinaria son limitados.

Uno de los casos más sencillos es el de una función lineal a maximizar, que solo depende de dos variables, llamadas variables de decisión. Puede ser de la forma:

Z = k₁x + k₂y

Con k₁ y k₂ constantes. A esta función se le conoce como la función objetivo. Desde luego existen situaciones que ameritan más de dos variables para su estudio, siendo más complejas:

Z = k₁x₁ + k₂x₂ + k₃x₃ +….

Y las restricciones también se modelan matemáticamente mediante un sistema de ecuaciones o inecuaciones, igualmente lineales en x e y.

El conjunto de soluciones de este sistema se llama soluciones factibles o puntos factibles. Y entre los puntos factibles existe al menos uno, que optimiza la función objetivo.

La programación lineal fue desarrollada de manera independiente por el físico y matemático estadounidense George Dantzig (1914-2005) y el matemático y economista ruso Leonid Kantorovich (1912-1986) poco después de la Segunda Guerra Mundial.

El método de solución de problemas conocido como método simplex es creación de Dantzig, quien trabajó para la fuerza aérea norteamericana, la Universidad de Berkeley y la Universidad de Stanford.

Índice del artículo

• 1 Modelos de programación lineal
• 2 Ejemplo de modelo
• 3 Métodos de solución
  • 3.1 – Método gráfico o geométrico
  • 3.2 – Método simplex de Dantzig
• 4 Aplicaciones
• 5 Ejercicios resueltos
  • 5.1 – Ejercicio 1
  • 5.2 – Ejercicio 2
• 6 Referencias

Modelos de programación lineal

Los elementos necesarios para establecer un modelo de programación lineal, adecuado a una situación práctica, son:

-Función objetivo

-Variables de decisión

-Restricciones

En la función objetivo se define lo que se quiere lograr. Por ejemplo, supongamos que se desea maximizar las ganancias obtenidas de la fabricación de determinados productos. Entonces se establece la función “ganancia”, según el precio al que se venden los productos.

En términos matemáticos, dicha función puede expresarse abreviadamente usando la notación de sumatoria:

Z = ∑k_i x_i

En esta ecuación, k_i son coeficientes y x_i son las variables de decisión.

Las variables de decisión son los elementos del sistema cuyo control se tiene y sus valores son números reales positivos. En el ejemplo propuesto, las variables de decisión son la cantidad de cada producto a fabricar para obtener la ganancia máxima.

Por último, tenemos las restricciones, que son ecuaciones o inecuaciones lineales en términos de las variables de decisión. En ellas se describen las limitaciones al problema, que son conocidas y pueden ser por ejemplo las cantidades de materia prima disponible en la fabricación.

Tipos de restricciones

Se puede tener una cantidad M de limitaciones, comenzando desde j = 1 hasta j = M. Matemáticamente las restricciones son de tres tipos:

1. A_j = ∑ a_ij . x_i
2. B_j ≥ ∑ b_ij . x_i
3. C_j ≤ ∑ c_ij . x_i

La primera restricción es de tipo ecuación lineal y significa que el valor A_j, el cual es conocido, tiene que ser respetado.

Las dos restricciones restantes son inecuaciones lineales y significa que los valores B_j y C_j, conocidos, pueden respetarse o superarse, cuando el símbolo que aparece es ≥ (mayor o igual que) o bien respetarse o no superarse, si el símbolo es ≤ (menor o igual que).

Ejemplo de modelo

Los campos de aplicación son muy diversos, abarcando desde administración de empresas hasta nutrición, pero para entender el método, se propone seguidamente un modelo sencillo de una situación práctica con dos variables.

Una pastelería local es conocida por dos especialidades: la torta selva negra y la torta sacripantina.

En su elaboración requieren huevos y azúcar. Para la selva negra se necesitan 9 huevos y 500 g de azúcar, mientras que para la sacripantina son necesarios 8 huevos y 800 g de azúcar. Los respectivos precios de venta son 8 y 10 $.

El problema es: ¿Cuántas tortas de cada tipo debe fabricar la pastelería para maximizar su ganancia, sabiendo que dispone de 10 kilos de azúcar y 144 huevos?

Variables de decisión

Las variables de decisión son “x” e “y”, las cuales toman valores reales:

-x: la cantidad de tortas tipo selva negra

-y: las tortas tipo sacripantina.

Restricciones

Las restricciones vienen dadas por el hecho de que el número de tortas es una cantidad positiva y hay cantidades limitadas de materia prima para prepararlas.

Por lo tanto, en forma matemática, dichas restricciones adquieren la forma:

1. x ≥ 0
2. y ≥0
3. 9x +8y ≤ 144
4. 0.5 x + 0.8y ≤ 10

Las restricciones 1 y 2 constituyen la condición de no negatividad expuesta anteriormente, y todas las inecuaciones planteadas son lineales. En las  restricciones 3 y 4 están los valores que no deben superarse: 144 huevos y 10 kg de azúcar.

Función objetivo

Finalmente, la función objetivo es la ganancia obtenida al fabricar “x” cantidad de tortas selva negra más “y” cantidad de sacripantinas. Se construye multiplicando precio por cantidad de tortas confeccionadas y sumando para cada tipo. Se trata de una función lineal a la que llamaremos G(x,y):

G = 8x + 10y

Métodos de solución

Entre las diversas metodologías de solución se encuentran los métodos gráficos, el algoritmo simplex y el método del punto interior, por mencionar algunos.

– Método gráfico o geométrico

Cuando se tiene un problema de dos variables como el de la sección anterior, las restricciones determinan una región poligonal en el plano xy, llamada región factible o región de viabilidad.

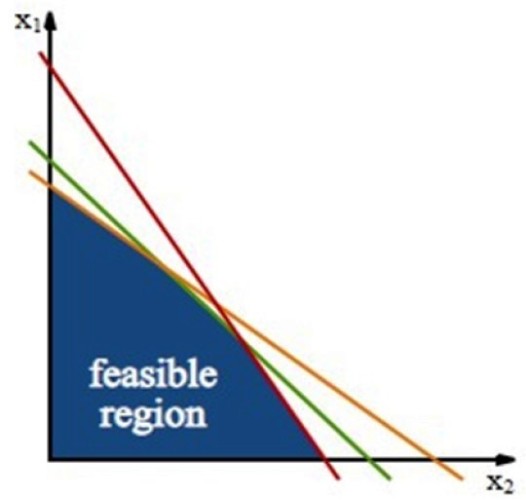
Dicha región se construye mediante las rectas de restricción, que son las rectas obtenidas a partir de las inecuaciones de las restricciones, trabajando únicamente con el signo de igualdad.

En el caso de la pastelería que desea optimizar las ganancias, las rectas de restricción son:

1. x=0
2. y=0
3. 9x +8y = 144
4. 0.5 x + 0.8y = 10

Todos los puntos de la región encerrada por estas rectas son posibles soluciones, así que hay infinitas de ellas. Excepto en el caso en que la región factible resulte vacía, en cuyo caso el problema planteado carece de solución.

Afortunadamente, para el problema de la pastelería la región factible no es vacía, la tenemos a continuación.

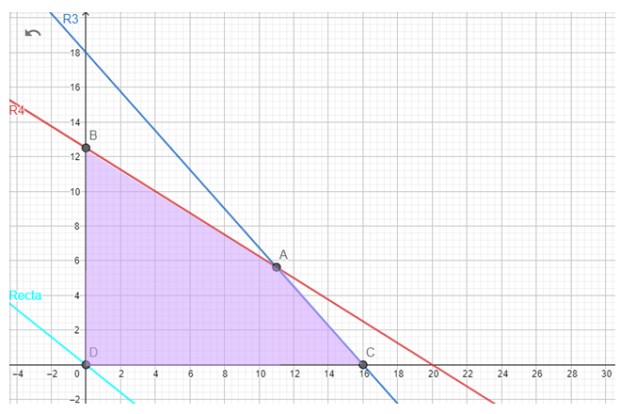
La solución óptima, si es que existe, se encuentra con la ayuda de la función objetivo. Por ejemplo, cuando se trata de encontrar la ganancia máxima G, se tiene la siguiente recta, a la cual se denomina recta de iso-beneficio:

G = k₁x + k₂y → y = -k₁x / k₂ + G/ k₂

Con esta recta se obtienen todos los pares (x,y) que proporcionan una ganancia dada G, así que hay una familia de rectas según el valor de G, pero todas con la misma pendiente -k₁ / k₂, de manera que son rectas paralelas.

La solución óptima

Ahora bien, se puede demostrar que la solución óptima de un problema lineal siempre es un punto extremo o vértice de la región factible. Entonces:

La recta solución es la más alejada del origen y que tenga al menos un punto en común con la región factible.

Si la recta más cercana al origen tiene todo un segmento en común con la región factible, se dice que hay infinitas soluciones. Este caso ocurre si la pendiente de la recta de iso-beneficios es igual a la de alguna de las otras rectas que limitan la región.

Para nuestra pastelería, los vértices candidatos son  A, B y C.

– Método simplex de Dantzig

El método gráfico o geométrico es aplicable para dos variables. Sin embargo, resulta más complicado cuando hay tres variables, e imposible de utilizar para un número mayor de variables.

Cuando se trata de problemas de más de dos variables se emplea el método simplex, que consiste en una serie de algoritmos para optimizar las funciones objetivos. Suelen utilizarse matrices y aritmética sencilla para llevar a cabo los cálculos.

El método simplex comienza eligiendo una solución factible y comprobando si es óptima. Si lo es ya tenemos resuelto el problema, pero si no lo es, se continúa hacia una solución más cercana a la optimización. Si la solución existe, el algoritmo da con ella en unos cuantos intentos.

Aplicaciones

La programación lineal y la no-lineal se aplican en muchos campos para tomar las mejores decisiones en cuanto a disminuir costos y aumentar las ganancias, que no siempre son monetarias, ya que pueden medirse en tiempo por ejemplo, si se busca minimizar el tiempo necesario para llevar a cabo una serie de operaciones.

He aquí algunos campos:

-En marketing se emplea para hallar la mejor combinación de medios (redes sociales, televisión, prensa y otros) para publicitar cierto producto.

-Para la asignación de labores adecuadas al personal de una empresa o fábrica o de horarios a los mismos.

-En la selección del alimento más nutritivo y al menor costo en las industrias ganaderas y avícolas.

Ejercicios resueltos

– Ejercicio 1

Resolver gráficamente el modelo de programación lineal planteado en las secciones precedentes.

Solución

Es preciso graficar el conjunto de valores determinados por el sistema de restricciones especificado en el problema:

1. x ≥ 0
2. y ≥0
3. 9x +8y ≤ 144
4. 0.5 x + 0.8y ≤ 10

La región dada por las inecuaciones 1 y 2 corresponde al primer cuadrante del plano cartesiano. En cuanto a las inecuaciones 3 y 4, se comienza por encontrar las rectas de restricción:

9x +8y = 144

0.5 x + 0.8y = 10 → 5x + 8y =100

La región factible es un cuadrilátero cuyos vértices son los puntos A, B, C y D.

La ganancia mínima es 0, por lo tanto la recta 8x + 10y = 0 es el límite inferior y las rectas de iso-beneficio tienen pendiente -8/10 = – 0.8.

Este valor es diferente de las pendientes de las otras rectas de restricción y como la región factible es acotada, existe la solución única.

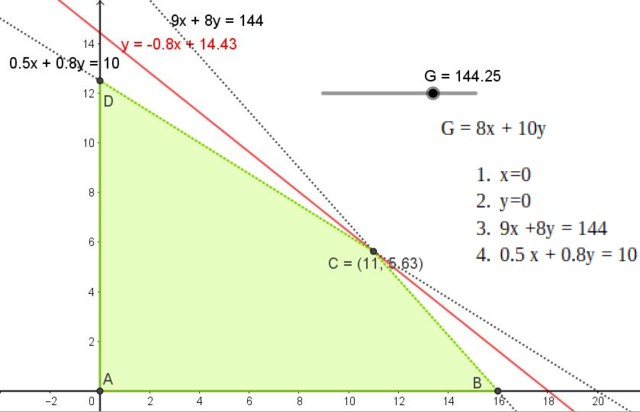
Dicha solución corresponde a una recta de pendiente -0.8 que pasa por alguno de los puntos A, B o C, cuyas coordenadas son:

A ( 11; 5.625)

B (0; 12.5)

C (16, 0)

Solución óptima

Calculamos el valor de G para cada uno de estos puntos:

-(11; 5.625): G_A = 8 x 11 + 10 x 5.625 = 144.25

-(0; 12.5): G_B = 8 x 0 + 10 x 12.5 = 125

-(16, 0): G_C = 8 x 16 + 10 x 0 = 128

La mayor ganancia se encuentra fabricando 11 tortas de selva negra y 5.625 tortas sacripantinas. Esta solución concuerda con la encontrada a través del software.

– Ejercicio 2

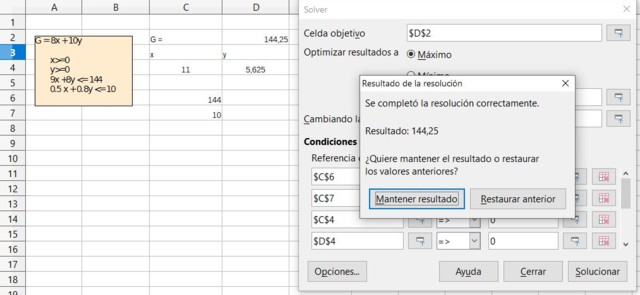
Verificar el resultado  del ejercicio anterior mediante el uso de la función Solver (Solucionador) disponible en la mayoría de las hojas de cálculo como Excel o Calc de LibreOffice, los cuales incorporan el algoritmo Simplex para la optimización en programación lineal.

Solución

Referencias

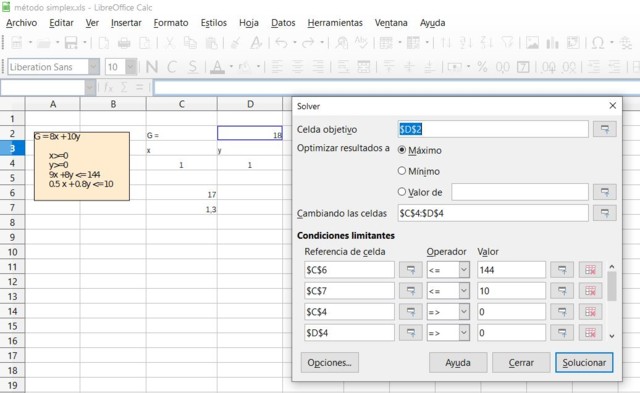
1. Brilliant. Linear Programming. Recuperado de: brilliant.org.
2. Eppen, G. 2000. Investigación de Operaciones en la Ciencia Administrativa. 5ta. Edición. Prentice Hall.
3. Haeussler, E. 1992. Matemáticas para Administración y Economía. 2da. Edición. Grupo Editorial Iberoamericana.
4. Hiru.eus. Programación lineal. Recuperado de: hiru.eus.
5. Wikipedia. Programación lineal. Recuperado de: es. wikipedia.org.