Función decreciente: cómo identificarla, ejemplos, ejercicios

Una función decreciente f es aquella cuyo valor disminuye a medida que aumenta el valor de x. Significa que en un intervalo dado, considerando dos valores x₁ y x₂ tales que x₁ x₂, entonces f (x₁) > f (x₂).

Un ejemplo de una función que siempre es decreciente es f(x) = -x³, cuya gráfica se muestra en la siguiente figura:

Aunque algunas funciones como esta se caracterizan por ser decrecientes en todo su dominio, no todas se comportan así, las hay que son crecientes y también aquellas que crecen y decrecen en determinados intervalos del dominio. Al estudio de los intervalos de crecimiento y decrecimiento se le llama monotonía de la función.

Asimismo se puede considerar el crecimiento o decrecimiento de la función en un determinado punto del dominio. Pero toda función que sea decreciente en un intervalo dado, lo es también en todo punto que pertenece a él.

Índice del artículo

• 1 ¿Cómo identificar una función decreciente?
  • 1.1 Criterio de la primera derivada
• 2 Teorema para funciones decrecientes y crecientes
  • 2.1 Demostración
• 3 Pasos para saber si una función es decreciente
• 4 Ejemplos de funciones decrecientes
  • 4.1 La función exponencial
  • 4.2 La función 1/x
  • 4.3 La función afín
• 5 Ejercicio resuelto
  • 5.1 Solución
• 6 Referencias

¿Cómo identificar una función decreciente?

La gráfica de la función indica visualmente si es decreciente o no. Si al desplazarse en sentido creciente de las x,  la función “desciende”, significa que es decreciente.

Y si tiene intervalos en los que decrece y crece alternativamente, que es lo más usual, pues estos se ponen de manifiesto claramente observando el comportamiento de la función a lo largo de su dominio, ya que habrá intervalos en que la función “ascienda” y otros en que “descienda”.

Alternativamente, si no se dispone de la gráfica de la función, analíticamente es posible determinar si es decreciente en un punto o en un intervalo, a través de la primera derivada.

Criterio de la primera derivada

Obsérvese el comportamiento de la función decreciente mostrada en la figura 2. Los segmentos de recta en color rosa son tangentes a los puntos cuyas coordenadas son [a, f(a)] y [a+h, f(a+h)] y tienen pendiente negativa.

Para esta función se cumple lo siguiente:

f (a+h) – f (a) 0 ⇒  f (a+h) f (a)

Por lo tanto se puede pensar que la función es decreciente en x = a.

Ahora bien, la primera derivada de la función f(x), evaluada en x = a, que por definición es la pendiente de la recta tangente a la curva en x = a, viene dada por:

El límite indica que el valor de h se puede hacer tan pequeño como se quiera y sugiere que el signo de f´(a), puede utilizarse para saber si la función es o no decreciente en un punto en particular, siempre y cuando la derivada exista en ese punto.

Entonces, si f´(a) 0, se puede afirmar que la función es decreciente, y por el contrario, si f´(a) > 0, entonces la función es creciente en dicho punto.

Teorema para funciones decrecientes y crecientes

Anteriormente se hizo referencia al comportamiento de la función en un punto. Ahora, el siguiente teorema permite conocer los intervalos en que una función es decreciente, creciente o constante:

Sea f una función diferenciable en el intervalo (a,b). Se cumple que:

-Si f´(x) 0 para todo x perteneciente a (a,b), entonces f(x) es decreciente en (a,b).

-Si por el contrario f´(x) > 0 para todo x perteneciente a (a,b), se dice que la función f(x) es creciente en (a,b).

-Finalmente, si f´(x) = 0 para todo x que pertenece al intervalo (a,b), f(x) es constante en dicho intervalo.

Demostración

Supóngase que f´(x) 0 para cualquier valor de x en el intervalo (a,b), además se tienen x₁ y x₂ pertenecientes a dicho intervalo y la condición de que x₁ x₂.

El teorema del valor medio afirma que existe un número real c, comprendido entre x₁ y x₂, tal que:

Como está establecido ya que x₁ x₂,  Δx es positivo. Entonces, como f´(c) es negativo, entonces Δy lo es también. Por lo tanto f(x₁) es mayor que f(x₂) y la función efectivamente decrece en todo punto del intervalo (a,b).

Pasos para saber si una función es decreciente

Para encontrar los intervalos de decrecimiento y crecimiento de una función mediante la aplicación del teorema anterior, se siguen estos pasos:

-Hallar la primera derivada de la función e igualarla a cero, resolviendo la ecuación resultante. Asimismo determinar los puntos en que la derivada no exista.

Todos estos puntos se denominan puntos críticos y es necesario hallarlos, puesto que en ellos la derivada tiene oportunidad de cambiar su signo, indicativo de que la función pasa de creciente a decreciente o al contrario.

-El dominio de la función se divide en intervalos determinados por los puntos en que la primera derivada se anula o no existe.

-Por último se estudia el signo de la derivada en un punto arbitrario que pertenezca a cada uno de los intervalos obtenidos en el paso anterior.

Ejemplos de funciones decrecientes

Las funciones no decrecen todas al mismo ritmo, algunas lo hacen más rápido que otras. Las siguientes funciones, que aparecen con frecuencia en la práctica, son decrecientes:

La función exponencial

Una función de la forma f(x) = a^x, con a comprendido entre 0 y 1, sin incluir a estos, decrece rápidamente a lo largo de su dominio.

La función 1/x

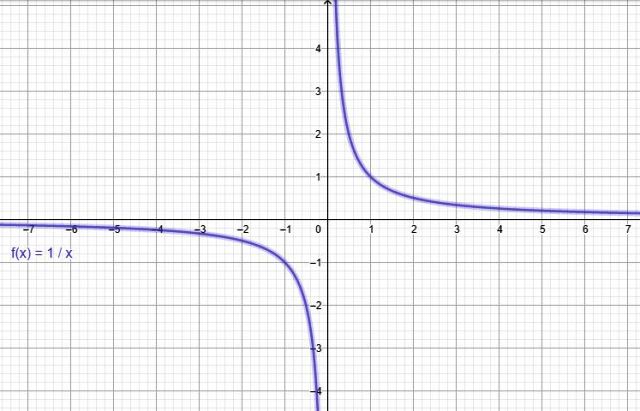
Mediante un programa graficador en línea como Geogebra se construye la gráfica de la función f(x) = 1/x, constatando que es decreciente en todo su dominio.

La función afín

La funciones de la forma y = mx + b con m0 tienen gráficas que son rectas de pendiente negativa y por lo tanto son funciones decrecientes.

Ejercicio resuelto

Hallar, si los hay, los intervalos de decrecimiento de la función:

f (x) = x⁴ – 6x² – 4

Solución

El primer paso es hallar f´(x):

f´(x) = 4x³ – 12x

La primera derivada de f(x) es una función continua, es decir, no tiene puntos de discontinuidad, pero se anula en:

4x³ – 12x = 0 = 4x(x²-3) = 0

Las soluciones de esta ecuación son: x₁ = 0, x₂ = – √3 y x₃ = √3. Estos son los puntos críticos, que dividen al dominio de f(x) en los intervalos: (-∞,- √3); (- √3,0); (0, √3); (√3, ∞+).

Seguidamente se evalúa la primera derivada en un valor de x arbitrario, que pertenezca a cada intervalo. Se eligieron estos valores:

Para (-∞,- √3)

f´(-2) = 4(-2)³ – 12x(-2) = -32+24 = -8

Para (- √3,0)

f´(-1) = 4(-1)³ – 12x(-1) = -4+12 = 8

Para (0, √3)

f´(1) = 4(1)³ – 12x(1) = 4-12 = -8

Para (√3, ∞+)

f´(2) = 4(2)³ – 12x(2) = 32-24 = 8

Como son varios intervalos, es buena idea hacer una tabla para organizar los resultados. La flecha hacia arriba indica que la función crece y hacia abajo, que decrece:

Se concluye que la función decrece en los intervalos (-∞,- √3) y (0, √3) y crece en los restantes intervalos. Se comprueba fácilmente graficando la función original en Geogebra.

Referencias

1. Ayres, F. 2000. Cálculo. 5ed. Mc Graw Hill.
2. Leithold, L. 1992. Cálculo con Geometría Analítica. HARLA, S.A.
3. Purcell, E. J., Varberg, D., & Rigdon, S. E. (2007). Cálculo. México: Pearson Educación.
4. Matemóvil. Funciones, crecientes, decrecientes y constantes. Recuperado de: matemovil.com
5. Stewart, J. 2006. Precálculo: Matemáticas para el Cálculo. 5ta. Edición. Cengage Learning.