Método del paralelogramo: ejemplos, ejercicios resueltos
El método del paralelogramo es un método gráfico para sumar dos vectores en el plano. Se utiliza con frecuencia para encontrar la resultante de dos fuerzas aplicadas a un cuerpo o de dos velocidades, como en el caso de un nadador que pretende cruzar perpendicularmente un río y es desviado por la corriente.
Para construir el paralelogramo, los orígenes de los vectores a sumar, dibujados a escala, deben coincidir en un punto.
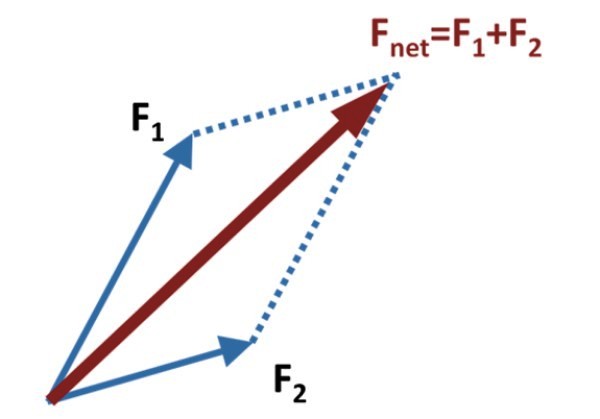
Luego se dibujan líneas auxiliares paralelas a cada vector, que lleguen hasta el extremo del otro, tal como se muestra en la figura superior.
El vector suma o resultante, también llamado fuerza neta, es el vector Fnet, que se obtiene dibujando el vector que va desde el origen común de F1 y F2, hasta el punto donde se intersectan las líneas paralelas auxiliares. En el diagrama de la figura estas se representan mediante líneas punteadas.
El método recibe su nombre de la figura que se forma con los vectores sumandos y las líneas auxiliares, que es precisamente un paralelogramo. La diagonal principal del paralelogramo es el vector suma.
Es muy importante destacar que el orden en que se coloquen los vectores sumandos no altera para nada la suma, ya que esta operación entre vectores es conmutativa.
Índice del artículo
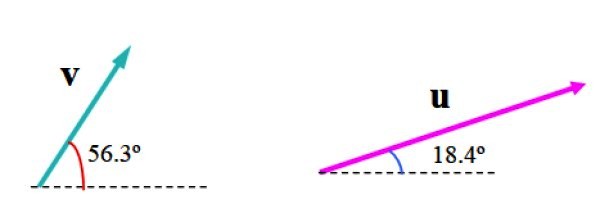
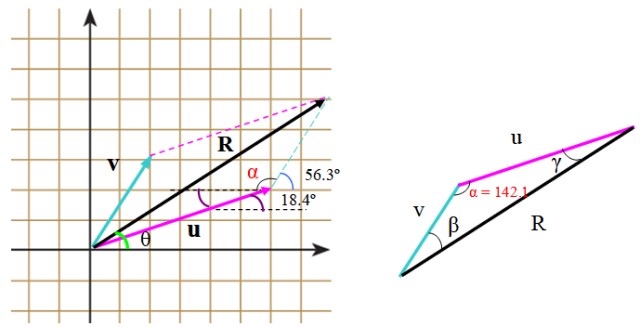
En la siguiente imagen se muestran los vectores v y u en unidades arbitrarias. El vector v mide 3.61 unidades y forma un ángulo de 56.3º con la horizontal, mientras que u mide 6.32 unidades y ángulo de 18.4º respecto a dicha línea de referencia.
Vamos a encontrar su vector suma mediante el método del paralelogramo.
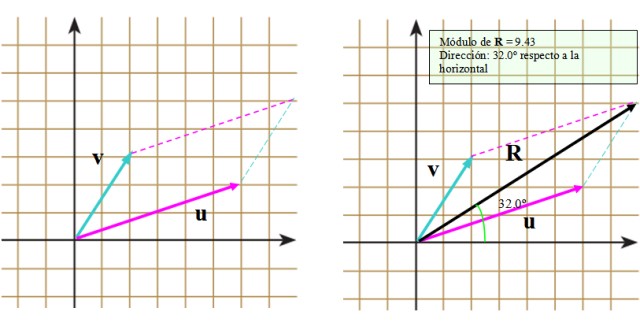
Es preciso escoger una escala apropiada, como por ejemplo la que se muestra en la siguiente figura, en la cual el plano se ha dividido mediante una cuadrícula. El ancho del cuadrado representa una (1) unidad.
Como los vectores no se alteran al ser trasladados, se colocan de tal manera que sus orígenes coincidan con el origen del sistema de coordenadas (imagen de la izquierda).
Ahora sigamos estos pasos:
- Trazar por el extremo del vector v una línea segmentada que sea paralela al vector u.
- Repetir el procedimiento pero esta vez con el extremo del vector u.
- Dibujar la diagonal principal que se extiende desde el origen común hasta el punto de intersección de las líneas segmentadas.
El resultado se aprecia en la imagen derecha, en la que aparece el vector resultante R.
Si queremos conocer la magnitud de R, podemos medir su longitud y compararla con la escala que tenemos. Y en cuanto a su dirección, pueden utilizarse como referencias el eje horizontal o el eje vertical, por ejemplo.
Al utilizar el eje horizontal o eje x, el ángulo que R forma con dicho eje se mide con el transportador y de esta forma conocemos la dirección de R.
Asimismo, la magnitud y dirección de R pueden calcularse mediante los teoremas del coseno y el seno, ya que el paralelogramo formado puede dividirse en dos triángulos congruentes, cuyos lados son los módulos de los vectores u, v y R. Véase el ejemplo resuelto 1.
Cuando los vectores son perpendiculares entre sí, la figura que se forma es un rectángulo. El módulo del vector resultante corresponde a la longitud de la diagonal, que puede calcularse fácilmente mediante el teorema de Pitágoras.
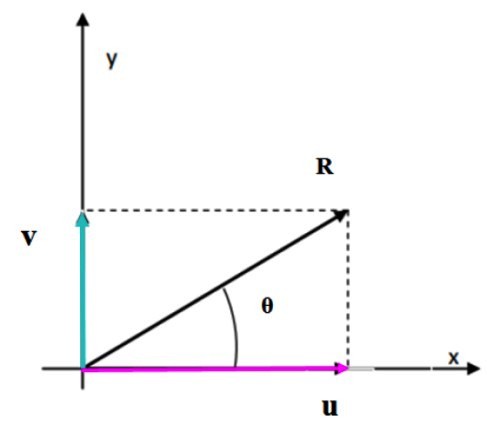
Se tiene el vector v, que mide 3.61 unidades y forma un ángulo de 56.3º con la horizontal, y el vector u, cuya medida es 6.32 unidades y forma un ángulo de 18.4º (figura 2). Determinar el módulo del vector resultante R = u + v y la dirección que forma dicho vector con el eje horizontal.
Solución
Se aplica el método del paralelogramo según los pasos descritos más arriba, para obtener el vector R. Como se dijo antes, si los vectores se dibujan cuidadosamente siguiendo la escala y usando regla y transportador, la magnitud y la dirección de R se miden directamente sobre el dibujo.
También se pueden calcular directamente, con ayuda de la trigonometría y las propiedades de los ángulos. Cuando el triángulo formado no es rectángulo, como en este caso, se aplica el teorema del coseno para encontrar el lado faltante.
En el triángulo de la derecha, los lados miden u, v y R. Para aplicar el teorema del coseno se requiere saber el ángulo que hay entre v y u, que podemos encontrar con ayuda de la cuadrícula, posicionando adecuadamente los ángulos suministrados por el enunciado.
Dicho ángulo es α y está compuesto de:
α = (90-56.3º) + 90º +18.4º = 142.1º
Según el teorema del coseno:
R2 = v2 + u2 – 2u⋅v⋅cos α = 3.612 + 6.322 – 2× 3.61 × 6.32 × cos 142.1º = 88.98
R = 9.43 unidades.
Por último, el ángulo que hay entre R y el eje horizontal es θ=18.4 º + γ. El ángulo γ se puede encontrar mediante el teorema del seno:
sen α / R = sen γ / u
Por lo tanto:
sen γ = v (sen α / R) = 3.61 x (sen 142.1º / 9.43)
γ = 13.6º
θ = 18.4 º + 13.6 º = 32º
Un nadador se dispone a cruzar un río nadando perpendicularmente a la corriente con velocidad constante de 2.0 m/s. El nadador parte de A, sin embargo termina en B, un punto aguas abajo, debido a la corriente que lo desvió.
Si la velocidad de la corriente es 0.8 m/s y todas las velocidades se suponen constantes, hallar la velocidad del nadador tal como lo ve un observador parado en la orilla.
Solución
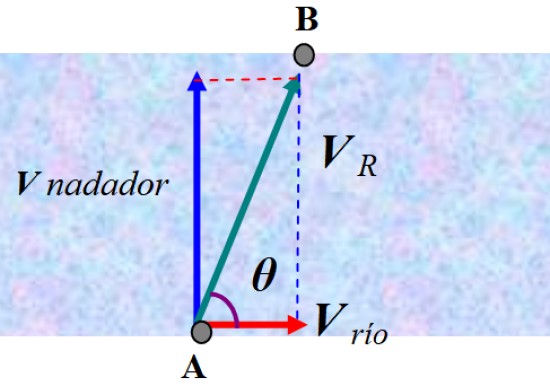
Un observador parado en la orilla vería cómo el nadador es desviado según la velocidad resultante VR. Para encontrar la respuesta necesitamos sumar vectorialmente la velocidad del nadador respecto al agua y la velocidad de la corriente, a la que llamamos V río:
V R = V nadador + V río
En la figura, que no está a escala, se sumaron los vectores para obtener V R. En este caso se puede aplicar el teorema de Pitágoras para obtener su magnitud:
VR2 = 2.02 + 0.82 = 4.64
VR = 2.15 m/s
La dirección en que se desvía el nadador de la dirección perpendicular se calcula fácilmente, notando que:
θ = arctg (2/0.8) = 68.2º
Entonces el nadador se desvía 90º – 68.2º = 27.2º de su dirección original.
- Bauer, W. 2011. Física para Ingeniería y Ciencias. Volumen 1. Mc Graw Hill.
- Bedford, 2000. A. Mecánica para Ingeniería: Estática. Addison Wesley.
- Figueroa, D. (2005). Serie: Física para Ciencias e Ingeniería. Volumen 1. Cinemática. Editado por Douglas Figueroa (USB).
- Giambattista, A. 2010. Physics. 2nd. Ed. McGraw Hill.
- Sears, Zemansky. 2016. University Physics with Modern Physics. 14th. Ed. Volume 1.
