Ángulos complementarios: cuáles y cómo se calculan, ejemplos, ejercicios
Dos o más ángulos son ángulos complementarios si la suma de sus medidas se corresponde con la de un ángulo recto. Como se sabe, la medida de un ángulo recto en grados es 90º, y en radianes es π/2.

Por ejemplo, los dos ángulos adyacentes a la hipotenusa de un triángulo rectángulo son complementarios entre sí, ya que la suma de sus medidas es 90º. La siguiente figura es muy ilustrativa al respecto:
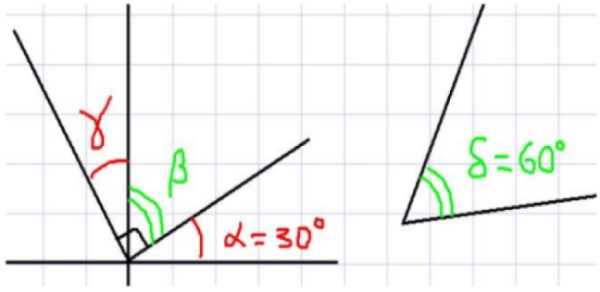
En la figura 1 se muestra un total de cuatro ángulos. α y β son complementarios ya que son adyacentes y su suma completa un ángulo recto. Similarmente β es complementario de γ, de donde se deduce que γ y α son de igual medida.
Ahora bien, como la suma de α y δ es igual a 90 grados, puede afirmarse que α y δ son complementarios. Además, como β y δ tienen un mismo complementario α, puede afirmarse que β y δ tienen la misma medida.
Índice del artículo
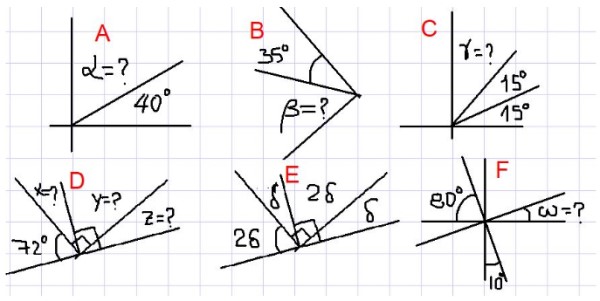
En los ejemplos siguientes se pide encontrar los ángulos desconocidos, señalados con interrogación en la figura 2.
Los siguientes ejemplos van en orden de complejidad.
Ejemplo A
En la figura superior tenemos que los ángulos adyacentes α y 40º suman un ángulo recto. Es decir α + 40º = 90º, por lo tanto α = 90º- 40º = 50º.
Ejemplo B
Como β es complementario con el ángulo de 35º, entonces β = 90º – 35º = 55º.
Ejemplo C
De la figura 2C se tiene que la suma de γ + 15º + 15º = 90º. Es decir que γ es complementario con el ángulo 30º = 15º + 15º. De manera que:
γ = 90º- 30º = 60º
En estos ejemplos hay más ángulos involucrados. Para hallar las incógnitas, el lector debe aplicar el concepto de ángulo complementario tantas veces como sea necesario.
Ejemplo D
Como X es complementario con 72º, se deduce que X = 90º – 72º = 18º. Además Y es complementario con X, entonces Y = 90º – 18º = 72º.
Por último Z es complementario con Y. De todo lo anterior se deduce que:
Z = 90º – 72º = 18º
Ejemplo E
Los ángulos δ y 2δ son complementarios, por lo tanto δ + 2δ = 90º.
Es decir 3δ = 90º, lo que implica que δ = 90º / 3 = 30º.
Ejemplo F
Si llamamos U al ángulo que está entre ω y el de 10º se tiene entonces que U es suplementario a ellos dos, porque se observa que su suma completa un ángulo recto. De donde se deduce que U = 80º. Como U es complementario con ω, entonces ω = 10º.
A continuación se proponen tres ejercicios. En todos ellos debe encontrarse el valor de los ángulos A y B en grados, de modo que se cumplan las relaciones mostradas en la figura 3.
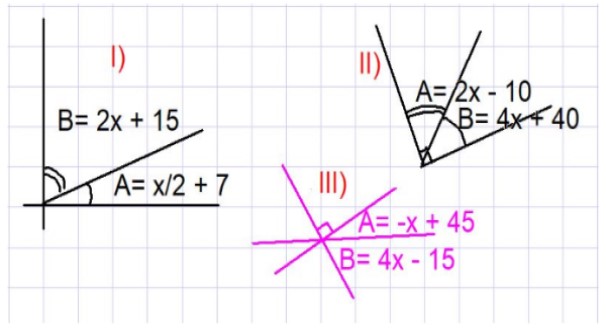
Determine los valores de los ángulos A y B de la parte I) de la figura 3.
Solución
De la figura mostrada se ve que A y B son complementarios, por lo tanto A + B = 90º. Se sustituye la expresión de A y de B como función de x dada en la parte I):
(x/2 + 7) + (2x + 15) = 90
Seguidamente se agrupan los términos apropiadamente y se obtiene una ecuación lineal sencilla:
(5x/2) + 22 = 90
Restando 22 en ambos miembros se tiene:
5x/2 = 90 -22 = 68
Y por último se despeja el valor de x:
x = 2*68/5 = 136/5
Ahora se encuentra el ángulo A sustituyendo el valor de X:
A= (136/5)/2 +7 = 103/5 = 20,6 º.
Mientras que el ángulo B es:
B= 2*136/5 + 15 = 347/5º = 69,4º .
Halle los valores de los ángulos A y B de imagen II, figura 3.
Solución
Nuevamente, como A y B son ángulos complementarios se tiene que: A + B = 90º. Sustituyendo la expresión de A y de B como función de x dada en la parte II) de la figura 3 se tiene:
(2x – 10) + (4x +40) = 90
Se agrupan los términos semejantes para obtener la ecuación:
6 x + 30 = 90
Dividiendo ambos miembros entre 6 se obtiene:
x + 5 = 15
De donde se deduce que x= 10º.
Por lo tanto:
A = 2*10 – 10 = 10º
B = 4*10 + 40 = 80º.
Determine los valores de los ángulos A y B de la parte III) de la figura 3.
Solución
Otra vez se analiza la figura cuidadosamente para buscar los ángulos complementarios. En este caso se tiene que A + B = 90 grados. Sustituyendo la expresión de A y de B como función de x dada en la figura, se tiene:
(-x +45) + (4x -15) = 90
3 x + 30 = 90
Dividiendo ambos miembros entre 3 resulta lo siguiente:
x + 10 = 30
De donde se deduce que x=20º.
Es decir que el ángulo A =-20 +45 = 25º. Y por su parte: B = 4*20 -15 = 65º.
Se dice que dos ángulos son de lados perpendiculares si cada lado tiene su correspondiente perpendicular en el otro. La siguiente figura aclara el concepto:
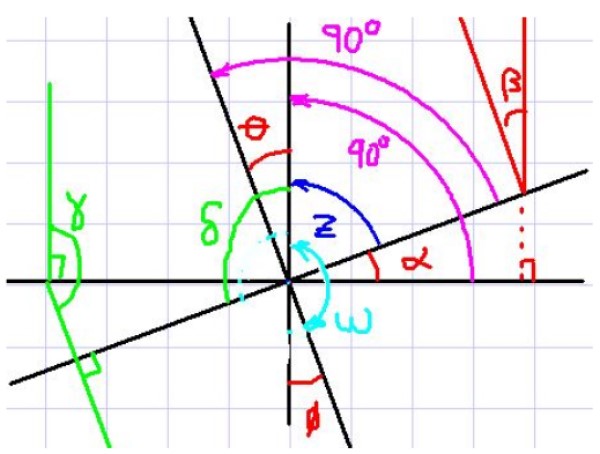
En la figura 4 se observan los ángulos α y θ, por ejemplo. Ahora nótese que cada ángulo tiene su correspondiente perpendicular en el otro ángulo.
También se ve que α y θ tienen el mismo ángulo complementario z, por lo tanto el observador concluye de inmediato que α y θ tienen la misma medida. Pareciera entonces que si dos ángulos tienen lados perpendiculares entre sí, son iguales, pero veamos otro caso.
Ahora considere los ángulos α y ω. Estos dos ángulos también tienen lados correspondientes perpendiculares, sin embargo no puede decirse que sean de igual medida, ya que uno es agudo y el otro es obtuso.
Nótese que ω + θ = 180º. Además θ = α. Si sustituye esta expresión de z en la primera ecuación se obtiene:
δ + α = 180º, siendo que δ y α son ángulos de lados mutuamente perpendiculares.
De lo antes dicho, se puede establecer una regla que se cumple siempre que los ángulos tengan lados perpendiculares:
Si dos ángulos son de lados mutuamente perpendiculares, entonces son iguales si ambos son agudos o ambos son obtusos. De lo contrario, si uno es agudo y el otro es obtuso, entonces son suplementarios, es decir que suman 180º.
Aplicando esta regla y en referencia a los ángulos de la figura 4 podemos afirmar lo siguiente:
α = β = θ = φ
γ = δ
Con el ángulo ω suplementario de α, β, θ y φ.
- Baldor, J. A. 1973. Geometría plana y del espacio. Cultural Centroamericana.
- Leyes y fórmulas matemáticas. Sistemas de medida de ángulos. Recuperado de: ingemecanica.com.
- Wentworth, G. Plane Geometry. Recuperado de: gutenberg.org.
- Wikipedia. Ángulos complementarios. Recuperado de: es.wikipedia.com
- Wikipedia. Transportador. Recuperado de: es.wikipedia.com
- Zapata F. Goniómetro: historia, partes, funcionamiento. Recuperado de: lifeder.com
