Circuitos de corriente alterna: tipos, aplicaciones, ejemplos
Los circuitos de corriente alterna o circuitos ca consisten en combinaciones de elementos resistivos, inductivos y capacitivos, combinados con una fuente de voltaje alterno, que por lo general es sinusoidal.
Al aplicar el voltaje, se establece una corriente variable durante un breve tiempo, llamada corriente transitoria, la cual da paso a la corriente estacionaria sinusoidal.
La corriente sinusoidal tiene valores que se alternan entre positivos y negativos, cambiando a intervalos regulares determinados por una frecuencia previamente establecida. La forma de la corriente se expresa como:
I (t) = Im sen (ωt−φ)
Donde Im es la corriente máxima o amplitud de corriente, ω es la frecuencia, t es el tiempo y φ la diferencia de fase. Las unidades comúnmente empleadas para la corriente son el amperio (A) y sus submúltiplos, como el miliamperio y el microamperio.
Por su parte, el tiempo se mide en segundos, para la frecuencia están los hertzios o Hertz, abreviados Hz, mientras que la diferencia de fase es un ángulo que generalmente se mide en radianes, aunque también a veces se da en grados. Ni estos ni los radianes se consideran unidades.

Con frecuencia el voltaje alterno se simboliza con la onda dentro del círculo, para diferenciarlo del voltaje directo, simbolizado por las dos líneas desiguales y paralelas.
Índice del artículo
- 1 Tipos de circuitos de corriente alterna
- 2 Aplicaciones
- 3 Ejemplos de circuitos de corriente alterna
- 4 Ejercicio resuelto
- 5 Temas de interés
- 6 Referencias
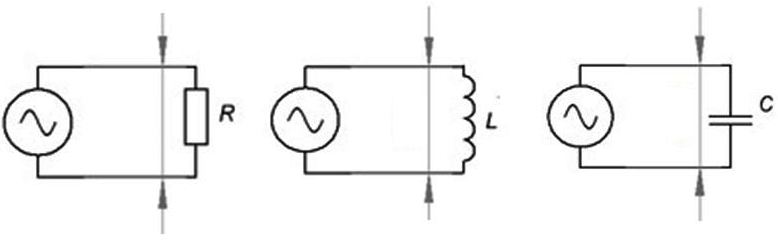
Hay muchas clases de circuitos de corriente alterna, comenzando por los circuitos más sencillos mostrados en la siguiente figura. De izquierda a derecha se tienen:
-Circuito con resistencia R
-Circuito con bobina L
-Circuito con condensador C.
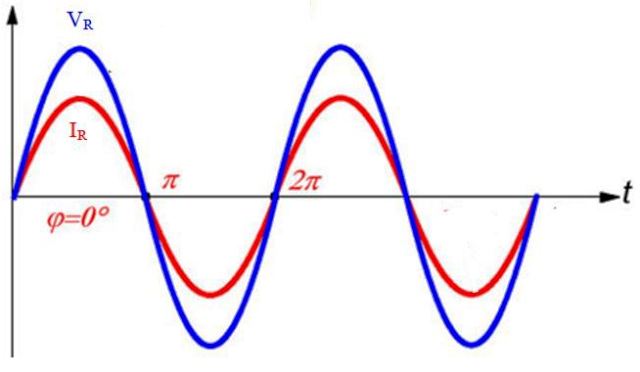
En el circuito con una resistencia R conectada a una fuente de voltaje alterno, el voltaje en la resistencia es VR = Vm sen ωt. Por ley de Ohm, que también es válida para los circuitos puramente resistivos de corriente alterna:
VR = IR∙R
Por lo tanto la corriente máxima Im = Vm /R.
Tanto la corriente como el voltaje se encuentran en fase, lo que significa que alcanzan sus valores máximos, así como el 0, al mismo tiempo.
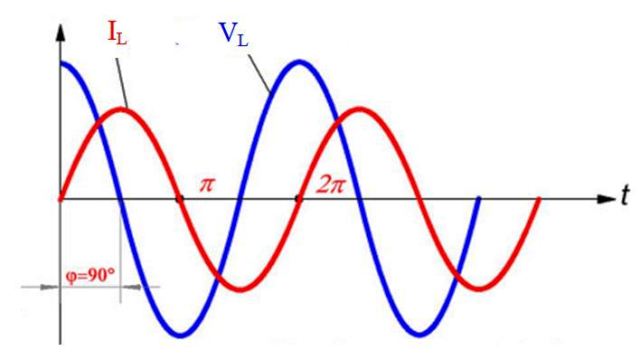
En la bobina L, el voltaje es VL = Vm sen ωt y se relaciona con la corriente en el inductor mediante la ecuación:
Integrando:
Por propiedades de las razones trigonométricas, IL se escribe en términos de sen ωt como:
IL = Im sen (ωt − ½ π)
Entonces, el voltaje y la corriente están desfasados, esta última retrasada ½ π = 90º respecto al voltaje (la corriente comienza antes, siendo t = 0 s el punto de partida). Esto se ve en la siguiente figura que compara la sinusoide de IL y la de VL:
Reactancia inductiva
La reactancia inductiva se define como XL = ωL, aumenta con la frecuencia y tiene dimensiones de resistencia, por lo tanto, en analogía con la ley de Ohm:
VL = IL ∙XL
Para un condensador C conectado a una fuente de corriente alterna, se cumple que:
Q = C ∙VC = C∙Vm sen ωt
La corriente en el condensador se encuentra derivando la carga respecto al tiempo:
IC= ωC∙Vm cos ωt
Pero cos ωt = sen (ωt + ½ π), entonces:
IC = ωCVm sen (ωt+ ½ π)
En este caso, la corriente adelanta al voltaje en ½ π, como se puede ver del gráfico.
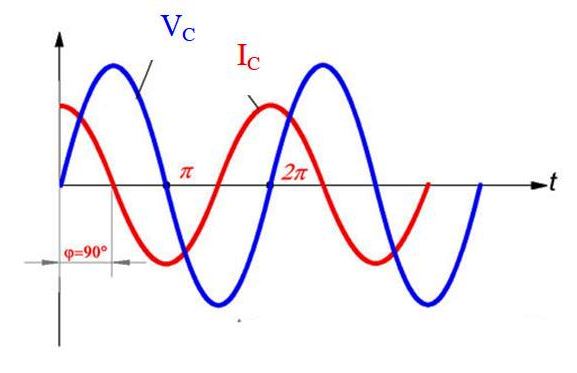
Reactancia capacitiva
La reactancia capacitiva se puede escribir XC = 1/ωC, disminuye con la frecuencia y también tiene unidades de resistencia, es decir, ohmios. De esta manera, la ley de Ohm queda así:
VC = XC.IC
Michael Faraday (1791-1867) fue el primero en obtener una corriente que cambiaba periódicamente su sentido, a través de sus experimentos de inducción, aunque durante los primeros tiempos, solamente se empleaba la corriente directa.
A finales del siglo XIX ocurrió la conocida guerra de las corrientes, entre Thomas A. Edison, defensor del uso de la corriente directa y George Westinghouse, partidario de la corriente alterna. Finalmente esta fue la que ganó por economía, eficiencia y facilidad de transmisión con pérdidas menores.
Por tal motivo hasta la fecha, la corriente que llega a hogares e industrias es corriente alterna, aunque el uso de la corriente directa nunca desapareció del todo.
La corriente alterna se usa para casi todo, y en muchas aplicaciones, el constante cambio de sentido de la corriente alterna no es relevante, como por ejemplo las bombillas de luz, la plancha o la hornilla para cocinar, ya que el calentamiento del elemento resistivo no depende de la dirección del movimiento de las cargas.
En cambio, el hecho de que la corriente cambie de sentido con una determinada frecuencia es el fundamento de los motores eléctricos y diversas aplicaciones más específicas, como las siguientes:
Los circuitos que consisten en una fuente alterna conectada a una resistencia y un condensador en serie, se conocen como circuitos RC serie y se usan para eliminar desfasajes no deseados en otro circuito, o también agregar a este algún efecto especial.
También sirven como divisores de tensión y para sintonizar estaciones de radio (ver el ejemplo 1 en el siguiente apartado).
Los circuitos de tipo puente alimentados con corriente alterna, se pueden usar para medir capacidad o inductancia, del mismo modo que se usa el puente de Wheatstone, un conocido circuito de corriente directa capaz de medir el valor de una resistencia desconocida.
En los apartados anteriores se describieron los circuitos de corriente alterna más simples, aunque desde luego, los elementos básicos antes descritos, así como otros un poco más complejos como diodos, amplificadores y transistores, por nombrar algunos, se pueden combinar para obtener diversos efectos.
Uno de los circuitos más comunes en ca es el que incluye una resistencia R, una bobina o inductor L y un capacitor o condensador C puestos en serie con una fuente de corriente alterna.
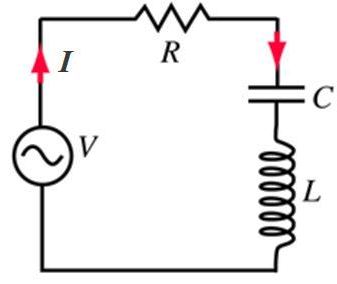
Los circuitos RLC serie responden de manera particular a la frecuencia de la fuente alterna con que se los alimenta. Por eso una de las aplicaciones más interesantes es como circuitos sintonizadores de radio.
Una señal de radio con frecuencia ω genera una corriente con esa misma frecuencia en un circuito especialmente diseñado para que sirva como receptor, y la amplitud de esta corriente es máxima si el receptor se sintoniza con esa frecuencia, a través de un efecto llamado resonancia.
El circuito receptor sirve como sintonizador porque se diseña para que las señales de las frecuencias no deseadas generen corrientes muy pequeñas, las cuales no son detectadas por los parlantes del radio y por lo tanto no son audibles. En cambio, a la frecuencia de resonancia, la amplitud de la corriente llega a un máximo y entonces la señal se escucha claramente.
La frecuencia de resonancia ocurre cuando las reactancias inductiva y capacitiva del circuito se igualan:
XL = XC
1/ωC =ωL
ω2 = 1/LC
La emisora de radio con la señal de frecuencia ω se dice que está “sintonizada”, y los valores de L y C se escogen para esa determinada frecuencia.
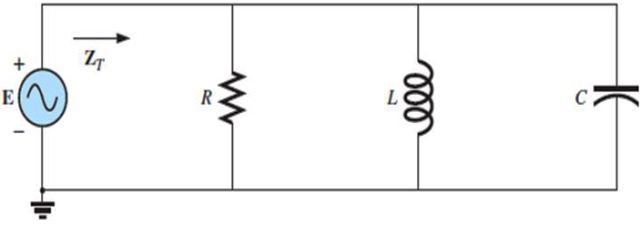
Los circuitos RLC en paralelo también poseen determinadas respuestas según la frecuencia de la fuente, misma que depende de la reactancia de cada uno de los elementos, definida como la razón entre el voltaje y la corriente.
En el circuito LRC en serie del ejemplo 1 de la sección precedente, la resistencia vale 200 ohm, la inductancia 0.4 H y el condensador es de 6 μF. Por su parte, la fuente de alimentación es un voltaje alterno de amplitud igual a 30 V, con frecuencia de 250 rad/s. Se pide encontrar:
a) Las reactancias de cada elemento
b) El valor del módulo de la impedancia del circuito.
c) La amplitud de la corriente
Las respectivas reactancias se calculan con las fórmulas:
XC = 1/ωC = 1 / (250 rad/s x 6 x10-6 F) = 666,67 ohm
XL = ωL = 250 rad/s x 0.4 H = 100 ohm
Y la reactancia de la resistencia equivale a su valor en ohms:
XR = R = 200 ohm
La impedancia Z se define como la razón entre el voltaje y la corriente en el circuito, ya sea en serie o en paralelo:
Z = Vm / Im
La impedancia se mide en ohmios, lo mismo que una resistencia o una reactancia, pero se refiere a la oposición al paso de la corriente de las inductancias y los condensadores, considerando que además de sus efectos particulares, como atrasar o adelantar al voltaje, también tienen una cierta resistencia interna.
Se puede demostrar que para el circuito RLC serie, el módulo de la impedancia viene dada por:
Al evaluar los valores dados en el enunciado, se obtiene:
De:
Z = Vm / Im
Se tiene que;
Im = Vm / Z = 30V / 601 ohms = 0.05 A.
Diferencias entre corriente alterna y directa
- Alexander, C. 2006. Fundamentos de Circuitos Eléctricos. 3ra. Edición. Mc Graw Hill.
- Boylestad, R. 2011. Introducción al Análisis de Circuitos.2da. Edición. Pearson.
- Figueroa, D. (2005). Serie: Física para Ciencias e Ingeniería. Volumen 6. Electromagnetismo. Editado por Douglas Figueroa (USB).
- Sears, Zemansky. 2016. University Physics with Modern Physics. 14th. Ed. Volume 1. Pearson.
- Serway, R., Jewett, J. (2008). Física para Ciencias e Ingeniería. Volumen 1. 7ma. Ed. Cengage Learning.
