Números negativos: concepto, ejemplos, operaciones
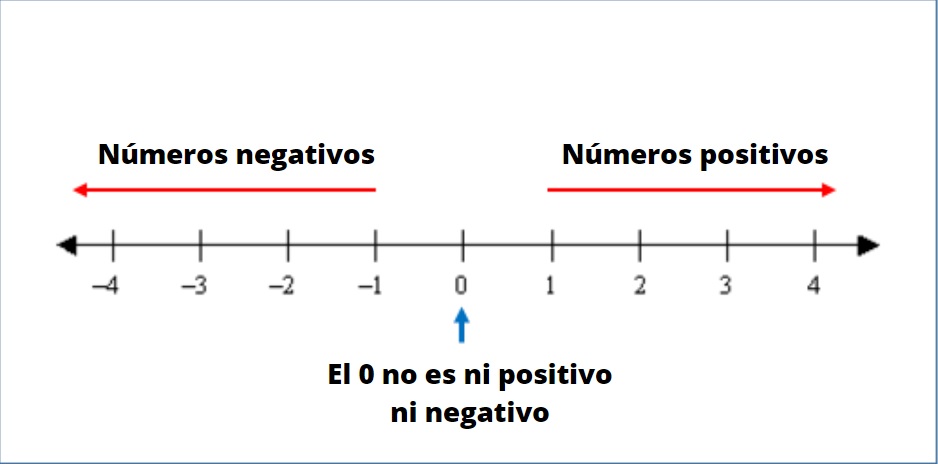
Los números negativos son los que se encuentran a la izquierda de la recta numérica, precedidos siempre de un signo -. Mediante los negativos es posible representar cantidades que se encuentran por debajo o a la izquierda del 0.
Estos números participan activamente de la vida cotidiana: por ejemplo si alguien tiene una deuda de 5 $, pero solo puede pagar 3 $, debe 2 $. La deuda se denota con signo negativo para distinguirla de la suma abonada.
Posiciones bajo nivel del mar, temperaturas por debajo del punto de congelación del agua y pisos inferiores al nivel de la calle se pueden denotar mediante números negativos.
Índice del artículo
La existencia de los negativos extiende las operaciones numéricas posibles. Pongamos el ejemplo de la resta de dos números. Si estos números pertenecen a los naturales 1, 2, 3, 4, 5… la resta solamente tiene sentido si se hace restando a otro número menor que él.
El resultado de la operación 10 – 7 = 3 es razonable, ya que en principio no podemos quitarle a una cantidad más de lo que ella representa.
Sin embargo, con los negativos se describiría bien esta otra situación: queremos comprar algo que vale 20 $, pero solamente tenemos 15 $ y pedimos prestados 5 $ a un amigo. La deuda, como hemos dicho, se marca con signo negativo y así 15 – 20 = -5, el cual se lee como “menos 5”.
El conjunto de los números enteros negativos unido al de los naturales y al 0, conforman el conjunto más amplio de los números enteros Z.
Pero los negativos también pueden ser fraccionarios o decimales y pertenecer a un conjunto todavía más amplio: el de los números reales R, que incluye a los racionales y a los irracionales.
Con todos ellos se llevan a cabo las operaciones aritméticas conocidas, teniendo precaución de operar siguiendo unas reglas sencillas de signos que se explican a continuación.
Antes de realizar operaciones con números negativos, hay que establecer algunas reglas sencillas para manejar el signo (–) que se les debe anteponer siempre y el orden de los números.
Consideremos la recta numérica mostrada en la figura, con los negativos a la izquierda del 0 y los positivos a la derecha.
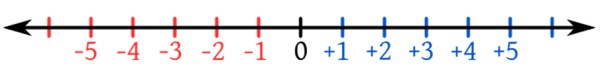
Las flechas de la recta numérica en ambas direcciones indican que existen infinitos números. Obsérvese también que el conjunto numérico de los enteros es un conjunto ordenado y cualquier número negativo es menor que el 0 y que cualquier positivo.
Así, -4 es menor que 1, y -540 es menor que 84, por ejemplo.
La distancia que hay entre cualquier número y el 0 se denomina valor absoluto. Esta distancia siempre es positiva y se denota mediante barras verticales, de esta forma:
│-5│= 5
│+√6│= √6
│-3/4│= 3/4
│-10.2│= 10.2
Es decir, el valor absoluto de cualquier número, ya sea positivo o negativo es el positivo del número. Este concepto nos servirá para más adelante al operar con los números negativos.
Otro detalle muy importante es la distinción entre el signo del número y el signo de la operación.
Cuando un número es positivo por lo general se omite el signo del número y se entiende que es positivo de todas formas, pero con los negativos eso no es posible, por lo tanto es preciso usar paréntesis, veamos:
-Correcto: 17 – (–6) o también +17 – (–6)
-Incorrecto: 17 – –6
-Incorrecto: -5 + +7
-Correcto: – 5 + (+7) o también -5 + 7
Una vez claros los conceptos de valor absoluto, orden e importancia del signo negativo, podemos pasar a las operaciones elementales.
Distinguimos los siguientes casos, comenzando con la suma de dos positivos, cuyo procedimiento ya es muy familiar:
–Sumar dos números positivos: (+a) + (+b) = a + b
Lo cual significa que sumamos como de costumbre, veamos:
(+8) + (+5) = 8 + 5 = 13
–Sumar dos números negativos: (-a) + (-b) = – (a + b)
En este caso sumamos los valores absolutos de los números y al resultado se antepone un signo negativo, así:
(-7) + (-11) = – (7+ 11) = – 18
–Sumar un negativo y un positivo: (+a) + (-b)
Para esta operación, los valores absolutos se restan y el resultado lleva el signo del número con mayor valor absoluto. Hagamos algunos casos:
a) (-16) + (+3)
Los respectivos valores absolutos son 16 y 3, el número con mayor valor absoluto es 16, cuyo signo es negativo, entonces:
(-16) + (+3) = – (16 – 3) = -13
b) (+8) + (-3) = + (8-3) = +5 = 5
La suma de negativos también es conmutativa, lo que quiere decir que el orden en los sumandos no es importante para el resultado.
Las reglas anteriores aplican si se quiere sumar más de dos números, lo cual se puede hacer con la propiedad asociativa: a+b + c = (a +b) + c = a + (b+c).
Antes de ver un ejemplo en este caso, veamos primero la resta de dos números enteros.
La resta se define como la suma del opuesto. El opuesto a un número a es –a, así:
-4 es el opuesto de + 4
½ es el opuesto de -½
Si nos piden llevar a cabo la resta de dos números, independientemente del signo, simplemente al primero le sumamos el opuesto del segundo:
a) (-53) – (+8) = (-53) + (-8) = – (53+8) = -61
b) (+7) – (-12) = (+7) + (+12) = 7+12 = 19
c) (+2) – (+π) = (+2) + (-π) = 2 – π
Ejemplo
Efectuar la siguiente operación (+4) + (-7) + (+19)
Lo reescribimos así con ayuda de corchetes para indicar la operación que se va a realizar primero:
(+4) + (-7) + (+19) = [(+4) + (-7)] + (+19) = [- (4 -7)] + 19 = [- (-3)] + 19 = 19 – (-3) = 19 + (+3) = 22
La regla de los signos para la multiplicación se resume en la siguiente figura:
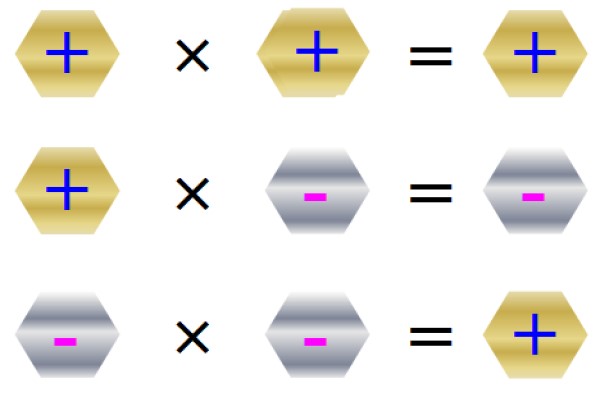
Propiedades de la multiplicación
-Conmutatividad: el orden de los factores no altera el producto, por lo tanto ≠ = b.a donde a y b son números negativos, enteros o fraccionarios.
–Asociatividad: sean a, b y c números enteros, se cumple que (a.b). c = a. (b.c)
–Distributividad respecto a la suma: sean a, b y c números enteros, es válido que a. (b+c) = a.b +a.c
Ejemplo
(-3/2) x [(-5) + (+4) – (+2)] = (-3/2) x (-5) + (-3/2) x (+4) + (-3/2) x (-2) = (15 – 12 + 6)/2 = 9/2
También se pudo haber resuelto primero la operación entre corchetes y al resultado multiplicarlo por (-3/2), así:
(-3/2) x [-5 + 4 – 2] = (-3/2) x (-3) = 9/2
La regla de los signos para la división se expone en la siguiente figura:
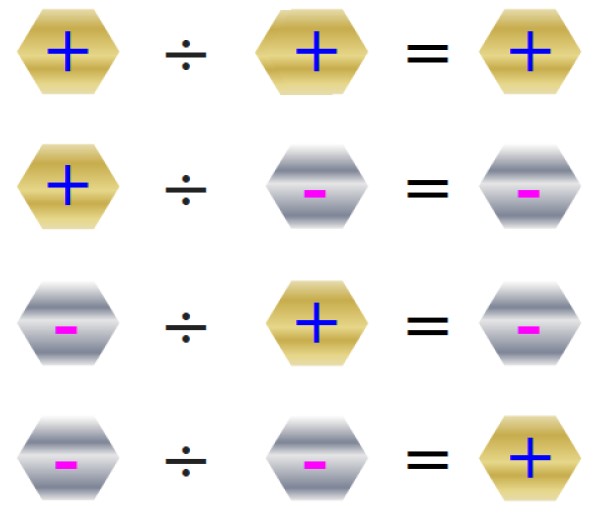
La división no es conmutativa y por lo general a ÷ b ≠ b ÷ a, no siendo permitida la división entre 0. Veamos un ejemplo:
(-54) ÷ (+3) = -18
Para obtener este resultado simplemente se hace el cociente y el signo se escoge de acuerdo a la tabla mostrada en la figura, que corresponde a la tercera opción de arriba abajo.
La potenciación es la operación de la forma an, donde a es la base y n es el exponente. La base y el exponente pueden tener cualquier signo.
-Si la base es negativa o positiva y el exponente es entero par, el resultado de la operación siempre es positivo.
-Cuando la base es positiva y el exponente es entero impar el resultado es positivo.
-Y si la base es negativa y el exponente es entero impar, el resultado es negativo.
Los exponentes fraccionarios se expresar alternativamente como raíz, por ejemplo una raíz cuadrada equivale al exponente fraccionario ½, una raíz cúbica equivale al exponente 1/3 y así sucesivamente.
Veamos algunos ejemplos:
a) (-3)3 = (-3) x (-3) x (-3) = -27
b) 16 -1/2 = 1 / √16 = ¼
c) (+8) 1/3 = raíz cúbica de 8 = 2
- Baldor, A. 1986. Aritmética. Ediciones y Distribuciones Códice.
- Figuera, J. 2000. Matemática 7mo. Grado. ediciones CO-BO.
- Jiménez, R. 2008. Álgebra. Prentice Hall.
- Math is fun. How to Add and Subtract Positive and Negative Numbers. Recuperado de: mathisfun.com
- Wikipedia. Números negativos. Recuperado de: es.wikipedia.org.
