Método húngaro: en qué consiste, ejemplo
El método húngaro es un algoritmo que se utiliza en problemas de asignación cuando se quiere minimizar el costo. Es decir, se usa para encontrar el costo mínimo al asignar varias personas a diversas actividades basadas en el menor costo. Se debe asignar cada actividad a una persona diferente.
Un problema de asignación es un tipo especial de problema de programación lineal, donde el objetivo es minimizar el costo o el tiempo de completar una cantidad de trabajos por parte de varias personas.

Una de las características importantes del problema de asignación es que solo se asigna un trabajo (o trabajador) a una máquina (o proyecto).
Este método fue desarrollado por el matemático húngaro D. Konig. Por esta razón, se le conoce como el método húngaro para problemas de asignación. También es conocido como algoritmo de asignación de Kuhn-Munkres.
Cualquier problema de asignación se puede resolver fácilmente aplicando este método que consta de dos fases:
– Con la primera fase se realizan reducciones de filas y reducciones de columnas.
– En la segunda fase se optimiza la solución sobre una base iterativa.
Índice del artículo
El método húngaro consta de cuatro pasos. Los primeros dos pasos se ejecutan una sola vez, mientras que los pasos 3 y 4 se repiten hasta encontrar una asignación óptima.
Se considera como dato de entrada a una matriz cuadrada del orden n por n, la cual debe contener solamente elementos no negativos.
Para un problema dado, si el número de filas de la matriz no es igual al número de columnas se debe agregar una fila ficticia o una columna ficticia, dependiendo del caso. Los costos de asignación para esas celdas ficticias siempre se asignan como cero.
Para cada fila de la matriz se selecciona el elemento con el valor más bajo y se lo resta de cada elemento en esa fila.
De manera similar, se selecciona para cada columna el elemento con el valor más bajo y se lo resta de cada elemento en esa columna.
Se deben cubrir todos los ceros en la matriz resultante del paso 2 usando un número mínimo de líneas horizontales y verticales, ya sea por filas o columnas.
Si se requiere un total de n líneas para cubrir todos los ceros, siendo n igual al tamaño n por n de la matriz, se tendrá una asignación óptima entre los ceros y por tanto el algoritmo se detiene.
De lo contrario, si se requieren menos de n líneas para cubrir todos los ceros en la matriz, se continúa con el paso 4.
Se selecciona el menor elemento de la matriz (llamado k) que no esté cubierto por una de las líneas realizadas en el paso 3.
Se resta el valor de k de todos los elementos que no están cubiertos por líneas. Posteriormente se suma el valor de k a todos los elementos que están cubiertos por la intersección de dos líneas.
Los elementos que están cubiertos por una sola línea se dejan tal como están. Después de realizar este paso, se regresa al paso 3.
Una vez que se detenga el algoritmo en el paso 3, se elige un conjunto de ceros de tal manera que cada fila y cada columna tenga solo un cero seleccionado.
Si en este proceso de selección no existe un único cero en una fila o columna, se elegirá entonces uno de esos ceros. Se eliminan los ceros restantes en esa columna o fila, repitiendo lo mismo para las otras asignaciones también.
Si no hay una única asignación de ceros significa que existen múltiples soluciones. Sin embargo, el costo seguirá siendo el mismo para los diferentes conjuntos de asignaciones.
Se elimina cualquier fila o columna ficticia que se haya agregado. Los ceros elegidos en esta matriz final corresponden así a la asignación ideal requerida en la matriz original.
Consideremos una empresa donde existen cuatro actividades (A1, A2, A3, A4) que deben ser ejecutadas por cuatro trabajadores (T1, T2, T3, T4). Se debe asignar una actividad por trabajador.
La siguiente matriz muestra el costo de asignar un determinado trabajador a una determinada actividad. El objetivo que se persigue es minimizar el costo total de la tarea compuesta por estas cuatro actividades.
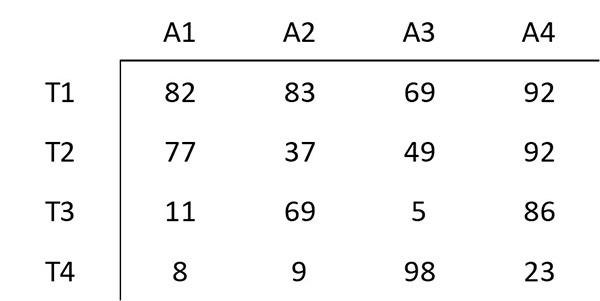
Se comienza por restar el elemento con el valor mínimo de cada fila de los demás elementos de esa fila. Por ejemplo, el elemento más pequeño en la primera fila es 69. Por tanto, se resta 69 de cada elemento en la primera fila. La matriz resultante es:
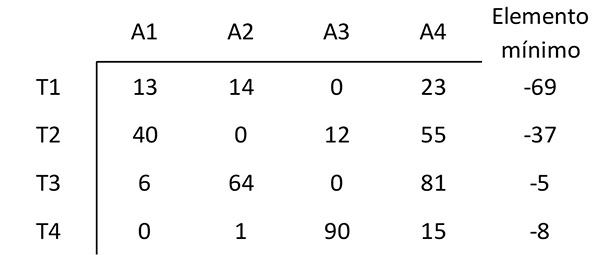
Del mismo modo, se resta el elemento con el valor mínimo de cada columna de los demás elementos de esa columna, obteniendo la siguiente matriz:
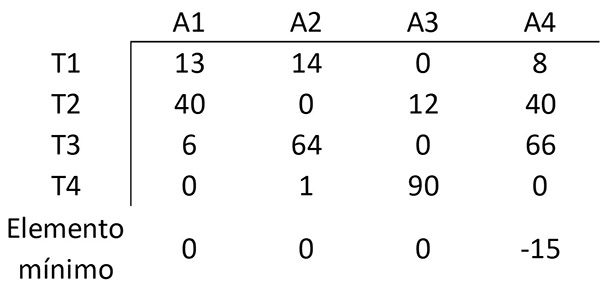
Ahora se determinará el mínimo número de líneas (horizontales o verticales) que se requieren para cubrir todos los ceros en la matriz. Todos los ceros se pueden cubrir usando 3 líneas:
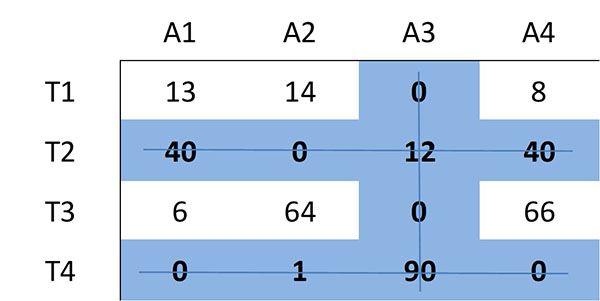
Debido a que el número de líneas requeridas es tres y es menor que el tamaño de la matriz (n=4), se continúa con el paso 4.
Se selecciona el menor elemento no cubierto por las líneas, cuyo valor es 6. Se resta este valor de todos los elementos no cubiertos y este mismo valor se suma a todos los elementos cubiertos por la intersección de dos líneas. Esto da como resultado la siguiente matriz:
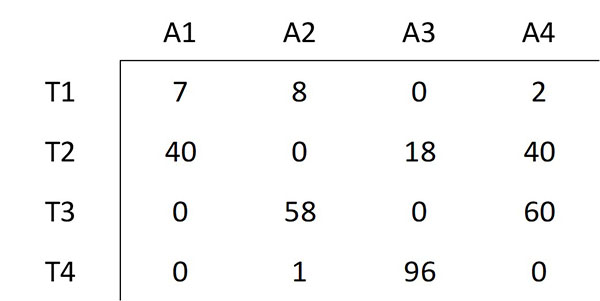
Tal como está indicado en el método húngaro, se debe realizar de nuevo el paso número tres.
Nuevamente se determina el mínimo número de líneas requeridas para cubrir todos los ceros en la matriz. En esta ocasión se requieren cuatro líneas:
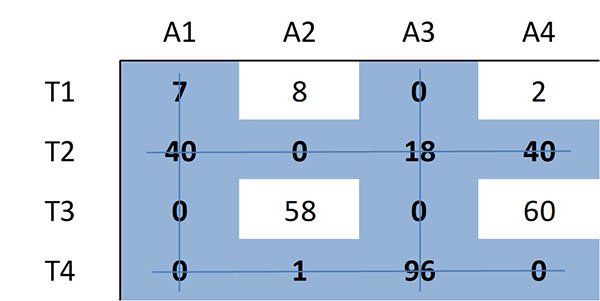
Debido a que el número de líneas requeridas es 4, igual al tamaño de la matriz (n=4), se tiene una asignación óptima entre los ceros en la matriz. Por tanto, el algoritmo se detiene.
Tal como indica el método, la selección realizada de los siguientes ceros corresponde a una asignación óptima:
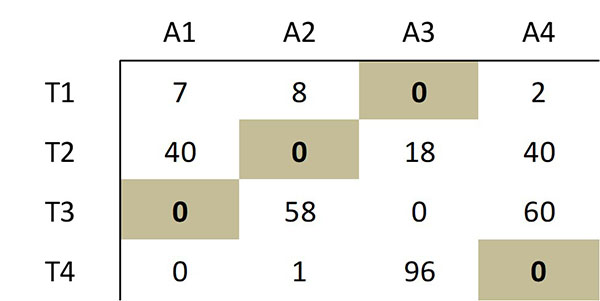
Esta selección de ceros corresponde a la siguiente asignación óptima en la matriz de costos original:
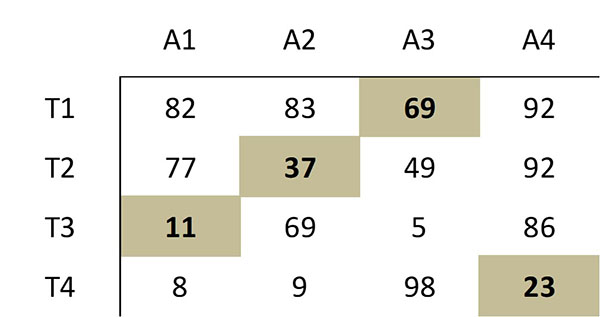
Por tanto, el trabajador 1 debe realizar la actividad 3, el trabajador 2, la actividad 2, el trabajador 3, la actividad 1 y el trabajador 4 debe realizar la actividad 4. El costo total de esta asignación óptima es de 69+37+11+23=140.
- Hungarian Algorithm (2019). The Hungarian algorithm. Tomado de: hungarianalgorithm.com.
- Study (2019). Using the Hungarian Algorithm to Solve Assignment Problems. Tomado de: study.com.
- Wisdom Jobs (2018). Hungarian Method for Solving Assignment Problem – Quantitative Techniques for Management. Tomado de: wisdomjobs.com.
- Geeks for Geeks (2019). Hungarian Algorithm for Assignment Problem. Tomado de: geeksforgeeks.org.
- Karleigh Moore, Nathan Landman (2019). Hungarian Maximum Matching Algorithm. Brilliant. Tomado de: brilliant.org.
