Medidas de tendencia central para datos agrupados: fórmulas, ejercicios

Las medidas de tendenciacentral señalan el valor alrededor del cual están los datos de una distribución. La más conocida es el promedio o media aritmética, que consiste en sumar todos los valores y dividir el resultado entre el número total de datos.

Sin embargo, si la distribución consta de un gran número de valores y no se presentan de un modo ordenado, no resulta fácil realizar los cálculos necesarios para extraer la información valiosa que contienen.

Es por ello que se agrupan en clases o categorías, para elaborar una distribución defrecuencias. Llevando a cabo este ordenamiento previo de los datos, luego es más fácil calcular las medidas de tendencia central, entre las cuales se encuentran:

-Media

-Mediana

-Moda

-Media geométrica

-Media armónica

Fórmulas

A continuación tenemos las fórmulas de las medidas de tendencia central para los datos agrupados:

Media aritmética

La media es la más utilizada para caracterizar datos cuantitativos (valores numéricos), aunque es bastante sensible a los valores extremos de la distribución. Se calcula mediante:

Con:

-X: promedio o  media aritmética

-f_i: frecuencia de la clase

-m_i: la marca de clase

-g: número de clases

-n: total de los datos

Mediana

Para calcularla es necesario hallar el intervalo que contiene la observación n/2 e interpolar para determinar el valor numérico de dicha observación, mediante la siguiente fórmula:

Donde:

-c: ancho del intervalo al que pertenece la mediana

-B_M: frontera inferior de dicho intervalo

-f_m: número de observaciones que contiene el intervalo

-n/2: total de datos dividido entre 2.

-f_BM: cantidad de observaciones que hay antes del intervalo que contiene la mediana.

Por lo tanto, la mediana es una medida de posición, es decir, divide el conjunto de datos en dos partes. También se pueden definir cuartiles, deciles y percentiles, que dividen la distribución en cuatro, diez y cien partes respectivamente.

Moda

En los datos agrupados, se busca la clase o categoría que contiene la mayoría de las observaciones. Esta es la clase modal. Puede que una distribución tenga dos o más modas, en cuyo caso se la denomina bimodal y multimodal, respectivamente.

También se puede calcular la moda en datos agrupados siguiendo la ecuación:

Con:

-L₁: límite inferior de la clase donde se encuentra la moda

-Δ₁: resta entre la frecuencia de la clase modal y la frecuencia de la clase que la precede.

-Δ₂: resta entre la frecuencia de la clase modal y la frecuencia de la clase que le sigue.

-c: ancho del intervalo que contiene la moda

Media armónica

La media armónica se denota mediante H. Cuando se tiene un conjunto de n valores x₁, x₂, x₃…, la media armónica es el inverso o recíproco de la media aritmética de los inversos de los valores.

Es más fácil verlo a través de la fórmula:

Y al disponer de los datos agrupados, la expresión se transforma en:

Donde:

-H: media armónica

-f_i: frecuencia de la clase

-m_i: marca de clase

-g: número de clases

-N = f₁ + f₂ + f₃ + …

Media geométrica

Si se tienen n números positivos x₁, x₂, x₃…, su media geométrica G se calcula mediante la raíz n-ésima del producto de todos los números:

En el caso de los datos agrupados, se puede demostrar que el logaritmo decimal de la media geométrica log G, viene dado por:

Donde:

-G: media geométrica

-f_i: frecuencia de la clase

-m_i: la marca de clase

-g: número de clases

-N = f₁ + f₂ + f₃ + …

Relación entre H, G y X

Siempre se cumple que:

H ≤ G ≤ X

Definiciones más usadas

Las siguientes definiciones son necesarias para encontrar los valores descritos en las fórmulas anteriores:

Frecuencia

La frecuencia se define como el número de veces que se repite un dato.

Rango

Es la diferencia entre el valor mayor y el menor, presentes en la distribución.

Número de clases

Para saber en cuántas clases agrupamos los datos, nos servimos de algún criterio, por ejemplo el siguiente:

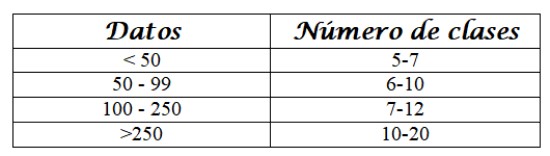
Límites

Los valores extremos de cada clase o intervalo se llaman límites y cada clase puede tener ambos límites bien definidos, en cuyo caso tiene un límite menor y uno mayor. O bien puede tener límites abiertos, cuando se da un rango, por ejemplo de valores mayores o menores a cierto número.

Marca de clase

Consiste simplemente en el punto medio del intervalo y se calcula promediando el límite superior y el límite inferior.

Ancho del intervalo

Los datos se pueden agrupar en clases de igual o diferente tamaño, este es el ancho o amplitud. La primera opción es la más utilizada, pues facilita mucho los cálculos, aunque en algunos casos es imperativo que las clases tengan distinto ancho.

El ancho c del intervalo se puede determinar mediante la siguiente fórmula:

c= Rango / N_c

Donde N_c es el número de clases.

Ejercicio resuelto

A continuación tenemos una serie de mediciones de velocidad en km/h, tomadas con radar, que corresponden a 50 autos que pasaron por una calle de determinada ciudad:

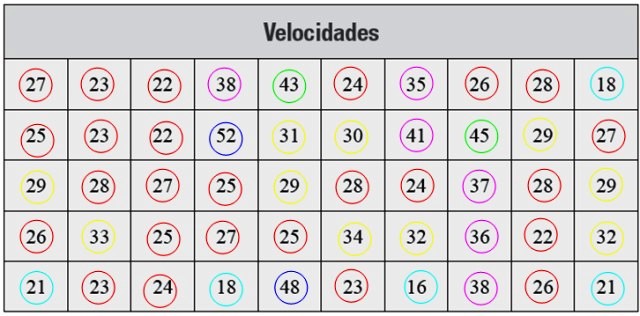
Solución

Los datos así presentados no están organizados, así que el primer paso es agruparlos en clases.

Pasos para agrupar los datos y construir la tabla

Paso 1

Hallar el rango R:

R = (52 – 16) km/h = 36 km/h

Paso 2

Seleccionar el número de clases N_c, de acuerdo al criterio dado. Como hay 50 datos, podemos escoger N_c = 6.

Paso 3

Calcular el ancho c del intervalo:

c = Rango /N_c = 36 / 6 = 6

Paso 4

Formar clases y agrupar datos de la siguiente manera: para la primera clase se escoge como límite inferior un valor apenas menor que el menor valor presente en la tabla, después se le suma a este valor el de c=6, calculado previamente, y se obtiene así el límite superior de la primera clase.

Se procede de la misma manera para construir el resto de las clases, como se muestra en la siguiente tabla:

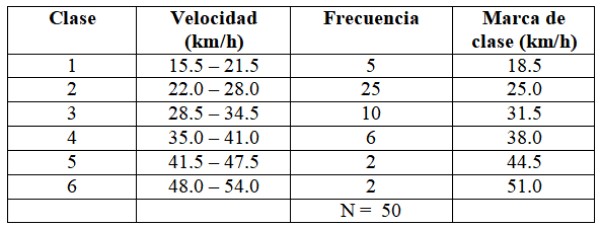
Cada frecuencia corresponde a un color en la figura 2, de esta forma se asegura que ningún valor escape de ser contabilizado.

Cálculo de la media

X = (5 x 18.5 +25 x 25.0 + 10 x 31.5 + 6 x 38.0 + 2 x 44.5 + 2 x 51.0) ÷ 50 = 29.03 km/h

Cálculo de la mediana

La mediana se encuentra en la clase 2 de la tabla, ya que allí están los 30 primeros datos de la distribución.

-Ancho del intervalo al que pertenece la mediana: c=6

-Frontera inferior del intervalo donde está la mediana: B_M = 22.0 km/h

-Número de observaciones que contiene el intervalo f_m =25

-Total de datos dividido entre 2: 50/2 = 25

-Cantidad de observaciones que hay antes del intervalo que contiene la mediana: f_BM = 5

Y la operación es:

Mediana = 22.0 + [(25-5)÷25]×6 = 26.80 km/h

Cálculo de la moda

La moda también se encuentra en la clase 2:

-Ancho del intervalo: c = 6

-Límite inferior de la clase donde se encuentra la moda: L₁ = 22.0

-Resta entre la frecuencia de la clase modal y la frecuencia de la clase que la precede: Δ₁ =25-5= 20

-Resta entre la frecuencia de la clase modal y la frecuencia de la clase que le sigue: Δ₂ = 25 – 10 = 15

Con estos datos la operación es:

Moda = 22.0 + [20 ÷ (20+15)]x6 = 25.4 km/h

Cálculo de la media geométrica

N = f₁ + f₂ + f₃ + … = 50

log G = (5 x log 18.5 + 25 x log 25 + 10 x log 31.5 + 6 x log 38 + 2 × log 44.5 + 2 x log 51) /50 =

log G = 1.44916053

G = 28.13 km/h

Cálculo de la media armónica

1/H = (1/50) x [(5/18.5) + (25/25) + (10/31.5) + (6/38) + (2/44.5) + (2/51)] = 0.0366

H =  27.32 km/h

Resumen de medidas de tendencia central

Las unidades de las variables son km/h:

-Media: 29.03

-Mediana: 26.80

-Moda: 25.40

-Media geométrica: 28.13

-Media armónica: 27.32

Referencias

1. Berenson, M. 1985. Estadística para administración y economía. Interamericana S.A.
2. Canavos, G. 1988. Probabilidad y Estadística: Aplicaciones y métodos. McGraw Hill.
3. Devore, J. 2012. Probability and Statistics for Engineering and Science. 8th. Edition. Cengage.
4. Levin, R. 1988. Estadística para Administradores. 2da. Edición. Prentice Hall.
5. Spiegel, M. 2009. Estadística. Serie Schaum. 4 ta. Edición. McGraw Hill.
6. Tratamiento de datos agrupados. Recuperado de: itchihuahua.edu.mx.
7. Walpole, R. 2007. Probabilidad y Estadística para Ingeniería y Ciencias. Pearson.