Teorema de Bayes: qué es, explicación, aplicaciones, ejercicios
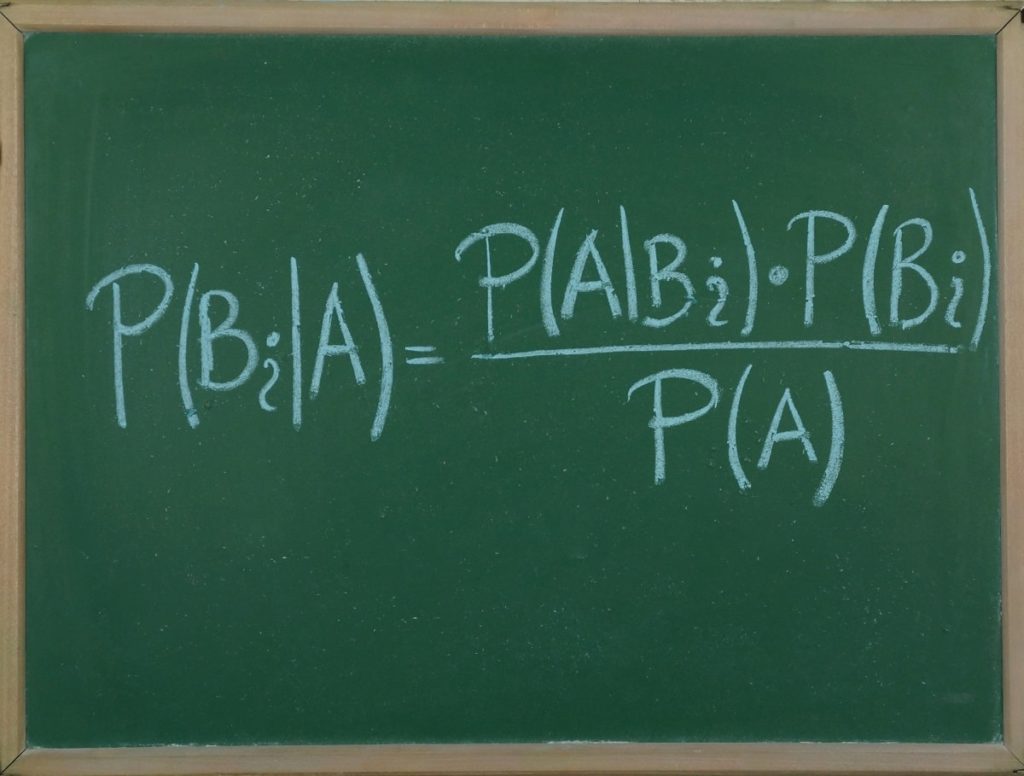
¿Qué es el teorema de Bayes?
El teorema de Bayes es un procedimiento que nos permite expresar la probabilidad condicional de un evento aleatorio A dado B, en términos de la distribución de probabilidad del evento B dado A y la distribución de probabilidad de solo A.
Este teorema es de mucha utilidad, ya que gracias a él podemos relacionar la probabilidad de que un evento A ocurra sabiendo que ocurrió B, con la probabilidad de que ocurra lo contrario, es decir, que ocurra B dado A.
El teorema de Bayes fue una proposición plateada por el reverendo Thomas Bayes, un teólogo inglés del siglo XVIII quien también fue matemático. Fue autor de varios trabajos en teología, pero en la actualidad es conocido por un par de tratados matemáticos, entre los cuales destaca como resultado principal el ya referido teorema de Bayes.
Bayes se ocupó de este teorema en un trabajo titulado “An Essay towards solving a Problem in the Doctrine of Chances” (Un ensayo para resolver un problema en la doctrina de las posibilidades), publicado en 1763, y sobre el cual se han desarrollado grandes estudios con aplicaciones en diversas áreas de conocimiento.
Explicación
Primero, para una mayor compresión de este teorema, son necesarias algunas nociones básicas de teoría de probabilidad, especialmente el teorema de la multiplicación para probabilidad condicional, el cual establece que
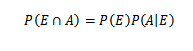
Para E y A eventos arbitrarios de un espacio muestral S.
Y la definición de particiones, la cual nos dice que si tenemos A1 ,A2,…, An eventos de un espacio muestral S, estos formarán una partición de S, si los Ai son mutuamente exclusivos y su unión es S.
Teniendo esto, sea B otro evento. Entonces podemos ver a B como
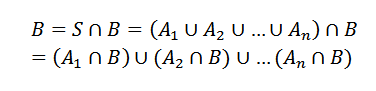
Donde las Ai intersectadas con B son eventos mutuamente exclusivos.
Y en consecuencia,
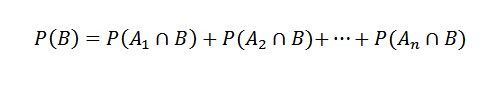
Luego, aplicando el teorema de la multiplicación
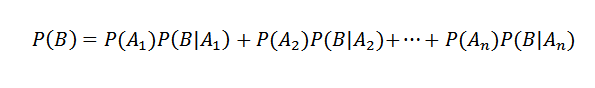
Por otra parte, la probabilidad condicional de Ai dado B se define por
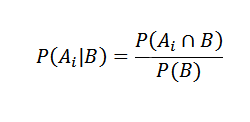
Sustituyendo de manera adecuada tenemos que para cualquier i
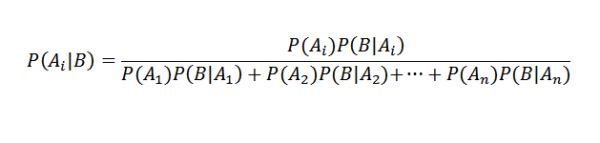
Aplicaciones del teorema de Bayes
Gracias a este resultado, grupos de investigación y corporaciones diversas han logrado mejorar los sistemas que están basados en conocimientos.
Estudio de enfermedades
Por ejemplo, en el estudio de enfermedades, el teorema de Bayes puede ayudar a discernir la probabilidad de que una enfermedad sea encontrada en un grupo de personas con una característica dada, tomando como datos las tasas globales de la enfermedad y el predominio de dicha características en personas tanto sanas como enfermas.
Desarrollo de software
Por otro lado, en el mundo de las altas tecnologías, ha influenciado a grandes compañías que han desarrollado, gracias a este resultado, software “Basados en el Conocimiento”.
Como ejemplo cotidiano tenemos el asistente de Microsoft Office. El teorema de Bayes ayuda al software a evaluar los problemas que presenta el usuario y determinar qué consejo proporcionarle y así poder ofrecer un mejor servicio según los hábitos del usuario.
Cabe destacar que esta fórmula fue ignorada hasta tiempos recientes, esto se debe principalmente a que cuando se desarrolló este resultado hace 200 años, había poco uso práctico para ellos. Sin embargo, en nuestra época, gracias a los grandes avances tecnológicos, los científicos han logrado maneras de poner en práctica este resultado.
Ejercicios resueltos
Ejercicio 1
Una empresa de celulares tiene dos máquinas A y B. El 54% de los celulares producidos son hechos por la máquina A y el resto por la máquina B. No todos los celulares producidos están en buen estado.
La proporción de celulares defectuosos hechos por A es 0.2 y por B es 0.5. ¿Cuál es la probabilidad de que un celular de dicha fábrica sea defectuoso? ¿Cuál es la probabilidad de que, sabiendo que un celular es defectuoso, proceda de la máquina A?
Solución
Aquí, se tiene un experimento que se realiza en dos partes; en la primera parte ocurren los eventos:
A: celular hecho por la máquina A.
B: celular hecho por la máquina B.
Ya que la máquina A produce el 54% de los celulares y el resto los produce la máquina B, se tiene que la máquina B produce el 46% de los celulares. Las probabilidades de estos eventos son dadas, a saber:
P(A)=0,54.
P(B)=0,46.
Los eventos de la segunda parte del experimento son:
D: celular defectuoso.
E: celular no defectuoso.
Como se dice en el enunciado, las probabilidades de estos eventos dependen del resultado obtenido en la primera parte:
P(D|A)=0,2.
P(D|B)=0,5.
Utilizando estos valores, se puede determinar también las probabilidades de los complementos de estos eventos, es decir:
P(E|A) = 1 – P(D|A)
= 1 – 0,2
= 0,8
y
p(E|B) = 1 – P(D|B)
= 1 – 0,5
= 0,5.
Ahora, el evento D se puede escribir como sigue:
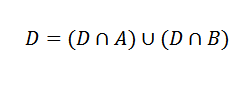
Utilizando el Teorema de la multiplicación para probabilidad condicional resulta:
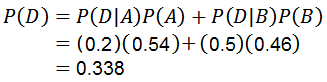
Con lo cual se responde la primera pregunta.
Ahora solo falta calcular P(A|D), para lo cual se aplica el teorema de Bayes:
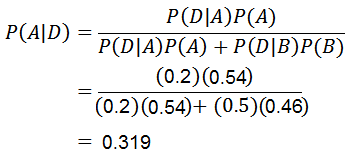
Gracias al teorema de Bayes se puede afirmar que la probabilidad de que un celular haya sido hecho por la máquina A, sabiendo que el celular es defectuoso, es de 0.319.
Ejercicio 2
Tres cajas contienen bolas blancas y negras. La composición de cada una de ellas es la siguiente: U1 = {3B, 1N}, U2 = {2B, 2N}, U3 = {1B, 3N}.
Se elige al azar una de las cajas y se extrae de ella una bola al azar la cual resulta ser blanca. ¿Cuál es la caja con mayor probabilidad de haber sido elegida?
Solución
Mediante U1, U2 y U3, representaremos también la caja elegida.
Estos sucesos constituyen una partición de S y se verifica que P(U1) = P(U2) = P(U3) = 1/3 ya que que la elección de la caja es al azar.
Si B={la bola extraída es blanca}, tendremos P(B|U1) = 3/4 , P(B|U2) = 2/4 , P(B|U3) = 1/4 .
Lo que deseamos obtener es la probabilidad de que la bola haya sido sacada de la caja Ui sabiendo que dicha bola fue blanca, es decir, P(Ui |B), y ver cuál de los tres valores fue el más alto para conocer de cuál caja ha sido más probable la extracción de la bola blanca.
Aplicando el teorema de Bayes a la primera de las cajas:
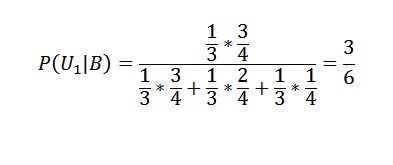
Y para las otras dos:
P(U2|B) = 2/6 y P(U3|B) = 1/6.
Luego, la primera de las cajas es la que tiene una mayor probabilidad de haber sido elegida para la extracción de la bola blanca.
