Producto cruz: qué es, propiedades, ejemplo, ejercicio resuelto
¿Qué es el producto cruz o producto vectorial?
El producto cruz, también llamado producto vectorial, es un tipo de producto que se lleva a cabo entre dos vectores y da como resultado otro vector, perpendicular al plano definido por los dos primeros.
El producto cruz entre dos vectores cualesquiera a y b, da como resultado otro vector R, matemáticamente se escribe de la siguiente forma:
a × b = R
Se lee así: “a cruz b igual a R”.
En texto impreso, los vectores se escriben con letra negrita, o con una flecha encima de la letra, para distinguirlos de su magnitud o módulo. Para este se emplean, indistintamente, las barras de módulo y las letras corrientes, así se tiene que el valor absoluto del vector a simbólicamente se escribe así:
│a│= a
El valor absoluto o módulo del producto vectorial entre dos vectores se calcula multiplicando el módulo de ambos vectores por el seno del ángulo θ que hay entre ellos:
R = a∙b∙sen θ
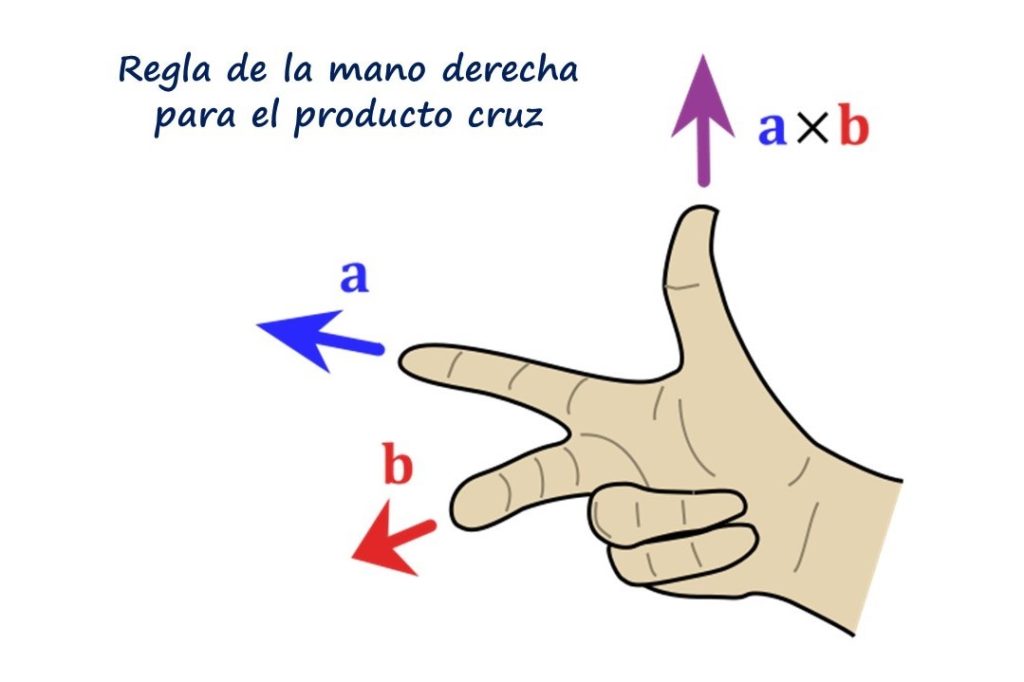
La dirección del vector R es perpendicular a la de los vectores a y b. El sentido de R es dextrógiro de a hacia b y en la práctica se determina usando la regla de la mano derecha, que consiste en posicionar los dedos índice, medio y pulgar de la mano derecha así:
- Se coloca el dedo índice siguiendo al vector a
- Con el dedo medio se sigue al vector b
- El dedo pulgar, extendido, señala la dirección y el sentido del vector R.
Este orden se debe seguir exactamente, pues el producto vectorial no es conmutativo, es decir a × b ≠ b × a y si se intercambian los vectores, no se obtendrá el resultado correcto.
Se aconseja al lector colocar su mano derecha tal como muestra la figura, el índice apuntando a la izquierda representa al vector a, el dedo medio sigue a b y apunta directamente hacia el lector, finalmente, el pulgar señala hacia arriba, señalando dirección y sentido del vector a × b = R.
Propiedades del producto cruz
-El producto cruz o vectorial entre dos vectores siempre resulta en otro vector.
-Un producto cruz no es conmutativo, por lo tanto: a × b ≠ b × a.
-Para el producto cruz se cumple que: a × b = − (b × a). A esta propiedad se la llama anti-conmutatividad.
-El vector resultante del producto vectorial entre dos vectores es perpendicular (normal) a dichos vectores.
-De lo anterior se deduce que el producto vectorial entre vectores con la misma dirección es nulo. En particular a × a = 0.
-El producto cruz cumple la ley distrbutiva respecto a la suma: a × (b+c) = a × b + a × c
-Si m es un escalar, entonces m (a × b) = m a × b = a × m b
Producto cruz entre vectores unitarios
Los tres vectores unitarios, llamados i, j y k, son perpendiculares entre sí y señalan las tres direcciones notables del espacio: alto, ancho y profundidad. Dichas direcciones son perpendiculares entre sí.
El producto vectorial entre los vectores unitarios se determina fácilmente a través de la regla de la mano derecha y teniendo presente las propiedades del producto cruz:
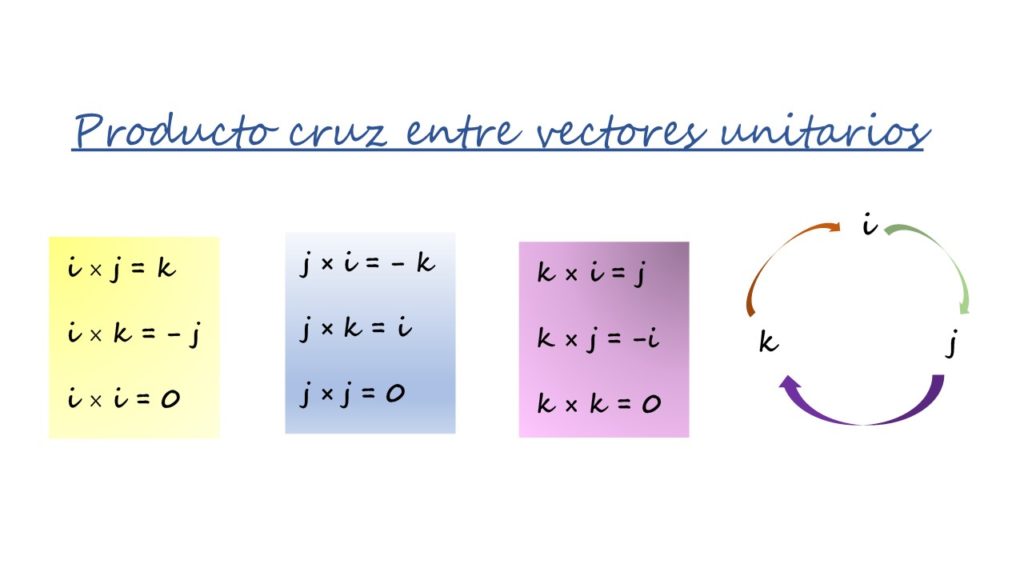
Los tres recuadros de color en la figura, se resumen en el redondel con flechas a la derecha y se usa de esta forma:
-Cuando se multiplica en el sentido de la flecha el resultado es el vector frente a la flecha y tiene signo positivo. Por ejemplo, al multiplicar vectorialmente j y k, el tercer vector es i, y como el orden sigue el sentido de la flecha, el signo es +.
-Y si se multiplica en sentido contrario a la flecha, el resultado es el tercer vector frente a la flecha, pero con signo negativo.
Los vectores unitarios constituyen una base, por lo que cualquier otro vector se puede escribir en términos de ellos. Esto facilita mucho el cálculo del producto cruz entre dos vectores arbitrarios en el espacio.
Cómo calcular analíticamente el producto cruz de dos vectores
Cuando los vectores a y b tienen una dirección arbitraria en el espacio, con componentes a lo largo de cada una de ellas, es más sencillo calcular el producto cruz en forma analítica, expresándolos en términos de los vectores unitarios i, j y k:
- a = axi + ayj + azk
- b = bxi + byj + bzk
Ahora se hace uso de la propiedad distributiva de la multiplicación, la cual es válida también para el producto cruz:
a × b = (axi + ayj + azk) × (bxi + byj + bzk) =
= (axi × bxi) + (axi × byj) + (axi × bzk) + (aYj × bxi) + (aYj × byj) + (aYj × bzk) + (aZk × bxi) + (aZk × byj) + (aZk × bzk)
Los productos cruz entre vectores unitarios iguales se cancelan, por ser vectores paralelos entre sí, lo cual reduce esta expresión a 6 términos:
a × b = (axi × byj) + (axi × bzk) + (aYj × bxi) + (aYj × bzk) + (aZk × bxi) + (aZk × byj)
Por último, empleando la figura de arriba, cada producto da como resultado:
a × b = ax byk + ax bz (−j) + aY bx (−k) + aY bzi + aZ bxj + aZ by (−i) =
= (aY bz − aZ by) i + (aZ bx − ax bz) j + (ax by − aY bx) k
Producto cruz a través de un determinante
No es necesario memorizar la fórmula de arriba, sino aplicar convenientemente el redondel de la figura precedente o simplemente efectuar cuidadosamente el determinante mostrado a continuación, que es totalmente equivalente:
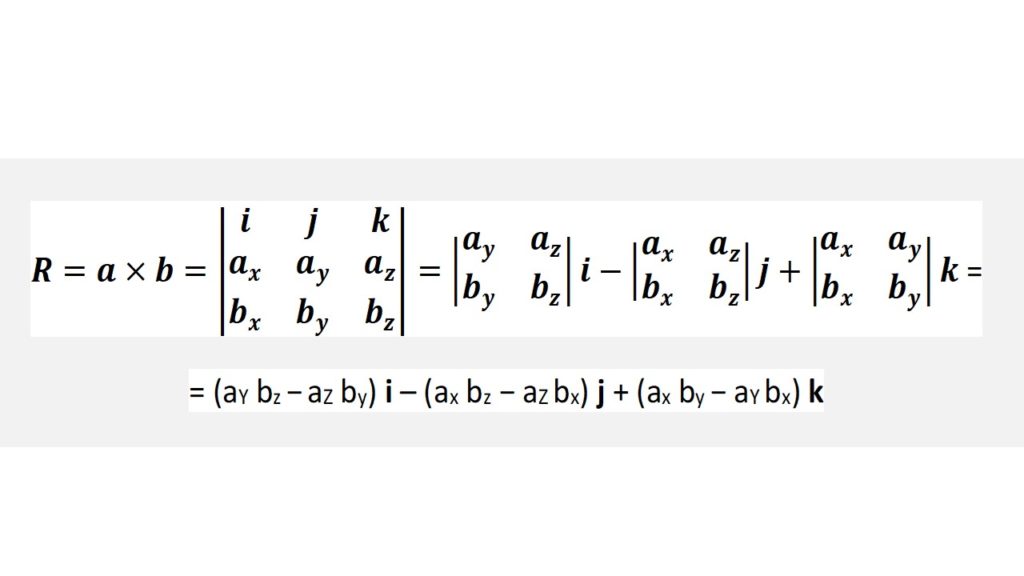
Ejemplo
Suponiendo que los vectores a y b son:
- a = 5 i − j + 4 k
- b = −i + 0j +7 k
El producto cruz entre ellos se calcula identificando y sustituyendo las coordenadas respectivas:
ax = 5; ay = −1; az = 4; bx = −1; by = 0: bz = 7
a × b = [(−1) ∙ 7 – 4 ∙ 0] i + [ (4 ∙ (−1) − 5 ∙ 7) j + [5∙0 − (−1) ∙ (−1)] k = [−7 – 0] i + [ (−4 − 35) j + [0 − 1] k =
= (−7) i − 39 j – k
El método del determinante ofrece el mismo resultado.
Ejercicio
Calcular mediante determinantes, el producto cruz entre los vectores:
- u = 2 i +j + 5 k
- v = i + 4j +7 k
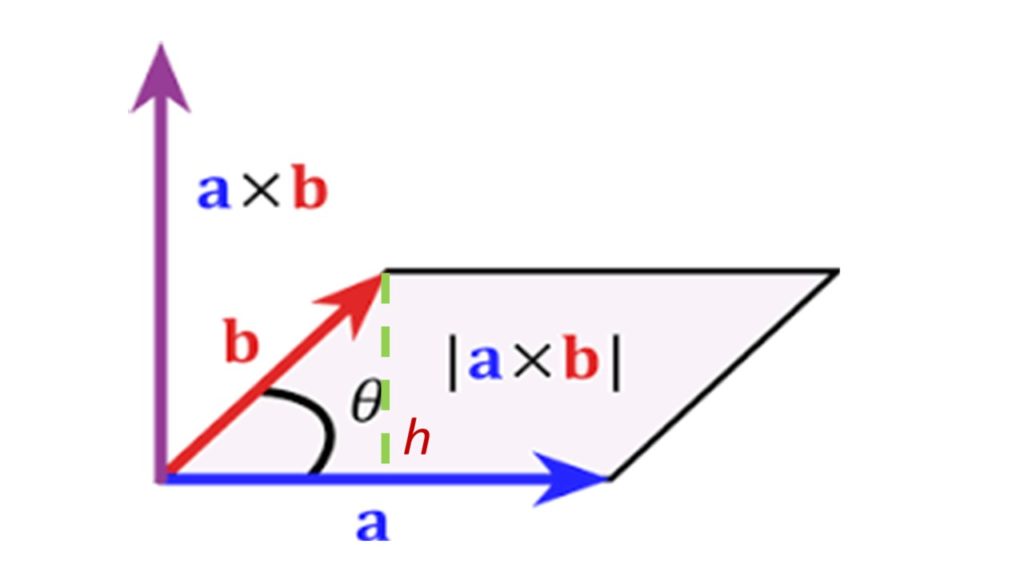
Y determinar el área del paralelogramo subtendido por los vectores anteriores, según se muestra en la figura:
Solución
Se sustituyen los valores de las coordenadas de los vectores en el determinante:

El área del paralelogramo determinado es el módulo del producto vectorial entre ellos, resultando: R= 17,3 unidades de área.
