Homocedasticidad: qué es, importancia y ejemplos
La homocedasticidad en un modelo estadístico predictivo ocurre si en todos los grupos de datos de una o más observaciones, la varianza del modelo respecto de las variables explicativas (o independientes) se mantiene constante.
Un modelo de regresión puede ser homocedástico o no, en cuyo caso se habla de heterocedasticidad.
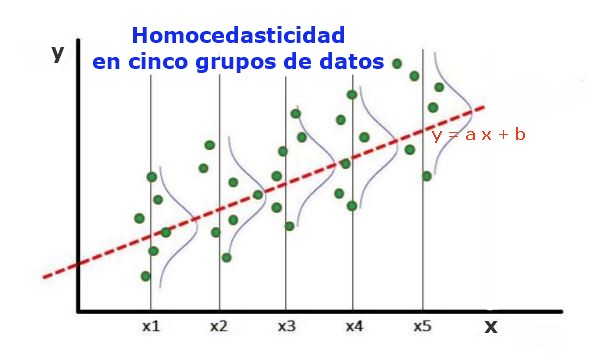
Un modelo estadístico de regresión de varias variables independientes se llama homocedástico, solo si la varianza del error de la variable predicha (o la desviación estándar de la variable dependiente) se mantiene uniforme para diferentes grupos valores de las variables explicativas o independientes.
En los cinco grupos de datos de la figura 1, se ha calculado la varianza en cada grupo, respecto del valor estimado por la regresión, resultando ser igual en cada grupo. Se supone además que los datos siguen la distribución normal.
A nivel gráfico significa que los puntos están igualmente dispersos o desparramados en torno al valor predicho por el ajuste de regresión, y que el modelo de regresión tiene el mismo error y validez para el rango de la variable explicativa.
Índice del artículo
Para ilustrar la importancia de la homocedasticidad en estadística predictiva, es necesario contrastar con el fenómeno contrario, la heterocedasticidad.
En el caso de la figura 1, en la que hay homocedasticidad se cumple que:
Var((y1-Y1); X1) ≈ Var((y2-Y2); X2) ≈……Var((y4-Y4); X4)
Donde Var((yi-Yi);Xi) representa la varianza, el par (xi, yi) representa un dato del grupo i, mientras que Yi es el valor que predice la regresión para el valor medio Xi del grupo. La varianza de los n datos del grupo i se calcula así:
Var((yi-Yi); Xi) = ∑j (yij – Yi)^2/n
Por el contrario, cuando se produce heterocedasticidad el modelo de regresión puede no ser válido para toda la región en que fue calculado. La figura 2 muestra un ejemplo de esta situación.
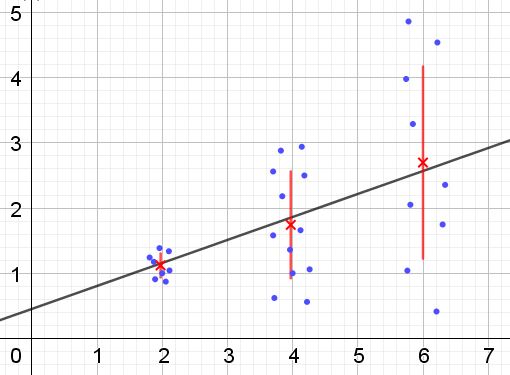
En la figura 2 se representan tres grupos de datos y el ajuste del conjunto mediante una regresión lineal. Debe notarse que los datos en el segundo y en el tercer grupo están más dispersos que en el primer grupo. El gráfico de la figura 2 también muestra el valor medio de cada grupo y su barra de error ±σ, siendo la σ desviación estándar de cada grupo de datos. Debe recordarse que la desviación estándar σ es la raíz cuadrada de la varianza.
Es claro que en el caso de la heterocedasticidad, el error de la estimación por regresión es cambiante en el rango de valores de la variable explicativa o independiente, y en los intervalos donde este error es muy grande, la predicción por regresión es poco confiable o no aplicable.
En un modelo de regresión los errores o residuos (y -Y) deben distribuirse con igual varianza (σ^2) en todo el intervalo de valores de la variable independiente. Es por esta razón que un buen modelo de regresión (lineal o no lineal) debe pasar la prueba de homocedasticidad.
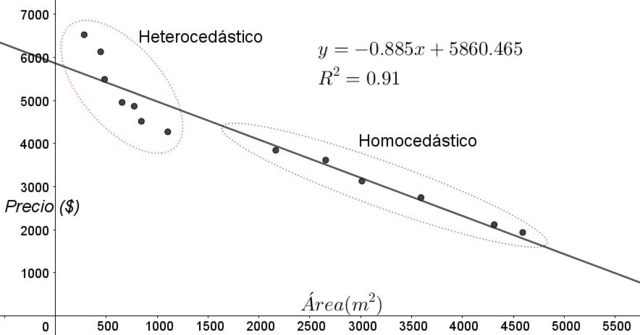
Los puntos que se muestran en la figura 3 corresponden a los datos de un estudio que busca una relación entre los precios (en dólares) de las viviendas en función del tamaño o área en metros cuadrados.
El primer modelo que se ensaya es el de una regresión lineal. En primer lugar se nota que el coeficiente de determinación R^2 del ajuste es bastante alto (91%), por lo que puede pensarse que el ajuste es satisfactorio.
Sin embargo del gráfico del ajuste pueden distinguirse claramente dos regiones. Una de ellas, la de la derecha encerrada en un óvalo, cumple homocedasticidad, mientras que la región de la izquierda no tiene homocedasticidad.
Esto significa que la predicción del modelo de regresión es adecuada y confiable en el rango comprendido entre 1800 m^2 a 4800 m^2 pero muy inadecuada fuera de esta región. En la zona heterocedástica no solo el error es muy grande, sino que además los datos parecen seguir otra tendencia diferente a la propuesta por el modelo de regresión lineal.
El gráfico de dispersión de los datos es la prueba más simple y visual de la homocedasticidad de los mismos, sin embargo en ocasiones donde no es tan evidente como en el ejemplo mostrado en la figura 3, es necesario recurrir a gráficos con variables auxiliares.
Con el propósito de separar las zonas donde se cumple la homocedasticidad y en las que no, se introducen las variables estandarizadas ZRes y ZPred:
ZRes = Abs(y – Y)/σ
ZPred = Y/σ
Debe notarse que estas variables dependen del modelo de regresión aplicado, ya que Y es el valor de la predicción por regresión. A continuación se presenta el gráfico de dispersión ZRes vs ZPred para el mismo ejemplo:
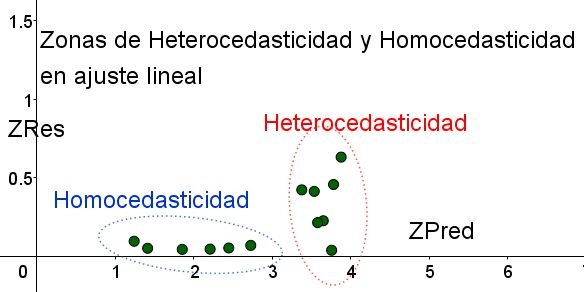
En el gráfico de la figura 4 con las variables estandarizadas, se separa claramente la zona donde el error residual es pequeño y uniforme, respecto de la que no. En la primera zona se cumple la homocedasticidad mientras que en la región donde el error residual es muy variable y grande se cumple la heterocedasticidad.
Al mismo grupo de datos de la figura 3 se le aplica un ajuste por regresión, en este caso el ajuste es no-lineal, ya que el modelo usado involucra una función potencial. El resultado se muestra en la figura siguiente:
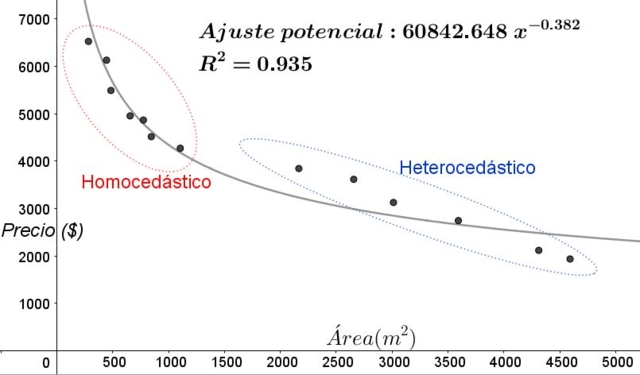
En el gráfico de la figura 5 debe notarse claramente las zonas homocedásticas y heterocedástica. Debe notarse también que estas zonas se intercambiaron respecto a las que se formaban en el modelo de ajuste lineal.
En el gráfico de la figura 5 queda en evidencia que aun cuando se tiene un coeficiente de determinación del ajuste bastante alto (93,5%), el modelo no es adecuado para todo el intervalo de la variable explicativa, ya que los datos para valores mayores a 2000 m^2 presentan heterocedasticidad.
Una de las pruebas no-gráfica más utilizada para verificar si se cumple o no la homocedasticidad es la prueba de Breusch-Pagan.
No se dará en este artículo todos los detalles de esta prueba pero se esboza a grandes rasgos sus características fundamentales y los pasos de la misma:
- Se aplica el modelo de regresión a los n datos y se calcula la varianza de los mismos respecto al valor estimado por el modelo σ^2 = ∑j (yj – Y)^2/n.
- Se define una nueva variable ε = ((yj – Y)^2) / (σ^2)
- Se aplica el mismo modelo de regresión a la nueva variable y se calculan sus nuevos parámetros de la regresión.
- Se determina el valor crítico Chi cuadrado (χ^2), siendo este la mitad de la suma de los cuadrados nuevos residuos en la variable ε.
- Se usa la tabla de la distribución Chi cuadrado considerando en el eje x de la tabla el nivel de significancia (usualmente 5%) y el número de grados de libertad (#de variables de la regresión menos la unidad), para obtener el valor de la tabla.
- Se compara el valor crítico obtenido en el paso 3 con el valor encontrado en la tabla (χ^2).
- Si el valor crítico está por debajo del de la tabla se tiene la hipótesis nula: hay homocedasticidad
- Si el valor crítico está por encima del de la tabla se tiene la hipótesis alternativa: no hay homocedasticidad.
La mayor parte de los paquetes informáticos estadísticos como: SPSS, MiniTab, R, Python Pandas, SAS, StatGraphic y varios otros incorporan la prueba de homocedasticidad de Breusch-Pagan. Otra prueba para verificar uniformidad de varianza el test de Levene.
- Box, Hunter & Hunter. (1988) Estadística para investigadores. Reverté editores.
- Johnston, J (1989). Métodos de econometría, Vicens -Vives editores.
- Murillo y González (2000). Manual de econometría. Universidad de Las Palmas de Gran Canaria. Recuperado de: ulpgc.es.
- Wikipedia. Homocedasticidad. Recuperado de: es.wikipedia.com
- Wikipedia. Homoscedasticity. Recuperado de: en.wikipedia.com
