Ecuaciones de segundo grado: fórmula, cómo resolverlas, ejemplos, ejercicios
Las ecuaciones de segundo grado o cuadráticas y una incógnita tienen la forma ax2 + bx + c = 0. Donde a ≠ 0, ya que de ser 0, la ecuación se transformaría en una ecuación lineal, y los coeficientes a, b y c son números reales.
La incógnita por determinar es el valor de x. Por ejemplo, la ecuación 3x2 – 5x + 2 = 0 es una ecuación completa de segundo grado.
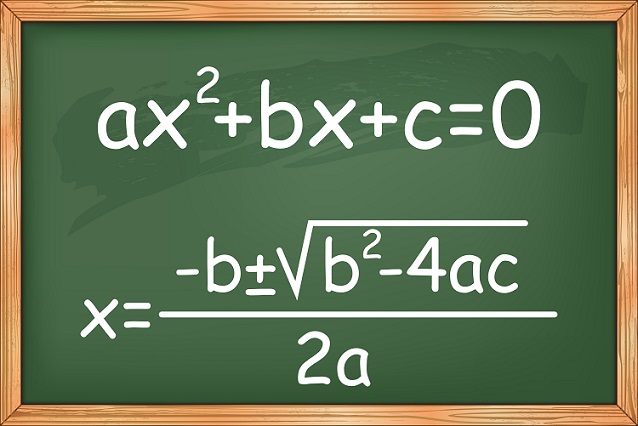
También hay variantes que se conocen como ecuaciones de segundo grado incompletas, las cuales carecen de alguno de los términos, excepto el de ax2. He aquí algunos ejemplos:
x2 – 25 = 0
3x2 – 5x = 0
Al Juarismi, el famoso matemático árabe de la antigüedad, describió en sus obras varios tipos de ecuaciones de primer y segundo grado, pero solamente con coeficientes positivos. Sin embargo, fue el matemático francés Francois Viete quien introdujo por vez primera las letras para simbolizar cantidades y plantear la solución a través de la fórmula resolvente:
Esta es una fórmula de carácter general que permite resolver una ecuación cuadrática, hallando las raíces o ceros de la misma, aun si las soluciones no son reales. Además existen otras formas de resolverlas.
Índice del artículo
- 1 ¿Cómo resolver ecuaciones de segundo grado?
- 2 Ejemplos de ecuaciones de segundo grado sencillas
- 3 Ejercicios resueltos sencillos
- 4 Referencias
Las ecuaciones de segundo grado se pueden resolver mediante la fórmula dada anteriormente, y también existen otros procedimientos algebraicos que pueden dar resultado en algunas ecuaciones.
Vamos a resolver la ecuación propuesta al comienzo con la fórmula, un método válido para cualquier ecuación de segundo grado con una incógnita:
3x2 – 5x + 2 = 0
Para utilizar la fórmula correctamente notemos que:
- a es el coeficiente del término con x2
- b es el coeficiente del término lineal
- c es el término independiente.
Vamos a identificarlos de la misma ecuación:
a = 3
b = -5
c = 2
Nótese que el signo que acompaña al coeficiente debe ser tomado en cuenta. Ahora sustituimos estos valores en la fórmula:
En el numerador se encuentra el símbolo de “mas – menos” ±, lo cual nos indica que la cantidad con raíz puede tomarse como positiva y también como negativa. Una ecuación de segundo grado tiene como máximo dos soluciones reales, y este símbolo lo tiene en cuenta.
Llamemos x1 y x2 a estas dos soluciones, entonces:
x1 = (5+1) / 6 = 1
x2 = (5-1) / 6 = 4/6 = 2/3
Algunas ecuaciones de segundo grado consisten en trinomios que se factorizan fácilmente. De ser así, este método es mucho más rápido. Consideremos la ecuación:
x2 + 7x – 18 = 0
La factorización tiene esta forma:
(x + )⋅(x – )
Los espacios en blanco se llenan con dos números que al ser multiplicados den 18, y al ser restados resulten 7. Los signos en los paréntesis se eligen con este criterio:
-En el primer paréntesis se coloca el signo entre el primero y el segundo término.
-Y en el segundo paréntesis va el producto de los signos que se ven.
En cuanto a los números, se tantean fácilmente en este caso: son 9 y 2. El mayor siempre se coloca en el primero de los paréntesis, así:
x2 + 7x – 18 = (x + 9 ). (x – 2)
El lector puede comprobar mediante la propiedad distributiva, que al desarrollar el producto del lado derecho de la igualdad se obtiene el trinomio de la izquierda. Ahora bien, la ecuación se reescribe:
(x + 9)⋅ (x – 2) = 0
Para que se cumpla la igualdad basta con que uno de los dos factores sea cero. Entonces, en el primero tiene que hacerse x1 = -9 o bien puede ser que el segundo factor se anule, en tal caso x2 = 2. Estas son las soluciones de la ecuación.
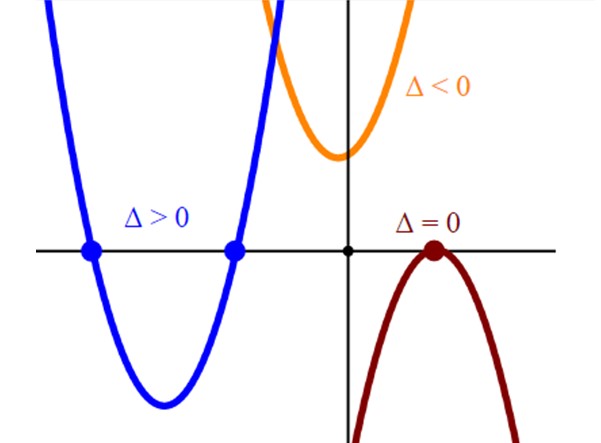
Las raíces o soluciones de la ecuación de segundo grado corresponden a las intersecciones de la parábola y = ax2 + bx + c con el eje horizontal o eje x. De manera que al graficar la parábola correspondiente hallaremos la solución de la ecuación de segundo grado haciendo y = 0.
Los cortes de las parábolas con el eje horizontal representan las soluciones de la ecuación ax2 + bx + c= 0. Una parábola que solamente corte al eje horizontal en un único punto tiene una sola raíz y esta siempre será el vértice de la parábola.
Y por último, si una parábola no corta al eje horizontal, la correspondiente ecuación ax2 + bx + c= 0 carece de soluciones reales.
Construir una gráfica a mano puede resultar laborioso, pero con el uso de programas que grafican en línea es muy sencillo.
Muchos modelos de calculadoras científicas tienen la opción de resolver ecuaciones de segundo grado (y también otros tipos de ecuaciones). Para saberlo hay que revisar el menú.
Una vez que se escoge la opción de ecuación cuadrática de una incógnita, el menú solicita ingresar los valores de los coeficientes a, b y c y retorna las soluciones reales si es que existen. Y también hay modelos de calculadoras científicas que trabajan con números complejos y ofrecen estas soluciones.
Para conocer si la ecuación tiene soluciones reales o no, y cuántas son, sin necesidad de resolver primero, se define el discriminante Δ como la cantidad bajo la raíz cuadrada:
Δ = b2 – 4ac
De acuerdo al signo del discriminante, se sabe cuántas soluciones tiene la ecuación según este criterio:
-Dos soluciones reales: Δ > 0
-Una solución real (o dos soluciones idénticas): Δ = 0
-Sin solución real: Δ 0
Por ejemplo, ¿cuántas soluciones tiene la ecuación de segundo grado -7x2 +12x + 64 = 0? Identificamos los coeficientes:
a = -7
b = 12
c = 64
Δ = b2 – 4ac = 122 – 4x (-7) x 64 = 144 + 1792 = 1936 > 0
La ecuación tiene dos soluciones. Ahora veamos esta otra:
x2 – 6x + 9 = 0
a = 1
b = -6
c = 9
Δ = (-6)2 – 4 x 1 x 9 = 36 – 36 = 0
Esta es una ecuación con solución única o con dos soluciones iguales.
Al comienzo dijimos que las ecuaciones de segundo grado podían ser completas si el trinomio lo está, e incompletas si faltaba el término lineal o el término independiente. Ahora veamos algunos tipos particulares:
En este caso a = 1 y la fórmula se reduce a:
Para este tipo de ecuación, y siempre dependiendo de los restantes coeficientes, puede funcionar bien el método de factorización, tal como vimos en la sección precedente.
La solución, si existe, es de la forma:
Hay solución real cuando a o c tienen signo negativo, pero si los dos términos tienen el mismo signo, la solución será imaginaria.
Esta ecuación se resuelve rápidamente empleando factorización, ya que la x es factor común en ambos términos. Una de las soluciones siempre es x = 0, la otra se halla así:
ax2 + bx = 0
x (ax + b) = 0
ax + b = 0 → x = -b/a
Veamos un ejemplo seguidamente. Resolver:
x2 – 5x = 0
x (x – 5) = 0
Por lo tanto x1 = 0 y x2 = 5
Hay diversas ecuaciones de tipo racional, en las cuales la incógnita puede estar presente tanto en el numerador como en el denominador, o incluso solo en este último, y que mediante manipulaciones algebraicas se reducen a ecuaciones cuadráticas.
La manera de resolverlas es multiplicar ambos lados de la igualdad por el mínimo común múltiplo o m.c.m de los denominadores y luego reacomodar los términos. Por ejemplo:
Hay ecuaciones de orden superior que mediante un cambio de variable, se pueden resolver como si fueran cuadráticas, por ejemplo esta ecuación bicuadrada:
x4 – 10x2 + 9 = 0
Sea x2 = u, entonces la ecuación se transforma en:
u2 – 10u + 9 = 0
Esta ecuación se resuelve rápidamente mediante factorización, encontrando dos números que multiplicados den 9 y sumados 10. Estos números son 9 y 1:
(u – 9).(u – 1) = 0
Por lo tanto las soluciones de esta ecuación son u1 = 9 y u2 = 1. Ahora regresamos el cambio:
x2 = 9 → x1 = 3 y x2 = -3
x2 = 1 → x1 = 1 y x2 = -1
La ecuación original es de orden 4, por lo tanto posee al menos 4 raíces. La del ejemplo son -3, -1, 1 y 3.
Resolver la siguiente ecuación cuadrática con la incógnita en el denominador:
El mínimo común múltiplo es x(x+2) y debe multiplicar a todos los términos:
Queda la expresión equivalente:
5x(x+2) – x = x (x+2)
Desarrollamos:
5x2 + 10x – x = x2 + 2x
Se trasponen todos los términos a la izquierda de la igualdad y a la derecha se deja 0:
5x2 + 10x – x – x2 – 2x = 0
4x2 – 7x = 0
Factorizamos, ya que es una ecuación incompleta:
x(4x – 7) =0
Una de las soluciones es x = 0, la otra es:
4x = 7
x = 7/4
Hallar la solución de las ecuaciones de segundo grado:
a) -7x2 +12x + 64 = 0
b) x2 – 6x + 9 = 0
Solución a
De esta ecuación conocemos el determinante Δ, porque se calculó a modo de ejemplo antes, así que vamos a aprovecharlo, expresando la fórmula resolvente así:
x1 = (-12+44) / -14 = – (32/14) = – (16/7)
x2 = (-12 – 44) / -14 = 4
Solución b
El trinomio cuadrado x2 – 6x + 9 es factorizable, ya que es un trinomio cuadrado perfecto:
x2 – 6x + 9 = (x-3)2 = 0
La solución de esta ecuación es x = 3.
¿Cuál es la ecuación cuyas soluciones son 3 y 4?
Solución
La expresión factorizada es:
(x – 3) ⋅ (x – 4) = 0
Aplicando propiedad distributiva:
x2 – 4x -3x + 12 = 0
Los dos términos centrales son semejantes y se pueden reducir, quedando:
x2 – 7x + 12 = 0
- Baldor. 1977. Álgebra Elemental. Ediciones Cultural Venezolana.
- Hoffman, J. Selección de temas de Matemática. Volumen 2.
- Jiménez, R. 2008. Álgebra. Prentice Hall.
- Stewart, J. 2006. Precálculo: Matemáticas para el Cálculo. 5ta. Edición. Cengage Learning.
- Zapata, F. 4 formas de resolver una ecuación de segundo grado. Recuperado de: francesphysics.blogspot.com.
- Zill, D. 1984. Álgebra y Trigonometría. McGraw Hill.
