Pentadecágono: elementos, clasificación, características, ejercicio
Un pentadecágono es una figura plana construida con quince segmentos rectos y en forma cerrada. A esta clase de figuras se las denomina polígono y se las nombra de acuerdo a la cantidad de lados que tengan.
El triángulo, con tres lados y el cuadrilátero, de cuatro, son ejemplos de polígonos muy familiares, pero los polígonos pueden tener más lados.
Los elementos básicos del pentadecágono son los mismos de cualquier polígono, independientemente de la cantidad de lados que posea. Dichos elementos son:
–Lados, que son los segmentos que conforman el pentadecágono para un total de 15.
–Vértices, también 15, que son los extremos de los lados adyacentes.
–Ángulos internos, los que se forman dentro del pentadecágono entre dos lados adyacentes.
–Ángulos externos, formados entre un lado y la prolongación de uno de los lados consecutivos.
–Diagonales, los segmentos de recta que unen dos vértices no adyacentes.
Índice del artículo
- 1 Clasificación
- 2 El pentadecágono regular
- 3 Construcción con regla y compás
- 4 Ejercicio resuelto
- 5 Referencias
Un pentadecágono puede ser regular o irregular, dependiendo del tamaño de sus lados y la medida de sus ángulos internos. Si tiene todos los lados y los ángulos internos iguales –equilátero y equiángulo- es regular, como el que se muestra en la figura 1, de lo contrario es irregular.
También se puede clasificar como convexo o cóncavo. Un pentadecágono cóncavo tiene uno o más ángulos internos mayores a 180º, en tanto que uno convexo tiene siempre ángulos internos menores que 180º. El pentadecágono regular es convexo.
Otro criterio de clasificación se tiene al considerar si sus lados no consecutivos -o sus prolongaciones- se cortan o no. Cuando no se cortan, como en el caso de la figura 1, se dice que es un pentadecágono simple. Y si se cortan, entonces es complejo.
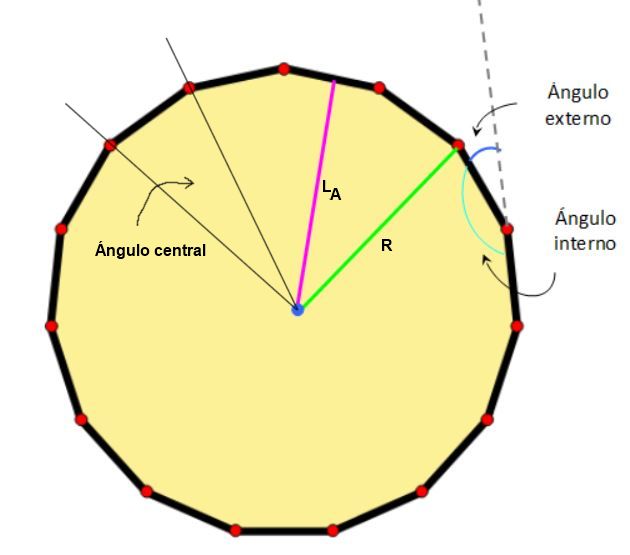
El pentadecágono regular, cuyos lados y ángulos internos tienen la misma medida, es una figura de mucha simetría, por que se definen los siguientes elementos adicionales a los descritos previamente:
–Centro: el punto que equidista de los vértices y los lados.
–Radio: la distancia del centro a uno de los vértices del pentadecágono regular.
–Ángulo central: el que tiene su vértice en el centro de la figura y sus lados pasan por dos vértices adyacentes.
–Apotema, es el segmento perpendicular que une el centro de un lado con el centro de la figura.
Ángulos internos
La siguiente fórmula se utiliza para calcular la medida I de los ángulos internos de cualquier polígono regular, donde n es el número de lados:
En esta fórmula, la medida I viene en grados, para expresarla en radianes se multiplica por el factor π/180. Vamos a ver cuál es la medida de los ángulos internos del pentadecágono regular, sustituyendo n= 15:
I = [(15-2)×180º]/15 = 156º
Que equivale a 13π/15 radianes. Como los ángulos internos del pentadecágono regular son menores de 180º, se trata de un polígono convexo.
Suma de los ángulos internos
Es posible calcular la suma S de los ángulos internos mediante la siguiente fórmula:
S = (n-2) x 180º
Como siempre, n representa el número de lados. Esta fórmula es válida para n = 3, 4, 5 ….
Haciendo n=15 obtenemos:
S = (15 – 2) x 180º = 2340º
Ángulos externos
Un ángulo interno y un ángulo externo son suplementarios, es decir, que su suma es 180º, tal como se advierte de la figura 2. Por lo tanto un ángulo externo del pentadecágono mide:
180 º – 156º = 24º.
Perímetro y área
El perímetro es la medida del contorno del polígono y se encuentra fácilmente sumando todos los lados. Si a es la longitud del lado, basta con multiplicar por n, el número de lados.
Para un pentadecágono regular de lado a, el perímetro P es:
P = 15a
Si se trata de una figura irregular, en la cual la medida de los lados difiere, el perímetro se encuentra sumando la longitud de todos sus lados.
En cuanto al área, podemos calcularla de varias formas. Por ejemplo tenemos la fórmula que permite obtenerla conociendo la longitud a de sus lados:
A = 17,6426⋅a2
Existe otra opción, aplicable a los polígonos regulares. Se trata de dividirlos en triángulos de base igual al lado del polígono a. La altura del triángulo es la longitud de la apotema LA, definida anteriormente.
El área de dicho triángulo se calcula con la conocida fórmula: base x altura /2. De esta manera el área de un solo triángulo es:
Área = a. LA /2
Para tener el área total del polígono basta con multiplicar por el número de lados n, que en este caso es 15:
A = 15⋅a⋅ LA /2
Y dado que el perímetro de la figura es P = 15⋅a, entonces:
A = P⋅ LA /2
Diagonales
Las diagonales son los segmentos que unen dos vértices no consecutivos, como se dijo anteriormente. Para saber cuántas diagonales tiene un polígono regular de n lados, incluyendo al pentadecágono, existe la siguiente fórmula:
Donde D es el número de diagonales.
Ahora sustituimos n = 15, para obtener el total de las diagonales:
D = [15 × (15-3)]/2 = 90 diagonales.
El pentadecágono se construye con regla y compás partiendo de una circunferencia. Los 360º deben dividirse en 15 partes iguales de 24º cada una. Primero se realizan las construcciones auxiliares indicadas en la animación para obtener un ángulo de 60º, que se divide a su vez en 36º y 24º.

Si el perímetro de un pentadecágono inscrito en una circunferencia de radio R es 12,56 cm. Calcular:
a) El radio.
b) Su área.
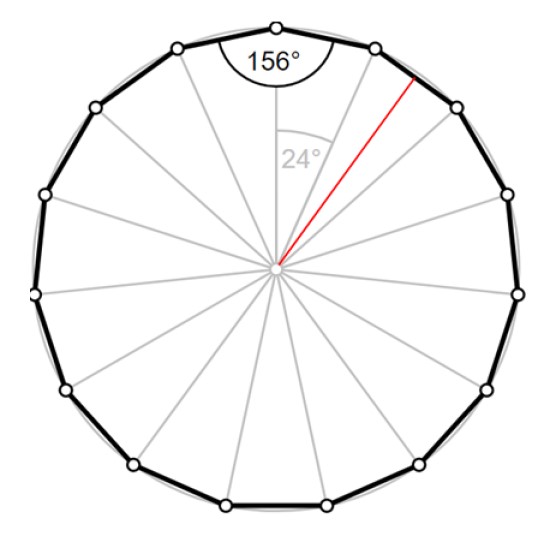
El perímetro es P = 15⋅a = 12.56 cm, por lo tanto el lado del pentadecágono es 0.8373 cm. El radio lo podemos calcular con ayuda de uno de los triángulos de la figura 4.
La apotema LA corresponde a la altura del triángulo, dibujada en rojo, que divide al ángulo de 24º en dos ángulos de 12º cada uno.
Quedan dos triángulos rectángulos con un ángulo interno de 12º cada uno, y a cualquiera de ellos podemos aplicarle trigonometría para encontrar la hipotenusa, que es la longitud R del radio.
De esta manera:
sen 12º = (a/2) /R
R = (a/2) /sen 12º = (0.8373 cm /2) / sen12º = 2.01 cm.
Podemos calcular el área del pentadecágono mediante la fórmula:
A = P⋅ LA /2
Ya conocemos el perímetro P = 12.56 cm, y la longitud de la apotema se calcula mediante la tangente o el coseno de 12º:
cos 12º = LA / R
LA = R. cos 12 º = 2.01 cm. cos 12 º = 1.97 cm
Sustituyendo:
A = 12.56 cm⋅ 1.97 cm /2 = 12.35 cm2
- Alexander, D. 2013. Geometría. 5ta. Edición. Cengage Learning.
- Aprende Matemática. Figuras geométricas. Recuperado de: rodrigoanchorena.wixsite.com.
- Sangaku Maths. Elementos de un polígono y su clasificación. Recuperado de: sangakoo.com.
- Wikipedia. Pentadecágono. Recuperado de: es.wikipedia.org.
- Wolfram Math World. Pentadecagon. Recuperado de: mathworld.wolfram.com.
