Regla de Sarrus
La regla de Sarrus se usa para calcular el resultado de determinantes de 3×3. Estos se emplean para resolver ecuaciones lineales y saber si son compatibles.
Los sistemas compatibles permiten obtener la solución más fácilmente. También se utilizan para determinar si conjuntos de vectores son linealmente independientes y formar la base del espacio vectorial.
Estas aplicaciones se basan en la invertibilidad de las matrices. Si una matriz es regular, su determinante es distinto de 0. Si es singular, su determinante vale 0. Los determinantes sólo se pueden calcular en matrices cuadradas.
Para calcular matrices de cualquier orden, se puede utilizar el teorema de Laplace. Este teorema nos permite simplificar las matrices de dimensiones altas, en sumas de pequeños determinantes que descomponemos de la matriz principal.
Afirma que el determinante de una matriz es igual a la suma de los productos de cada renglón o columna, por la determinante de su matriz adjunta.
Esto va reduciendo los determinantes de manera que un determinante de grado n, se convierte en n determinantes de n-1. Si aplicamos esta regla de forma sucesiva, podemos llegar a obtener determinantes de dimensión 2 (2×2) o 3 (3×3), donde resulta mucho más fácil su cálculo.
Regla de Sarrus
Pierre Frederic Sarrus fue un matemático francés del siglo XIX. La mayoría de sus tratados matemáticos se basan en métodos de resolución de ecuaciones y el cálculo de variaciones, dentro de las ecuaciones numéricas.
En uno de sus tratados, resolvió uno de los enigmas más complejos de la mecánica. Para resolver los problemas de las piezas articuladas, Sarrus introdujo la transformación de movimientos rectilíneos alternativos, en movimientos circulares uniformes. A este nuevo sistema se le conoce como el mecanismo de Sarrus.
La investigación que más fama le dio a este matemático fue en la que introdujo un nuevo método de cálculo de determinantes, en el artículo “Nouvelles méthodes pour la résolution des équations” (Nuevo método para la resolución de ecuaciones), que fue publicado en el año 1833. Este modo de resolver ecuaciones lineales, se conoce como regla de Sarrus.
La regla de Sarrus permite calcular el determinante de una matriz de 3×3, sin necesidad de utilizar el teorema de Laplace, introduciendo un método mucho más sencillo e intuitivo. Para poder comprobar el valor de la regla de Sarrus, tomamos una matriz cualquiera de dimensión 3:
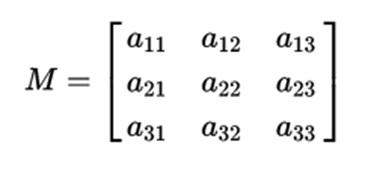
El cálculo de su determinante se realizaría mediante el producto de sus diagonales principales, restándole el producto de las diagonales inversas. Esto quedaría de la siguiente manera:
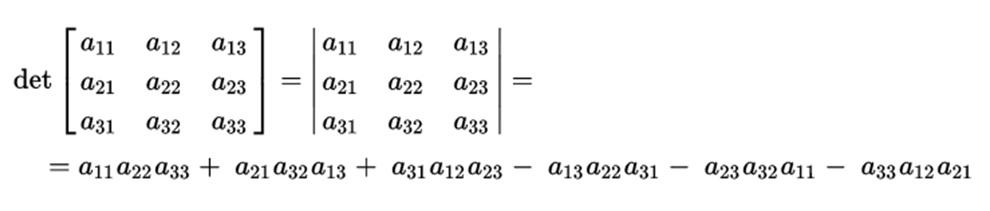
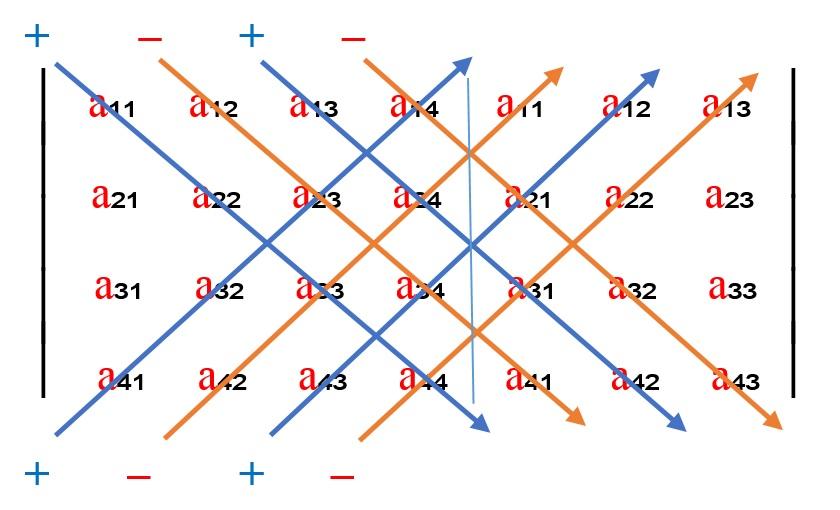
La regla de Sarrus nos permite obtener una visión mucho más sencilla a la hora de calcular las diagonales del determinante. Se simplificaría añadiendo las dos primeras columnas a la parte posterior de la matriz. De esta manera, se ve más claramente cuáles son sus diagonales principales y cuáles las inversas, para el cálculo del producto.
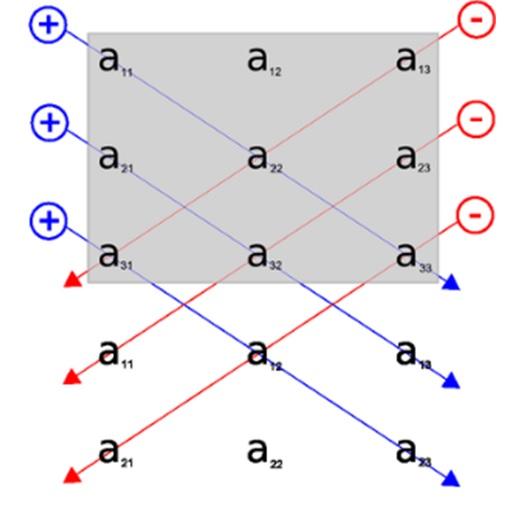
A través de esta imagen podemos ver la aplicación de la regla de Sarrus, incluimos la fila 1 y 2, debajo de la representación gráfica de la matriz inicial. De esta manera, las diagonales principales, son las tres diagonales que aparecen en primer lugar.
Las tres diagonales inversas, a su vez, son aquellas que aparecen en primer lugar en la parte posterior.
De esta manera, las diagonales aparecen de una manera más visual, sin complicar la resolución del determinante, tratando de averiguar que elementos de la matriz pertenecen a cada diagonal.
Como aparece en la imagen, elegimos las diagonales y calculamos el producto resultante de cada función. Las diagonales que aparecen en azul son aquellas que se suman. A la suma de estas, le restamos el valor de las diagonales que aparecen en rojo.
Para que la compresión sea más fácil, podemos utilizar un ejemplo numérico, en vez de utilizar términos y subtérminos algebraicos.
Si tomamos una matriz 3×3 cualquiera, por ejemplo:
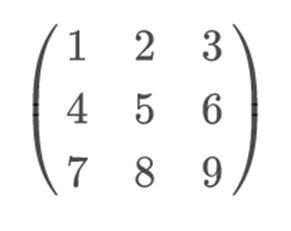
Para aplicar la regla de Sarrus, y resolverla de un modo más visual, deberíamos incluir la fila 1 y 2, como fila 4 y 5 respectivamente. Es importante mantener la fila 1 en la 4ª posición, y la fila 2 en la 5ª. Ya que si las intercambiamos, la Regla de Sarrus no resultará efectiva.
Para calcular el determinante, nuestra matriz quedaría de la siguiente forma:
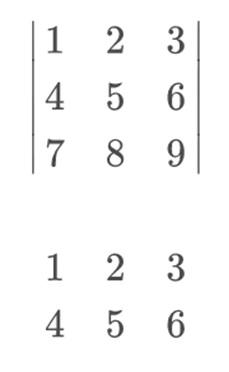
Para seguir con el cálculo, multiplicaremos los elementos de las diagonales principales. Las descendentes que empiezan por la izquierda, llevarán signo positivo; mientras que las diagonales inversas, que son las que comienzan por la derecha, llevan un signo negativo.
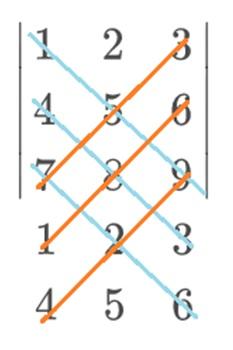
En este ejemplo, las azules irían con signo positivo y las rojas con signo negativo. El cálculo final de la Regla de Sarrus quedaría de esta manera:
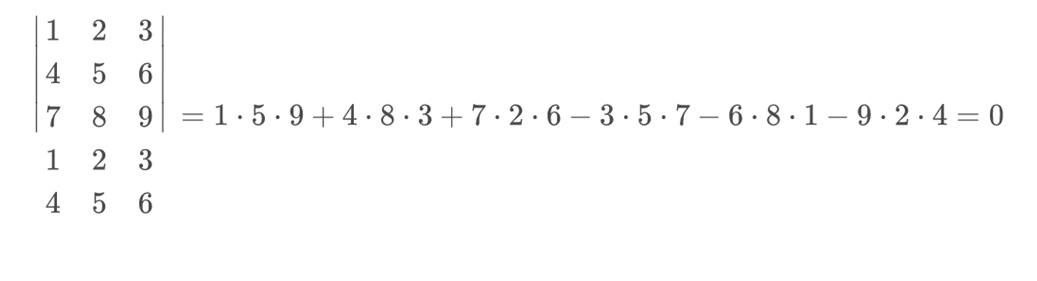
Tipos de determinantes
Determinante de dimensión 1
Si la dimensión de la matriz es 1, la matriz es de ésta forma: A=(a)
Por lo tanto, su determinante quedaría de la siguiente manera: det(A)= |A|=a
De manera resumida, el determinante de la matriz A, es igual al valor absoluto de la matriz A, que en este caso es a.
Determinante de dimensión 2
Si pasamos a las matrices de dimensión 2, obtenemos matrices del tipo:

Donde su determinante se define como:
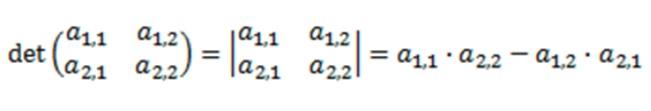
La resolución de este determinante se basa en la multiplicación de su diagonal principal, restando el producto de su diagonal inversa.
Como regla mnemotécnica, podemos utilizar el siguiente diagrama para recordar su determinante:
Determinante de dimensión 3
Si la dimensión de la matriz es 3, la matriz resultante sería de este tipo:
El determinante de esta matriz se resolvería a través de la regla de Sarrus de esta manera:
Referencias
- Jenny Olive (1998) Maths: A Student’s Survival Guide. Cambridge University Press.
- Richard J. Brown (2012) 30-Second Maths: The 50 Most Mind-Expanding Theories in Mathematics. Ivy Press Limited.
- Dave Kirkby (2004) Maths Connect. Heinemann.
- Awol Assen (2013) A Study on the Computation of the Determinants of a 3×3 Matrix. Lap Lambert Academic Publishing.
- Anthony Nicolaides (1994) Determinants & Matrices. Pass Publication.
- Jesse Russell (2012) Rule of Sarrus.
- M. Casteleiro Villalba (2004) Introducción al álgebra lineal. ESIC Editorial.
